5.4 Binomial Distribution

In engineering and science, decisions often hinge on understanding and managing risks. At a manufacturing plant, for example, there will be a percentage of parts that are defective in a shipment. The recipient has to decide whether to accept the shipment, even if every part cannot be tested to see if it is defective or not. For situations with only two possible outcomes, such as success or failure, there is a way to quantify how many defective items are expected and minimize risk and loss. Such situations are called binomial and future outcomes can be predicted using the binomial probability distribution. With it, engineers can assess the likelihood of different quality outcomes, use data to optimize manufacturing processes, and make informed decisions regarding quality control measures.

What Constitutes a Binomial Experiment?

There are several characteristics of a binomial experiment.

  1. There are a fixed number of trials. Think of trials as repetitions of an experiment. The letter n denotes the number of trials.
  2. There are only two possible outcomes. In a trial we classify the two outcomes as “success” and “failure”. The letter p typically denotes the probability of a success on one trial, and q denotes the probability of a failure on one trial, so p+q = 1.
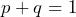  3. The n trials are independent and are repeated using identical conditions.
  4. The probability of a success does not change from trial to trial. Because the n trials are independent, the outcome of one trial does not help in predicting the outcome of another trial. Another way of saying this is that for each individual trial, the probability, p, of a success and probability, q, of a failure remain the same.

Any experiment that has these characteristics but where n = 1 is called a Bernoulli Trial, which has been discussed previously. When we count the successes of repeated independent Bernoulli trials, we form a new random variable, Y, made up of the sum of identical Bernoulli trials, each with the same probability of success, p.

If each X_{i} \sim \text{Bernoulli}(p), then Y = X_{1} + X_{2} + . . . + X_{n} and Y is a binomial random variable.

\mu_{Y} = \mu_{X_{1}} + \mu_{X_{2}} + \mu_{X_{3}} + . . . + \mu_{X_{n}} = np.

\sigma^2_{Y} = \sigma^2_{X_{1}} + \sigma^2_{X_{2}} + \sigma^2_{X_{3}} + . . . + \sigma^2_{X_{n}} = np(1-p) = npq

\sigma_{Y} = \sqrt{\sigma_{X_{1}} + \sigma_{X_{2}} + \sigma_{X_{3}} + . . . + \sigma_{X_{n}}} = \sqrt{np(1-p)} = \sqrt{npq}

Binomial Probability Distribution

When the outcomes of an experiment are binomial and the random variable X = the number of successes obtained in n independent trials, then the random variable has a Binomial Probability Distribution and we write,  X ~ Bin(n, p).

X is a discrete random variable and it can take on the values 0, 1, 2, …, n.

The mean {\mu_X = np.}

The variance { \sigma^2_X = npq. }

The standard deviation { \sigma_X = \sqrt{npq}}.

Example 1 – True/False Questions on an Exam

A student randomly guesses the answers for each of the 10 true-false question on an exam. If a success is defined as guessing correctly, then a failure is guessing incorrectly. Suppose the student guesses correctly on any true-false question 60% of the time. This qualifies as a binomial experiment, so give the probability of a success, probability of a failure, and the value of n. Describe the random variable, its distribution, and the values it can take on. What is the mean and standard deviation of this binomial random variable?

Answers:

The probability of a success is p = 0.6, so the probability of a failure is q = 0.4. There are ten questions so n = 10. The random variable X represents the number of successes, which in this case is the number of correctly answered questions. Therefore, X ~ Bin(10, 0.6) and the random variable X can take on the values of 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, and 10.

The mean of the Binomial distribution is \mu_X=(10)(0.6) = 6 correct answers and the standard deviation is \sigma_X = \sqrt{npq} = \sqrt{(10)(0.6)(0.4)} = 2.4 correct answers.

Notice that a requirement of independence exists for each Bernoulli trial, so that the probability of a success is unaffected by previous trials. Suppose we have a finite population and we take a sample and classify each sampled item as acceptable or defective. As long as the population is large compared to the sample size, we can assume that the trials are independent enough, so the total number of acceptable items has a binomial distribution. If the population size is not large compared to the sample size, then the Bernoulli trials would not be independent and the number of acceptable items would not have a binomial distribution. When we classify a scenario as a particular type of experiment, all of the assumptions must be assessed and met. A generally accepted rule of thumb is that as long as the sample size is at most 5% of the population, then a binomial distribution may be used.

Example 2 – Game with Two Outcomes

Suppose you play a game that you can only either win or lose, so no ties are allowed. The probability that you win any game is 55%, and the probability that you lose is 45%. Each game you play is independent. If you play the game 3 times, let’s calculate the probability you win twice and use the calculations to help us generalize the probability calculations for binomial random variables.

Answer:
If we define X as the number of wins, then X  can take on the values 0, 1, 2, and 3. The probability of a success is p = 0.55. The probability of a failure is q = 0.45. The number of trials is n = 3.

There are three ways to arrange two wins in three plays: WWL, WLW, and LWW.

Let’s calculate the probability of each arrangement.

P(WWL) = (0.55)(0.55)(0.45) = (0.55)2(0.45)1

P(WLW) = (0.55)(0.45)(0.55) = (0.55)2(0.45)1

P(LWW) = (0.45)(0.55)(0.55) = (0.55)2(0.45)1

Notice each outcome had the same probability, so we can say

P(X = 2) = P(WWL) + P(WLW) + P(LWW) = 3(0.55)2(0.45)1

Examine that expression closely. The number 3 is the number of arrangements of two successes (wins) and one failure (loss). Notice the probability of a success, 0.55, has an exponent of 2 for the two wins in each calculation and the probability of a failure, 0.45, has an exponent of 1 for the one loss in each calculation. We need a general way of expressing the number of arrangements of x successes in n trials. This formula will be provided without proof and is \frac{n!}{x!(n-x)!} .

Notice in this case that calculation becomes \frac{3!}{2!(3-2)!} = \frac{(3)(2)(1)}{(2)(1)(1)} = 3.

We can now generalize the calculation from Example 2 to create the binomial probability distribution.

Binomial Probability Density Function

If the random variable X has a binomial distribution we say $latex X \sim $ Bin(n, p).

P(X = x) = 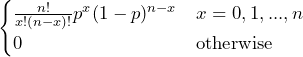\begin{cases}\frac{n!}{x!(n - x)!}p^x(1-p)^{n-x} & x = 0, 1, ..., n\\0 & \text{otherwise}\end{cases}

Read this as “X  is a random variable with a binomial distribution.” The parameters of a binomial probability distribution are n and p, where  n = number of trials and p = probability of a success on each trial.

Example 3 – Using the Binomial Probability Density Function

A trainer is teaching a dolphin to do tricks. The probability that the dolphin successfully performs the trick is 35%. Calculate the probability the dolphin will be successful 12 out of the 20 attempts.

Answer: Let X represent the number of times the dolphin successfully performs the trick. We want to find P(X = 12), when we know n = 20, p = 0.35, and q = 0.65.

P(X=12) = \frac{20!}{12!(20 - 12)!}(0.35)^{12} (0.65)^8 \approx 0.01356. The dolphin will be successful 12 out of 20 attempts approximately 1.4% of the time.

Example 4 – Using the Binomial Probability Density Function

A fair coin is flipped 15 times. Each flip is independent. What is the probability of getting more than ten heads?

Answer: Let X = the number of heads in 15 flips of the fair coin. X  takes on the values 0, 1, 2, 3, …, 15. Since the coin is fair, p = 0.5 and q = 0.5. The number of trials is n = 15.

(1)   \begin{align*} P(X > 10) & = P(X = 11) + P(X = 12) + P(X = 13) + P(X = 14) + P(X = 15) \\ &= \frac{15!}{11!(15 - 11)!}(0.5)^{11}(0.5)^{4} + \frac{15!}{12!(15 - 12)!}(0.5)^{12}(0.5)^{3} \\ &+ \frac{15!}{13!(15 - 13)!}(0.5)^{13}(0.5)^{2} + \frac{15!}{14!(15 - 14)!}(0.5)^{14}(0.5)^{1} \\ &+ \frac{15!}{15!(15 - 15)!}(0.5)^{15}(0.5)^{0} \\ &\approx 0.05932 \end{align*}

.

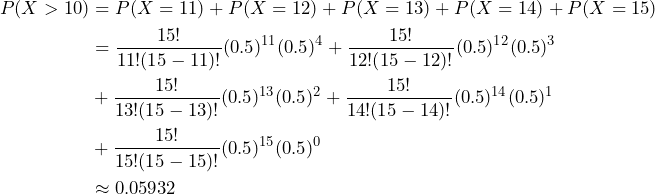
Therefore approximately 6% of the time, we would expect to observe more than ten heads in 15 flips of a fair coin.

Notice that many calculations had to be done in Example 4 because we had to add up five different calculations based on the binomial probability density function. When dealing with the idea of finding probabilities related to more than a specific number or less than a specific number, it is sometimes more convenient to think about the complementary event. The next example demonstrates this idea.

Example 5 – Probability of a Complementary Event

A fair, six-sided die is rolled ten times. Each roll is independent. You want to find the probability of rolling a 1 at least three times. State the probability question mathematically and then calculate the probability.

Answer: At least three times means P(X ≥ 3) = P(X = 3) + P(X = 4) + P(X = 5) + P(X = 6) + P(X = 7) +P(X = 8) + P(X = 9) + P(X = 10).

One way to calculate this is by finding the probability of the complementary event, P(X ≤ 2), then subtracting from 1.

(2)   \begin{align*} P(X\geq 3) &= 1 - P(X \leq 2) \\ &= 1 -\left[P(X=0) + P(X=1) + P(X=2) \right] \\ &= 1 - \left[\frac{10!}{0!(10-0)!}\left(\frac{1}{6}\right)^0 \left(\frac{5}{6}\right)^{10} + \frac{10!}{1!(10-1)!}\left(\frac{1}{6}\right)^1 \left(\frac{5}{6}\right)^9 + \frac{10!}{2!(10-2)!}\left(\frac{1}{6}\right)^2 \left(\frac{5}{6}\right)^8 \right] \\ &= 1 - 0.77523 \\ &= 0.22478 \end{align*}

You will expect to roll a 1 at least three times about 22.5% of the time.

 

 

Example 6 — Application of a Binomial Random Variable

In a certain region of the country 41% of adult workers have a high school diploma and do not pursue any further education. If 20 adult workers are randomly selected from the region, find the probability that at most 3 of them have a high school diploma and do not pursue any further education. How many adult workers do you expect to have a high school diploma and not pursue any further education?

Answer: Let X = the number of workers who have a high school diploma and do not pursue any further education.

X takes on the values 0, 1, 2, …, 20 where n = 20, p = 0.41, and q = 1 – 0.41 = 0.59.

X \sim \text{Bin}(20, 0.41)

We are asked to find P(X ≤ 3), which can be computed using P(X = 0) + P(X = 1) + P(X = 2) + P(X = 3)

(3)   \begin{align*} P(X \leq 3) &= \frac{20!}{0!(20 - 0)!}(0.41)^{0}(0.59)^{3} + \frac{20!}{1!(20 - 1)!}(0.41)^{1}(0.59)^{2} \\ &+ \frac{20!}{2!(20 - 2)!}(0.41)^{2}(0.59)^{1} + \frac{20!}{3!(20 - 3)!}(0.41)^{3}(0.59)^{0} \\ &\approx 0.01278 \end{align*}

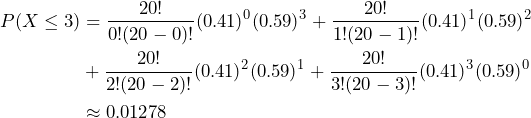
Note

The probability that at most 3 workers have a high school diploma and do not pursue any further education is approximately 1.3%.

The probability density function for this random variable is shown below.

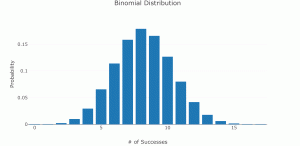
histogram shows binomial distribution where n is 20 and p is 0.41.

The vertical axis shows the probability of X taking on a particular value, x, where X = the number of workers who have a high school diploma. The number of adult workers that you expect to have a high school diploma and not pursue any further education is the mean, \mu = np = (20)(0.41) = 8.2 .

Example 7

The lifetime risk of developing pancreatic cancer is about one in 78, which is about 1.28%. Suppose we randomly sample 200 people. Let X = the number of people who will develop pancreatic cancer.

  1. What is the probability distribution for X?
  2. Calculate the mean and standard deviation of X.
  3. Find the probability that at most eight people develop pancreatic cancer.
  4. Is it more likely that five or six people will develop pancreatic cancer? Justify your answer numerically.

Answer:

  1. X ~ Bin(200, 0.0128)
  2. The mean = np = 200(0.0128) = 2.5  and  the standard deviation = \sqrt{npq} = \sqrt{(200)(0.0128)(0.9872)} \approx 1.5897.
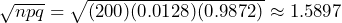  3. P(X ≤ 8) = 0.9988
  4. P(X = 5) = 0.0707  and P(X = 6) = 0.0298, so it is more likely that five people will develop cancer than six.

Example 8

During the 2013 regular NBA season, DeAndre Jordan of the Los Angeles Clippers had the highest field goal completion rate in the league. DeAndre scored with 61.3% of his shots. Suppose you choose a random sample of 80 shots made by DeAndre during the 2013 season. Let X = the number of shots that scored points.

  1. What is the probability distribution for X ?
  2. Calculate the mean and standard deviation of X.
  3. Find the probability that DeAndre scored with 60 of these shots.
  4. Find the probability that DeAndre scored with more than 50 of these shots.

Answer:

  1. X ~ Bin(80, 0.613)
  2. The mean = np = 80(0.613) = 49.04. We would expect DeAndre to score with about 49 of 80 shots. The standard deviation = \sqrt{npq} = \sqrt{(80)(0.613)(0.387)} \approx {4.3564}
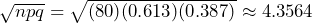
  3. P(X = 60) = 0.0036, so the probability of scoring with exactly 60 shots is low and will occur about 0.36% of the time.
  4. P(X > 50) = 1 – P(x ≤ 50) = 1 – 0.6282 = 0.3718, so the probability of scoring with more than 50 shots is about 37.18%.

Example 9: Binomial or Not

For each scenario, determine if the situation described qualifies as a binomial experiment.

  1. Sixty-five percent of people pass the state driver’s exam on the first try. A group of 50 individuals who have taken the driver’s exam is randomly selected. Whether the individual passed or failed is noted.
  2. A lacrosse team is selecting a captain. The names of all the seniors are put into a hat, and the first three that are drawn will be the captains. The names are not replaced once they are drawn (one person cannot be two captains). You want to see if the captains all play the same position.
  3. A company manufactures thousands of components each day, 8% of which are defective. Over the course of a few weeks, a random sample of 100 components is taken and it is noted whether each component is defective or not defective.

Answers:

  1. This is a binomial problem because there is only a success or a failure, and there are a finite number of trials taken from a large population. The probability of a success stays the same for each trial because we can assume independence for each trial.
  2. This is not binomial because the names are not replaced, which means the probability changes for each time a name is drawn. This violates the condition of independence.
  3. This is a binomial experiment. Because the number of components is large compared to the sample size, the assumption of independent trials is met. There is a general 8% defect rate, so the probability of a success will remain constant and there are a fixed number of trials.

Videos

YouTube Video the Binomial Distribution and Binomial Probability Function

Sources

“NBA Statistics – 2013,” ESPN NBA, 2013. Available online at http://espn.go.com/nba/statistics/_/seasontype/2 (accessed May 15, 2013).

“What are the key statistics about pancreatic cancer?” American Cancer Society, 2013. Available online at http://www.cancer.org/cancer/pancreaticcancer/detailedguide/pancreatic-cancer-key-statistics (accessed May 15, 2013).

License

Icon for the Creative Commons Attribution 4.0 International License

Introduction to Statistics for Engineers Copyright © by Vikki Maurer & Jeff Crabill & Linn-Benton Community College is licensed under a Creative Commons Attribution 4.0 International License, except where otherwise noted.

Feedback/Errata

Comments are closed.