8.3 Confidence Interval for a Population Proportion
During an election year, Americans are inundated with polls and articles in the newspaper that state confidence intervals in terms of proportions or percentages. For example, a Reuters.com poll on July 16, 2024 stated candidate Trump had a slight lead over President Biden, 43% to 41%, with a 3% margin of error. Often, election polls are calculated with 95% confidence, so the pollsters would be 95% confident that the true proportion of voters who favored candidate Trump was between 40% and 46% while the true proportion of voters who favored President Biden was between 38% and 44%.
Investors in the stock market are interested in the true proportion of stocks that go up and down each week. Businesses that sell laptop computers are interested in the proportion of households in the United States that own laptop computers. Engineers are interested in the true proportion of defective items from a production run. Confidence intervals can be calculated for the true proportion just as we constructed confidence intervals for the true population mean.
The procedure to find the confidence interval for a population proportion is similar to that of finding a confidence interval for the population mean, in that we need a point estimate, a critical value, and a standard error. The sampling distribution must be carefully considered before we begin.
Binomial Random Variable
When we observe an outcome that meets or does not meet a standard or is a success or a failure, then we have a binomial random variable. If X is a binomial random variable, then ![]() , where
, where ![]() is the number of trials and
is the number of trials and ![]() is the probability of a success. If we consider the proportion of outcomes that meet or do not meet a standard, then the statistic
is the probability of a success. If we consider the proportion of outcomes that meet or do not meet a standard, then the statistic ![]() is the point estimator of the true population proportion of successes,
is the point estimator of the true population proportion of successes, ![]() . Recall also that
. Recall also that ![]() .
.
When we create the sample proportion, ![]() , we have added up the number of successes and divided it by the total number in the sample. If, for example, each failure is designated with a value of 0 and each success is designated with the value of 1, then
, we have added up the number of successes and divided it by the total number in the sample. If, for example, each failure is designated with a value of 0 and each success is designated with the value of 1, then ![]() is the sum of the successes and
is the sum of the successes and ![]() is the sample mean of the
is the sample mean of the ![]() values.
values.
With a large enough sample size, we know the Central Limit Theorem specifies the distribution of ![]() . When
. When ![]() is large and
is large and ![]() is not close to zero or one, we can use the normal distribution to approximate the binomial.
is not close to zero or one, we can use the normal distribution to approximate the binomial.
![]()
We can present the confidence interval for the population proportion, just a we did for the population mean.
Confidence Interval for Population Proportion
Point Estimate ![]() (Critical Value)(Standard Error)
(Critical Value)(Standard Error)
![]()
However, do you notice the problem with this confidence interval? It requires knowledge of the population proportion, which is exactly the thing we are trying to create a confidence interval for. The value of ![]() cannot be computed. You might wonder if we can simply use the sample proportion,
cannot be computed. You might wonder if we can simply use the sample proportion, ![]() in place of
in place of ![]() and calculate the confidence interval using the sample proportion? This is in fact how this confidence interval was constructed traditionally.
and calculate the confidence interval using the sample proportion? This is in fact how this confidence interval was constructed traditionally.
Confidence Interval for Population Proportion – Wald Method (Traditional Method)
Let be the number of successes in
independent Bernoulli trials, with success probability,
.
The 100(1 – )% Confidence Interval for
is given as
![]()
Use the Wald Method only when ![]() and
and ![]() are both greater than 10. It should never be used with small samples.
are both greater than 10. It should never be used with small samples.
This traditional method is often referred to as the Wald interval. Statistics is a vibrant field of study and it has been determined through simulation and research that creating a confidence interval for the true population proportion using this traditional method is somewhat poor. What this means is that if we were to use this plan to create many, many 95% confidence intervals, fewer than 95% of them would contain the population proportion. This is not what we want in a confidence interval! One issue that causes a problem is that often the value of ![]() is too near the values of 0 or 1 and/or the sample size is not very large. It is important to note that this interval does still get used, so it should be noted that a good rule is to use it only when both
is too near the values of 0 or 1 and/or the sample size is not very large. It is important to note that this interval does still get used, so it should be noted that a good rule is to use it only when both ![]() and
and ![]() are greater than 10. It should never be used with small samples.
are greater than 10. It should never be used with small samples.
There are many other confidence intervals for the population proportion, and one in particular, the Agresti-Coull confidence interval, proposed in 1998, has been shown to offer much more consistent coverage with a very simple fix. There are also several exact Binomial confidence intervals, so if you are using a statistical program, find out what method the program uses.
Agresti-Coull Confidence Interval for the Population Proportion, 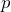
There is a certain amount of error introduced into the process of calculating a traditional confidence interval for a proportion. Because we do not know the true proportion for the population, we are forced to use point estimates to calculate the appropriate standard deviation of the sampling distribution. Studies have shown that the resulting estimation of the standard deviation can be flawed.
Fortunately, there is a simple adjustment that allows us to produce more accurate confidence intervals. We simply pretend that we have four additional observations. Two of these observations are successes and two are failures. The new sample size, then, is ![]() + 4, and the new count of successes is
+ 4, and the new count of successes is ![]() + 2.
+ 2.
Confidence Interval for Population Proportion – Agresti-Coull Method (Modern Method)
Let ![]() be the number of successes in
be the number of successes in ![]() independent Bernoulli trials, with success probability,
independent Bernoulli trials, with success probability, ![]() .
.
Then ![]() . Let
. Let ![]() =
= ![]() + 4 and let
+ 4 and let ![]() .
.
The 100(1 – ![]() )% Confidence Interval for
)% Confidence Interval for ![]() is given as
is given as
![]()
Because this confidence interval is for the population proportion, ![]() , if the lower limit is negative, then replace it with zero. Similarly, if the upper confidence limit is greater than one, then replace it with one.
, if the lower limit is negative, then replace it with zero. Similarly, if the upper confidence limit is greater than one, then replace it with one.
Example 1 – Comparing Confidence Intervals Small Sample
A random sample of 25 off-road tires were examined to determine if they contained a serious flaw. There were 6 tires in the sample with this flaw. Create a 95% confidence interval using the traditional method and with the Agresti-Coull method for the true proportion of tires with a serious flaw. Compare the confidence intervals.
Solutions:
Both confidence intervals will be 95% intervals, so ![]() = 1.96.
= 1.96.
- For
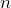 = 25 and
= 25 and 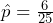 = 0.24, the traditional confidence interval is calculated as
= 0.24, the traditional confidence interval is calculated as
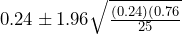 so the 95% confidence interval is (0.073, 0.407). Using the traditional method, we are 95% confident that the proportion of tires with a serious flaw is between 7.3% and 40.7%.
so the 95% confidence interval is (0.073, 0.407). Using the traditional method, we are 95% confident that the proportion of tires with a serious flaw is between 7.3% and 40.7%. - Six tires out of 25 contained a serious flaw, so
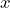 = 6 and
= 6 and 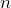 = 25. For the Agresti-Coull method, we will use
= 25. For the Agresti-Coull method, we will use 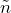 = 25 + 4 = 29 and
= 25 + 4 = 29 and 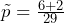 . The confidence interval is calculated as
. The confidence interval is calculated as
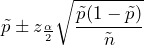
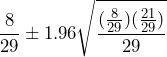
The confidence interval is (0.113, 0.439). Using the Agresti-Coull method, we are 95% confident that the true proportion of tires with a serious flaw is between 11.3% and 43.9%.
The margin of error for the traditional method was 0.1674 and for the Agresti-Coull method was 0.1627. The major difference in this case is the shift of the point estimate. Note with the traditional method, it was used despite ![]() = 6 and
= 6 and ![]() = 19.
= 19.
Example 2 – Large Sample Opinion Poll
In the same Reuters.com poll from the section opener, it was reported that in a sample of 1202 U.S. adults nationwide, 80% or 962 adults out of 1202, agreed with the statement, “The country is spiraling out of control.” Create a 95% confidence interval for the population proportion of all U.S. adults who agree with the statement using the traditional method and with the Agresti-Coull method. Compare the confidence intervals.
Solutions:
Both confidence intervals will be 95% intervals, so ![]() = 1.96.
= 1.96.
- For
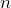 = 1202 and
= 1202 and 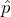 = 0.80, the traditional confidence interval is calculated as follows:
= 0.80, the traditional confidence interval is calculated as follows:
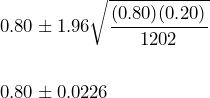
The 95% traditional confidence interval is (0.777, 0.823). Using the traditional method, we are 95% confident that the proportion of U.S. adults who agree with the statement is between 77.7% and 82.3%.
- For the Agresti-Coull method, we will use
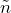 = 1202 + 4 = 1206 and
= 1202 + 4 = 1206 and 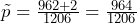 . The confidence interval is calculated as follows:
. The confidence interval is calculated as follows:
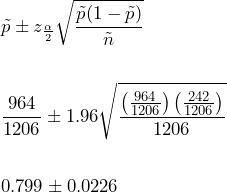
The Agresti-Coull confidence interval is (0.776, 0.822). Using the Agresti-Coull method, we are 95% confident that the proportion of U.S. adults who agree with the statement is between 77.6% and 82.2%.
The margin of error for both methods was 0.0226 and the subsequent confidence intervals were nearly identical. For large sample sizes, both approaches will provide similar results.
Because of the divisor involving the sample size, larger samples will always yield narrower and more precise confidence intervals than smaller samples. The Agresti-Coull method has a greater impact on the smaller sample. It shifts the point estimate closer to 0.5. It has a smaller impact on the margin of error.
Calculating the Sample Size
If researchers desire a specific margin of error (ME), then they can use the error bound formula to calculate the required sample size.
The margin of error formula for a population proportion ![]()
Solving for the sample size, n, gives you an equation for the sample size.
![]()
Example 3 – Determine Sample Size to Achieve a Specified Margin of Error
Suppose a mobile phone company wants to determine the current percentage of customers aged 50+ who use text messaging on their cell phones. How many customers aged 50+ should the company survey in order to be 90% confident that the estimated (sample) proportion is within three percentage points of the true population proportion of customers aged 50+ who use text messaging on their cell phones.
Solution:
From the problem, we know that Margin of Error = 0.03 (3%=0.03), and because the confidence level is 90%, we know ![]() = 0.10 and
= 0.10 and ![]() =
= ![]() = 1.645.
= 1.645.
In order to find ![]() , we need to know the estimated (sample) proportion
, we need to know the estimated (sample) proportion ![]() . Remember that
. Remember that ![]() . However, we do not know
. However, we do not know ![]() yet since the sample has not yet been taken. Since we multiply
yet since the sample has not yet been taken. Since we multiply ![]() and
and ![]() together, we make them both equal to 0.5 because
together, we make them both equal to 0.5 because ![]() = (0.5)(0.5) = 0.25 results in the largest possible product. The largest possible product gives us the largest
= (0.5)(0.5) = 0.25 results in the largest possible product. The largest possible product gives us the largest ![]() . This gives us a large enough sample so that we can be 90% confident that we are within three percentage points of the true population proportion. To calculate the sample size
. This gives us a large enough sample so that we can be 90% confident that we are within three percentage points of the true population proportion. To calculate the sample size ![]() , use the formula and make the substitutions.
, use the formula and make the substitutions.
![]()
Round the sample size to the next higher value. The sample size should be 752 cell phone customers aged 50+ in order to be 90% confident that the estimated (sample) proportion is within three percentage points of the true population proportion of all customers aged 50+ who use text messaging on their cell phones.
Videos
YouTube Confidence Interval for a Population Proportion
Sources
Exclusive: Four in five Americans fear country is sliding into chaos. (2024, July 16). Reuters.com. Retrieved July 16, 2024, from https://www.reuters.com/world/us/four-five-americans-fear-country-is-sliding-into-chaos-reutersipsos-poll-finds-2024-07-16/
Mmst, D. R. M. (2021, December 15). Five confidence intervals for proportions that you should know about. Medium. https://towardsdatascience.com/five-confidence-intervals-for-proportions-that-you-should-know-about-7ff5484c024f


Feedback/Errata