4.3 Conditional Probability
We know probability is a measure of uncertainty but the amount of uncertainty can potentially change as new information becomes available. This is the core idea behind a probability concept called conditional probability. Suppose each person at a gathering is given a ticket, some blue and some yellow. A single ticket will be randomly selected to win a prize. Initially, each person’s probability of winning depends on the total number of blue and yellow tickets given out. However, suppose a ticket is randomly selected, and before revealing the name on the ticket, it is announced that the ticket is yellow! This changes the information available and it changes the probability of winning. Finding the probability of an event given that some other event has happened changes the sample space used to calculate the probability.
Conditional Probability
Because additional information can change the probability of an event, having a visual representation of the entire sample space will be helpful. As we noted in the previous section, a contingency table provides a way of organizing and presenting data related to two different variables. We can analyze a contingency table to calculate conditional probabilities. Having information about the occurrence of an event will restrict our attention to a certain portion of the sample space and to a certain row or column of the contingency table. Let’s explore the idea of using a contingency table as we calculate conditional probabilities and take note of where the parts of the calculation come from. This will help us create a formula for conditional probability.
Example 1: Exploring Conditional Probability with a Contingency Table
One hundred randomly selected hikers were asked about the areas in which they prefer to hike. Whether the hiker was female or male was also noted. The data is presented in a contingency table. Notice the table is missing some values.
| Sex | The Coastline | Near Lakes and Streams | On Mountain Peaks | Total |
|---|---|---|---|---|
| Female | 18 | 16 | ___ | 45 |
| Male | ___ | ___ | 14 | 55 |
| Total | ___ | 41 | ___ | ___ |
Define several events: M = being male, F = being female, C = prefers the coastline, L = prefers lakes and streams, and P = prefers mountain peaks.
Complete the table and find each of the following:
- Find the probability the person is female. Make a note the denominator of the calculation and its meaning.
- Find the probability the person prefers hiking on the coastline. Make a note of the denominator of this calculation and its meaning.
- Find the probability that a person is female given that the person prefers hiking near lakes and streams. Make a note the sample space for this calculation and the parts of the contingency table used in the calculation.
- Find the probability that a person prefers mountain peeks given that the person is male. Make a note the sample space for this calculation and the parts of the contingency table used in the calculation.
Answers:
Use the row and column totals to fill in the missing data values.
| Sex | The Coastline | Near Lakes and Streams | On Mountain Peaks | Total |
|---|---|---|---|---|
| Female | 18 | 16 | 11 | 45 |
| Male | 16 | 25 | 14 | 55 |
| Total | 34 | 41 | 25 | 100 |
- P(F) =
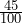 . Notice the total number in the sample space is 100. The probability is calculated using the entire sample of 100 individuals.
. Notice the total number in the sample space is 100. The probability is calculated using the entire sample of 100 individuals. - P(C) =
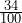 . Notice the total number in the sample space is 100. The probability is calculated using the entire sample of 100 individuals.
. Notice the total number in the sample space is 100. The probability is calculated using the entire sample of 100 individuals. - The word given tells you that this is a conditional probability. We already know the person prefers lakes and streams, so we focus on the reduced sample space of just those 41 individuals. From those 41 individuals who prefer lakes and streams, 16 of them are female. We focus on the 16 individuals who are female AND prefer lakes and streams, so focus on the number of individuals in the event
 . The probability calculation becomes P(F given L) =
. The probability calculation becomes P(F given L) = 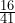 .
. - The word given tells you that this is a conditional probability. We already know the person is male, so we focus on the reduced sample space of just those 55 males. From those 55 individuals who are male, 14 of them prefer mountain peaks. We focus on the 14 individuals who are male AND prefer mountain peaks, so focus on the number of individuals in the event
 . The probability calculation becomes P(P given M) =
. The probability calculation becomes P(P given M) = 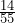 .
.
As we noticed in Example 1, when we know an event has already occurred, we can focus on part of the sample space. This leads us to new formulas for calculating conditional probabilities.
Conditional Probability Formula
The conditional probability of A given B is written P(A|B) and is the probability that event A will occur given that the event B has already occurred.
P(A |B ) = ![]() where P(B ) is greater than zero.
where P(B ) is greater than zero.
Example 2: Conditional Probabilities Using Formulas
The tendency to use one’s left hand or right hand in various daily tasks, such as when writing, is a widely studied human characteristic. For children learning to write, rates of left-handedness, right-handedness, or both-handedness were compared for blind and sighted children, with data summarized in the table.
| Vision | Left-Handed | Right-Handed | Both-Handed | Total |
| Blind | 424 | 896 | 67 | 1387 |
| Sighted | 101 | 714 | 16 | 831 |
| Total | 525 | 1610 | 83 | 2218 |
Let’s denote the events B = the child is blind, S = the child is sighted, R = the child is right-handed, L = the child is left-handed.
For a randomly selected child, compute the following probabilities:
- P( B )
- P( S )
- P( R )
- P( L )
- P( R and B ) and P( L and B )
- P( S and L ) and P( S and R )
- P( B |R )
- P( R |B )
- P( L |B )
- P( B |L )
Answers:
- P( B ) =
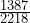 ≈ 0.63
≈ 0.63 - P( S ) =
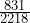 ≈ 0.37
≈ 0.37 - P( R ) =
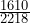 ≈ 0.73
≈ 0.73 - P( L ) =
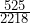 ≈ 0.24
≈ 0.24 - P(R
 B ) =
B ) = 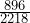 ≈ 0.40; P(L
≈ 0.40; P(L  B ) =
B ) = 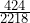 ≈ 0.20
≈ 0.20 - P(S
 L ) =
L ) = 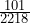 ≈ 0.05; P(S
≈ 0.05; P(S  R ) =
R ) = 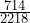 ≈ 0.32
≈ 0.32 - P( S |L ) =
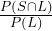 =
= 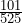 ≈ 0.20
≈ 0.20 - P( R |B ) =
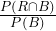 =
= 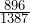 ≈ 0.65
≈ 0.65 - P( L |B ) =
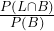 =
= 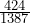 ≈ 0.31
≈ 0.31 - P( B |L ) =
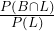 =
= 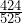 ≈ 0.81
≈ 0.81
Notice for this group of children, if it is known that the child is blind, the probability they are also right handed is double the probability they are also left handed. If it is known the child is left-handed, the probability they are also blind is four times the probability they are also left handed. These sorts of relationships suggest the need for future studies.
Sometimes we know the conditional probability involving two events, and we would like to reason out the probability the events occur at the same time. We can use our conditional probability formula to create a new relationship.
Multiplication Rule
P(A |B ) = ![]() Multiplying both sides of the equation by P(B ) gives, P(A
Multiplying both sides of the equation by P(B ) gives, P(A ![]() B) = P(A |B )P(B).
B) = P(A |B )P(B).
Example 3: Using the Multiplication Rule and Risk Assessment
After the space shuttle Challenger’s 1986 explosion, it was concluded that O-rings do not seal properly at low temperatures and combustion gas leaked through a joint (called a blowby) in one of the booster rockets causing the catastrophe. In a later analysis, data from 23 preaccident launches was used to predict O-ring performance. The findings were published in the Journal of the American Statistical Association, December 1989 issue, in an article titled, “Risk Analysis of the Space Shuttle: Pre-Challenger Prediction of Failure” by Dilal, Fowlkes, and Hoadley. The analysis concluded the predicted probability of erosion of an O-ring, at 31 °F and 200 psi, which are the conditions at which the Challenger was launched, is 0.95. The study further concluded that the occurrence of a blowby given erosion is 0.286. Find the probability of erosion and blowby.
Answer: We know from the article that P(O-ring erosion) = 0.95 and P(O-ring blowby | O-ring erosion) = 0.286
We can find P(O-ring erosion AND O-ring blowby) using the multiplication rule.
P(O-ring erosion ![]() O-ring blowby) = (0.286)(0.95) ≈ 0.27.
O-ring blowby) = (0.286)(0.95) ≈ 0.27.
Example 4: Using Conditional Probabilities
Rapid antigen tests used to diagnosis COVID-19 are not 100% accurate. With any test, there are always cases when the test is positive but the person does not have the infection (false positive) and cases where the test is negative but the person does have the infection (false negative). The rapid antigen test is most accurate when the person taking the test has symptoms of COVID-19 and the test is taken within seven days of symptom onset. According to a July 2022 entitled “Rapid, point-of-care antigen tests for diagnosis of SARS-CoV-2 infection,” if 5% of the population actually had COVID-19, data shows 4.5% would test positive. 11% of those who test positive would have a false positive result. Of those who test negative, 1% would actually have COVID-19, so would have a false negative.
- Interpret this false positive and false negative information using conditional probability.
- Use the multiplication rule to predict how many people out of 100,000 would have COVID-19 and test positive.
- Use the multiplication rule to predict how many people out of 100,000 would have COVID-19 and test negative.
- Create a contingency table using this information based on 100,000 people who have symptoms of COVID-19 and take a rapid antigen test.
Answers:
- The probability of the person does not have COVID-19 given that they tested positive for COVID-19 is 0.11. The probability of the person having COVID-19 given that they tested negative for COVID-19 is 0.01.
- P(Does Not Have COVID-19 | Test Positive) = 0.11, so P(Have COVID-19 | Test Positive) = 0.89. We were given P(Test Positive) = 0.045. P(Have COVID-19 and Test Positive) = (0.89)(0.045) = 0.04005. Out of 100,000 people taking the test, (0.04005)(100,000) = 4005 people would test positive and have COVID-19.
- P(Does Have COVID-19 | Test Negative) = 0.01. We were given P(Test Positive) = 0.045, so P(Test Negative) = 1 – 0.045 = 0.995. P(Have COVID-19 and Test Negative) = (0.01)(0.995) = 0.00995. Out of 100,000 people taking the test, (0.00995)(100,000) = 995 people would test negative and have COVID-19.
- Contingency table based on 100,000 people who are symptomatic for COVID-19:
| Test Positive for COVID-19 | Test Negative for COVID-19 | Total | |
| Have COVID-19 | 4005 | 995 | 5000 |
| Does Not Have COVID-19 | 495 | 94,505 | 95,000 |
| Total | 4500 | 95,500 | 100,000 |
Sources
“Left-handedness in blind and sighted children.” Caliskan E, Dane S. Laterality. 2009 Mar;14(2):205-13. doi: 10.1080/13576500802586251. Epub 2009 Jan 14. PMID: 19142794. Available online at https://pubmed.ncbi.nlm.nih.gov/19142794/.
“Risk Analysis of the Space Shuttle: Pre-Challenger Prediction of Failure”, Author(s): Siddhartha R. Dalal, Edward B. Fowlkes, Bruce Hoadley, Source: Journal of the American Statistical Association, Vol. 84, No. 408 (Dec., 1989), pp. 945-957 Published by: American Statistical Association
Dinnes J, Sharma P, Berhane S, van Wyk SS, Nyaaba N, Domen J, Taylor M, Cunningham J, Davenport C, Dittrich S, Emperador D, Hooft L, Leeflang MMG, McInnes MDF, Spijker R, Verbakel JY, Takwoingi Y, Taylor-Phillips S, Van den Bruel A, Deeks JJ. Rapid, point‐of‐care antigen tests for diagnosis of SARS‐CoV‐2 infection. Cochrane Database of Systematic Reviews 2022, Issue 7. Art. No.: CD013705. DOI: 10.1002/14651858.CD013705.pub3. Accessed 18 March 2024.
The likelihood an event will occur, if another event has already occurred.
A display of data in rows and columns for two different variables.


Feedback/Errata