4.4 Independent Events
Get out a coin and start flipping it, making sure it rotates several times before landing. The theoretical probability the coin lands heads up (H) is 0.5. Suppose you observe five heads in a row: H, H, H, H, H. What is the probability the coin lands with tails up (T) on the next flip? Would it surprise you to know that many people think that the chances of the coin landing tails up on the next flip is higher than 0.5 because there have already been so many heads in a row? Humans tend to want to project their own subjective ideas to random events, such as coin flips. The reality of this situation is that the coin has no memory. It is not keeping track of its own pattern of heads or tails. Each flip of the coin occurs as if it is the first flip, so the probability of landing heads up is 0.5 and the probability of it landing tails up is 0.5 every time it is flipped. This is the core idea behind the idea that events are independent.
Independent Events
Two events A and B are independent if the knowledge that one occurred does not affect the chance the other occurs. If two events are NOT independent, then we say that they are dependent. The following three formulas apply to independent events.
Independent Events
For independent events A and B, each of the following will be true:
- The probability of event A, given that event B has occurred, is the same as the probability of A. [latex]P(A|B) = \frac{P(A \cap B)}{P(B)} = P(A).[/latex]
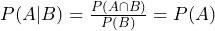- The probability of event B, given that event A has occurred, is the same as the probability of B. [latex]P(B|A) = \frac{P(B \cap A)}{P(A)} = P(B).[/latex]
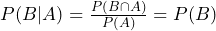- The probability of events A and B happening at the same time is the same as P(A) multiplied by P(B). In other words, [latex]P(A \cap B) = P(A)P(B).[/latex]
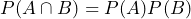Any of the three relationships can be used to demonstrate events are independent.
Why is the idea of independence important for a future engineer or scientist?
In engineering, it’s crucial to assess the probability of different events occurring, such as component failures, system malfunctions, or environmental hazards. Knowing whether events are independent allows engineers to accurately calculate the overall probability of multiple events happening simultaneously. For example, in structural engineering, understanding the independence of failure events for different components is essential for assessing the reliability of a structure under various loading conditions.
In the biological, physical, and chemical sciences and in fields like materials science, environmental engineering, and manufacturing, engineers and scientists rely on statistical analysis and experimental design to gather and interpret data. Knowing when events are independent allows engineers and scientists to apply appropriate statistical methods, such as hypothesis testing, regression analysis, or design of experiments, ensuring accurate conclusions and reliable predictions.
Example 1: Components and Independent Events
A redundant system is designed for an aircraft. The system consists of two identical components, A and B, manufactured at different times and not connected to each other in any way, so the event that the component A functions and the event that the component B functions are independent events. The system will operate successfully if at least one of the components functions. Because these components are identical, they will have the same probability of functioning. Suppose the probability of each component functioning is 0.75, that is, P(A functions) = P(B functions) = 0.75.
- Find the probability both components function.
- Find the probability component A functions given that component B functions.
- Find the probability component B functions given that component A functions
Answers:
- Knowing two events are independent allow us to find the probability of both events happening at the same time by multiplying their individual probabilities. P(A functions AND B functions) = P( A functions [latex]\cap[/latex] B functions) = P(A functions)P(B functions) = (0.75)(0.75) = 0.5625.
- P(A function given B functions) = P(A functions | B functions) = P(A functions) = 0.75. Because the events are independent, knowledge of component B functioning does not change the probability of component A functioning.
- P(B function given A functions) = P(B functions | A functions) = P(B functions) = 0.75. Because the events are independent, knowledge of component A functioning does not change the probability of component B functioning.
Sampling and Independent Events
When we sample from a population, we aim for our sample to be representative of the population as a whole. If events are independent, each member of the population has an equal chance of being included in the sample, regardless of whether other members have been included. This ensures that our sample accurately reflects the characteristics of the population. Many statistical tests we will study in this class rely on the assumption of independence between sampled observations.
Sampling from a population may be done with replacement or without replacement.
- With replacement: If each member of a population is replaced after it is picked, then that member has the possibility of being chosen more than once. When sampling is done with replacement, then events are considered to be independent, meaning the result of the first pick will not change the probabilities for the second pick.
- Without replacement: When sampling is done without replacement, each member of a population may be chosen only once. In this case, the probabilities for the second pick are affected by the result of the first pick. The events are considered to be dependent or not independent.
In sampling without replacement, the size of the sample relative to the size of the population affects the assumption of independence. Generally, when the sample size is small relative to the population size, the assumption of independence may hold true. There isn’t a specific threshold for how small the sample must be compared to the population to assume independence. However, as a rule of thumb, if the sample size for a simple random sample is no more than 5% of the population size, the assumption of independence is often considered reasonable. This guideline is based on the concept that as the sample size increases relative to the population size, the probability of selecting an individual observation changes with each selection. Therefore, when the sample size is a small proportion of the population size, the impact of this change in probabilities is minimized, and the assumption of independence is more likely to hold.
Example 2: Sampling With or Without Replacement and Independence
Scenario 1: A production run consists of 4 components, A, B, C, and D.
Question: If we sample two components from this production run, without replacement, what is the probability of getting component A followed by component B? Are these events independent?
Answer: In the first draw, the probability of getting component A is [latex]\frac{1}{4}[/latex]. Because we are not putting component A back, there are only three components for the second draw, so the probability of getting component B in the second draw is [latex]\frac{1}{3}[/latex]. Each component does not have the same probability of being selected, thus emphasizing the fact that these events are not independent.
Scenario 2: A population consists of 5000 people, including you and your best friend.
Question: If we take a sample of two people from this population, without replacement, what is the probability of selecting you and then your best friend? Are these events independent?
Answer: In the first draw, the probability of selecting you is [latex]\frac{1}{5000}[/latex] = 0.0002. Because you are not getting put back into the population, in the second draw, the probability of selecting your best friend is [latex]\frac{1}{4999} \approx 0.00020004[/latex]. Notice that with a large population and a small sample size, the probability of each selection barely changes, so the assumption of independent events is reasonable.
