5.3 Expected Value and Standard Deviation of a Discrete Distribution

Jeff Crabill; Vikki Maurer

5.3 Expected Value and Standard Deviation of a Discrete Distribution

Expected Value

The expected value is often referred to as the long-term average or mean. This means that over the long period of doing an experiment over and over, you would expect this average.

Suppose you will toss a coin and record the result. What is the probability that the result will be heads? We tend to have a sense of this theoretical probability and know the probability is 0.5 that the coin will land heads up. If you flip a coin two times, does your understanding of theoretical probability tell you that these flips will result in one heads and one tail? You might toss a fair coin ten times and record nine heads. Does this seem to violate the expectation? We must keep in mind that probability does not describe the short-term results of an experiment. It gives information about what can be expected in the long term. To demonstrate this, Karl Pearson once tossed a fair coin 24,000 times! He recorded the results of each toss, obtaining heads 12,012 times. In his experiment, Pearson illustrated the Law of Large Numbers.

The Law of Large Numbers states that, as the number of trials in a probability experiment increases, the difference between the theoretical probability of an event and the relative frequency approaches zero. In other words, the theoretical probability and the relative frequency get closer and closer together as more trials are carried out. When evaluating the long-term results of statistical experiments, we often want to know the average outcome. This long-term average is known as the mean or expected value of the experiment and is denoted by the Greek letter μ. In other words, after conducting many trials of an experiment, you would expect this average value.

The Mean of a Discrete Distribution

Just like a set of data, a discrete probability distribution also has a center that we can measure. You might think, “What’s the average dice roll for a six-sided die?” If we look at that probability distribution, you’ll see that the average or center can be found at 3.5, because each outcome has the same probability.

Example 1 – Probability Distribution for a Roll of a Die

Let’s consider the experiment of rolling one fair six-sided die. If we plan to observe the number of dots, or pips, showing on the top face when the die is rolled, then the random variable X represents the number of pips showing. Because the random variable can take on the values 1, 2, 3, 4, 5, and 6, each with equal probability, we can create the probability distribution for the roll of a six-sided die:

Outcome

Probability

x = 1

1/6

x = 2

1/6

x = 3

1/6

x = 4

1/6

x = 5

1/6

x = 6

1/6

What’s the “average” outcome? Where is the “center” of the probability distribution? In this case, we can use the same approach that we used when dealing with data and find an average of the outcomes of the six possible outcomes: 1, 2, 3, 4, 5, and 6. We can add up the values of the random variable and divide by 6 to get a mean of 3.5. We can do that because they all have the same probability. But what if one had a higher probability? How would affect the mean?

Let’s explore the question raised in the previous example and look at an example with data. Consider three data values, 1, 2, and 3, each occurring with a different frequency. You may suspect that the average data value will be affected by the frequency, and in the same way, a PDF will be similarly affected.

Suppose you have a frequency table as shown next:

Data Value	Frequency
1	2
2	5
3	15

Hopefully, it seems clear that the average value is NOT 2, because there are fifteen 3s that must be considered! With so many values of 3, the mean will be well above 2. Notice that there are 2 + 5 + 15 = 22 total data values, once we take into account the frequency. The mean would be computed as follows:

$\bar{x}=\displaystyle\frac{1(2)+2(5)+3(15)}{22}$

and $\bar{x}=2.6$ .

The same is true for the center of a discrete probability distribution. We have to consider a weighted average so that we take the probability of each outcome into account.

Expected Value of a Discrete Distribution

The expected value of a discrete random variable can be defined as follows:

$E(X) = \displaystyle\sum_{i=1}^n x P(x) dx$

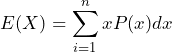
where P(x) is the probability density function. Note the expected value is also called the mean, $\mu$ .

Example 2 – Expected Value Table

A soccer team plays soccer zero, one, or two days a week. The probability that they play zero days is 0.2, the probability that they play one day is 0.5, and the probability that they play two days is 0.3. Find the long-term average or expected value, μ, of the number of days per week the team plays soccer.

Let random variable X = the number of days the soccer team plays soccer per week. X takes on the values 0, 1, 2. Construct a PDF table, adding a column x ⋅ P(x). In this column, you will multiply each x value by its probability.

Expected Value Table. This table is called an expected value table. The table helps you calculate the expected value or long-term average.

x	P(x)	x ⋅ P(x)
0	0.2	(0)(0.2) = 0
1	0.5	(1)(0.5) = 0.5
2	0.3	(2)(0.3) = 0.6

Add the last column x ⋅ P(x) to find the long term average or expected value: (0)(0.2) + (1)(0.5) + (2)(0.3) = 0 + 0.5 + 0.6 = 1.1. The expected value is 1.1. The soccer team would, on the average, expect to play soccer 1.1 days per week. The number 1.1 is the long-term average or expected value if the soccer team plays soccer week after week after week. We say μ = 1.1.

Example 3 – Expected Profit Five Number Draw

Suppose you play a game of chance in which five numbers are chosen from 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. A computer randomly selects five numbers from zero to nine, with replacement. You will pay $2 to play and could profit $100,000, if you match all five numbers in order (you get your $2 back plus $100,000). Over the long term, what is your expected profit of playing the game?

Set up an expected value table for the amount of money you can profit.

Let the random variable X = the amount of money you profit. The values of x are not 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Since you are interested in your profit (or loss), the values of x are 100,000 dollars and −2 dollars.

To win, you must get all five numbers correct, in order. The probability of choosing one correct number is
$\displaystyle\frac{{1}}{{10}}$ because there are ten numbers. Because the numbers are drawn with replacement a number may occur more than once. Each selection is independent. The probability of choosing all five numbers correctly and in order is $\displaystyle(\frac{{1}}{{10}})^{5}$ = 0.00001.

The expected value table is as follows:

	x	P(x)	x P(x)
Loss	–$2	0.99999	(–2)(0.99999)
Profit	$100,000	0.00001	(100000)(0.00001)

Αdd the last column to find the expected value: –1.99998 + 1 = –0.99998

Since –0.99998 is close to –1, you would, on average, expect to lose approximately $1 for each game you play. However, each time you play, you either lose $2 or profit $100,000. The $1 is the average or expected LOSS per game after playing this game over and over.

Example 4 – Expected Profit Deck of Cards

You are playing a game of chance in which four cards are drawn from a standard deck of 52 cards. You guess the suit of each card before it is drawn. The cards are replaced in the deck on each draw. You pay $1 to play. If you guess the right suit every time, you get your money back and $256. What is your expected profit of playing the game over the long term?

To win, you must guess all four suits correctly. There are four suits in a standard deck of cards, so the probability of choosing the correct suit of one card is
$\displaystyle\frac{{1}}{{4}}$ . Because the cards are returned to the deck each time, each selection is independent. The probability of choosing all four suits correctly is $\displaystyle(\frac{{1}}{{4}})^{4}$ = 0.0039.

Let X = the amount of money you profit. The x-values are –$1 and $256 and the probabilities are given in the table:

	Outcome	P(X)
Win	$256	0.0039
Loss	-$1	0.9961

The expected value of this distribution is (0.0039)256 + (0.9961)(–1) = 0.9984 + (–0.9961) = 0.0023 or 0.23 cents. In other words, you expect to profit 0.23 cents each time you play.

The Standard Deviation of a Discrete Distribution

The expected value of a probability distribution provides a measure the center of the distribution of the random variable. We must also consider the spread of the distribution, in the same way we discussed the spread of a data set. Thus we can extend our definition of standard deviation on to a probability density function.

Standard Deviation of Discrete Probability Density Function

The standard deviation of a discrete probability density function is

$\sigma\left(X\right) = \sqrt{ \sum_{i=1}^n (x_i-\mu)^2 P(x) }$

where $\mu = E(X)$ and P(x) is the probability density function.

Like data, probability distributions have standard deviations. To calculate the standard deviation (σ) of a probability distribution, find each deviation from its expected value, square it, multiply it by its probability, add the products, and take the square root. To understand how to do the calculation, revisit the soccer team information from example 2. To find the standard deviation, add the entries in the column labeled (x – μ)²P(x) and take the square root.

x	P(x)	x ⋅ P(x)	(x – μ)²P(x)
0	0.2	(0)(0.2) = 0	(0 – 1.1)²(0.2) = 0.242
1	0.5	(1)(0.5) = 0.5	(1 – 1.1)²(0.5) = 0.005
2	0.3	(2)(0.3) = 0.6	(2 – 1.1)²(0.3) = 0.243

Add the last column in the table: 0.242 + 0.005 + 0.243 = 0.490. The standard deviation is the square root of 0.49, or σ = $\displaystyle\sqrt{0.49}$ = 0.7

Example 5 – Calculate the Standard Deviation

Find the expected value of the number of times a newborn baby’s crying wakes its parent after midnight. The expected value is the expected number of times per week a newborn baby’s crying wakes its parent after midnight. Calculate the standard deviation of the variable as well.

First, verify that $E(X)=2.1$ using columns one and two.

Next, compute the product of the squared deviation $(x-\mu)^2$ and the probability $P(x)$ for each outcome.

x

P(x)

(x – μ)² ⋅ P(x)

0

$P(x=0)=\frac{2}{50}$

$( 0 - 2.1 ) ^2 \cdot 0.04=0.1764$

1

$P(x=1)=\frac{11}{50}$

$(1-2.1)^2\cdot 0.22=0.2662$

2

$P(x=2)=\frac{23}{50}$

$(2-2.1)^2\cdot 0.46=0.0046$

3

$P(x=3)=\frac{9}{50}$

$(3-2.1)^2 \cdot0.18=0.1458$

4

$P(x=4)=\frac{4}{50}$

$(4-2.1)^2\cdot 0.08=0.2888$

5

$P(x=5)=\frac{1}{50}$

$(5-2.1)^2 \cdot0.02=0.1682$

Finally, add the values in the second column of the table to complete the computation.

0.1764 + 0.2662 + 0.0046 + 0.1458 + 0.2888 + 0.1682 = 1.05

The standard deviation of X is the square root of this sum: $\sigma\left(X\right) = \sqrt{1.05} \simeq 1.0247$

Example 5

On May 11, 2013 at 9:30 PM, the probability that moderate seismic activity (one moderate earthquake) would occur in the next 48 hours in a given region was about 21.42%. Suppose you make a bet that a moderate earthquake will occur in that region during this period. If you win the bet, you win $50. If you lose the bet, you pay $20. Let X = the amount of profit from a bet.

P(win) = P(one moderate earthquake will occur) = 21.42%

P(loss) = P(one moderate earthquake will not occur) = 100% – 21.42%

If you bet many times, will you come out ahead? Explain your answer in a complete sentence using numbers. What is the standard deviation of
X? Construct a table similar to the one in Example 5 to help you answer these questions.

Solution:

	x	P(x)	x(Px)	(x – μ)²P(x)
win	50	0.2142	10.71	[50 – (–5.006)]²(0.2142) = 648.0964
loss	–20	0.7858	–15.716	[–20 – (–5.006)]²(0.7858) = 176.6636

Mean = Expected Value = 10.71 + (–15.716) = –5.006.

If you make this bet many times under the same conditions, your long term outcome will be an average loss of $5.01 per bet.

$\displaystyle \text{Standard Deviation} = \sqrt{648.0964+176.6636} \simeq 28.7$

A probability distribution function is a pattern and a model for the behavior of a random variable. We try to match probability problem with a distribution in order to perform the necessary calculations. These distributions are tools to make solving probability problems easier. Each distribution has its own special characteristics. Learning the characteristics enables you to distinguish among the different distributions.

Mean and Standard Deviation of a Bernoulli Random Variable

We have previously described the Bernoulli trial, which is an experiment with a single trial and two outcomes. The PDF is given as

$P(X=x)=\begin{cases}1-p & x = 0\\p & x = 1\end{cases}$

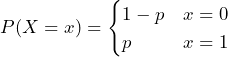
We can derive the expected value (mean) and standard deviation of a Bernoulli random variable.

The expected value is $E(x) = 1(p) + 0(1 - p) = p.$

The standard deviation is derived as follows:

$\sigma = \sqrt{(1 - p)^2(p) + (0 - p)^2(1 - p)}$

$= \sqrt{(1 - 2p + p^2)(p) + p^2(1 - p)}$

$= \sqrt{p - 2p^2 + p^3 + p^2 - p^3}$

$= \sqrt{p - p^2}$

$\sigma = \sqrt{p(1 - p)}$

Mean and Standard Deviation of a Bernoulli Random Variable

If $X \sim Bernoulli(p)$ , then $\mu_X = p$ and $\sigma_X = \sqrt{p(1 - p)}$ .

Example 6 – Bernoulli Random Variable

Roll one standard fair six-sided die with 1, 2, 3, 4, 5, or 6 pips on the sides. If we define the random variable as X = 1 if we roll a 3 and X = 0 if we roll a 1, 2, 4, 5, or 6, then create the PDF and find its expected value and standard deviation.

Solution:

Each side is equally likely, so the probability of observing a 3 in a single roll is $\frac{1}{6}$ , so $p = \frac{1}{6}.$

The PDF for this Bernoulli trial is 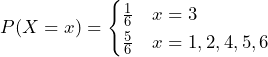$P(X = x) = \begin{cases}\frac{1}{6} & x = 3\\\frac{5}{6} & x = 1, 2, 4, 5, 6\end{cases}$

We can find the expected value, E(x) = p, so E(x) = $\frac{1}{6}$

The standard deviation is $\sigma =\sqrt{p(1 - p)} = \sqrt{\frac{1}{6} \frac{5}{6}} = \sqrt{\frac{5}{36}} \approx 0.37$

Sources

“World Earthquakes: Live Earthquake News and Highlights,” World Earthquakes, 2012. http://www.world-earthquakes.com/index.php?option=ethq_prediction (accessed May 15, 2013).

License

Icon for the Creative Commons Attribution 4.0 International License

Introduction to Statistics for Engineers Copyright © by Vikki Maurer & Jeff Crabill & Linn-Benton Community College is licensed under a Creative Commons Attribution 4.0 International License, except where otherwise noted.

Feedback/Errata

Comments are closed.