9.2 Hypotheses Testing Overview
Have you ever watched television shows such as Law and Order, where criminal trials are depicted? The logic of a criminal trial is quite similar to the core ideas behind hypothesis testing.
| Criminal Trial | Hypothesis Testing |
|---|---|
| A crime has been committed. | A research question is posed. |
| A suspect is arrested. | A parameter of interest is identified. |
| An accusation of guilt is posed. | The alternate hypothesis is stated. |
| An assumption of innocence is made. | The null hypothesis is stated. |
| Evidence is gathered and presented as testimony. | Sampling occurs and test statistic is examined. |
| A jury deliberates and makes a decision. | A decision rule is followed. |
| The jury declares the defendant guilty. | Reject the null hypothesis. |
| The jury declares the defendant not guilty. | Fail to reject the null hypothesis. |
| An innocent person was found guilty. | Type I Error was made. |
| A guilty person was found not guilty. | Type II Error was made. |
In a criminal jury trial, the jury has to weigh the evidence against the assumption that the person is actually innocent. They must decide if the there is enough evidence to declare the person is guilty, beyond a reasonable doubt. There is uncertainty in a jury trial, just as in hypothesis testing, and errors can be made. For hypothesis testing, evidence is considered in the form of probability related the sample taken and the null distribution. Unfortunately, there is always a chance the sample is not representative of the population and an error is made based on relying on sample information. This is the nature of statistics. It is built on a firm foundation of probability.
Hypothesis testing is a systematic way to put claims about a group or a population on trial. To perform a hypothesis test, a statistician will perform some variation of these steps:
- Define hypotheses based on a research question.
- Collect sample data and set the criteria for a decision.
- Calculate the test statistic.
- Make a decision.
- Write a conclusion.
Hypotheses Statements
The actual hypothesis test begins by considering two hypotheses statements. They are called the null hypothesis and the alternative hypothesis. These hypotheses contain opposing viewpoints.
The Null Hypothesis (![]() ): The null hypothesis is a statement which is the opposite of the alternative hypothesis. The null hypothesis is typically written after the creation of the alternate hypothesis and provides a probability distribution that would exist if there were no treatment effect. This is the starting point that that must be assumed in order to demonstrate evidence that an effect exists beyond a reasonable doubt. It is similar to a jury trial where the defendant is assumed innocent at the start.
): The null hypothesis is a statement which is the opposite of the alternative hypothesis. The null hypothesis is typically written after the creation of the alternate hypothesis and provides a probability distribution that would exist if there were no treatment effect. This is the starting point that that must be assumed in order to demonstrate evidence that an effect exists beyond a reasonable doubt. It is similar to a jury trial where the defendant is assumed innocent at the start.
The Alternate Hypothesis (![]() ): The alternate hypothesis is a claim about the population and is often the first statement created. It is the statement that indicates there is an effect and is contradictory to the null hypothesis.
): The alternate hypothesis is a claim about the population and is often the first statement created. It is the statement that indicates there is an effect and is contradictory to the null hypothesis.
Since the null and alternative hypotheses are contradictory, you must examine evidence to decide if you have enough evidence to reject the null hypothesis or fail to reject the null hypothesis. The evidence is in the form of sample data. After you have determined which hypothesis the sample supports, a decision is made. There are two options for a decision. If the sample information favors the alternate hypothesis, we conclude, “Reject ![]() “. If the sample information is not compelling enough to reject the null hypothesis, we say, “Fail to Reject
“. If the sample information is not compelling enough to reject the null hypothesis, we say, “Fail to Reject ![]() ”.
”.
One-Tailed or Two-Tailed Tests
Consider a situation in which children have a growth hormone deficiency and a new growth hormone treatment is created. The researcher claims that children who are given this new growth hormone grow more than 4 inches per year on average. Notice how this claim is one-directional. The researcher hopes to show the mean growth in children is greater than 4 inches. This statement becomes the alternate hypothesis. In words the alternate hypothesis would state, “The mean growth per year is greater than 4 inches.” The null hypothesis then is the opposite of this statement. It negates or nullifies the alternate hypothesis. It is a statement that there is no treatment effect, so in this case, the null hypothesis would state, “The mean growth per year is less then or equal to 4 inches.” When children are randomly given the growth hormone, data is collected, and data is analyzed, the results are compared to the null hypothesis assumption that there is no effect. In this way, the null hypothesis gives us critical information from which to make a comparison. If the sample evidence is so different that one would expect if there is no treatment effect, then the conclusion must be that the evidence suggests a treatment effect exists. We call this situation a one-tailed hypothesis test.
Hypothesis tests can be one-tailed or two-tailed, depending on the research question. The two hypothesis statements together must account for all possible outcomes, so Table 1 gives the options for each hypothesis statement.
| Type of Hypothesis Test | ||
|---|---|---|
| Two-Tailed Test | Contains equal (=) | Contains not equal (≠) |
| One-Tailed Test | Contains greater than or equal to (≥) | Contains less than (<) |
| One-Tailed Test | Contains less than or equal to (≤) | Contains more than (>) |
Special Notes:
The null hypothesis, ![]() , always has a symbol with an equal in it. It is the equality part of the statement which provides a specific probability distribution against which the sample information is compared, in order to gauge whether there is evidence to support a claim. Even if the null hypothesis contains
, always has a symbol with an equal in it. It is the equality part of the statement which provides a specific probability distribution against which the sample information is compared, in order to gauge whether there is evidence to support a claim. Even if the null hypothesis contains ![]() or
or ![]() , it is the value from the equality used in the null distribution. That equality value forces the most evidence to be gathered in order to reject the null hypothesis.
, it is the value from the equality used in the null distribution. That equality value forces the most evidence to be gathered in order to reject the null hypothesis.
The alternate hypothesis, ![]() , never has a symbol with an equal in it. The choice of symbol depends on the wording of the research claim.
, never has a symbol with an equal in it. The choice of symbol depends on the wording of the research claim.
Please be aware that many researchers use = in the null hypothesis, even with > or < as the symbol in the alternative hypothesis. This practice is used because we make the decision only to reject or not reject the null hypothesis. The decision is never made to accept the null hypothesis.
Example 1 – Hypothesis Statements
For each research question, write the null and alternate hypotheses in words and in symbols, paying close attention to the population parameter under consideration.
- HEPA filters are tested for air flow velocity per minute (fpm). A manufacturer claims their new HEPA filter maintains an average air flow of more than 100 fpm. Data will be collected to test this claim.
- A drug company produces soft-mist asthma inhalers which should deliver an average of 200 puffs of medication. Consumer complaints suggest the drug company is advertising misleading information. An independent lab will test this claim.
- After a poor debate performance in 2024, Joe Biden’s approval rating dropped. Supporters suspect that over 55% of voters disapprove of his performance, so a random sample of voters will be surveyed.
Solutions:
- The alternate hypothesis would state, “The mean airflow is greater than 100 fpm.” The null hypothesis would state the opposite, so the null hypothesis would state, “The mean airflow is less than or equal to 100 fpm.” Symbolically,
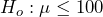 and
and 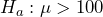 .
. - In the case of the mean number of puffs per inhaler, the consumer would be concerned if there are fewer than 200 puffs because they will not be getting the amount of drug advertised. The manufacturer would be concerned if there are more than 200 puffs because this would cost them money, so this is a two-sided test. The alternate hypothesis would state, “The mean number of puffs per inhaler is different from 200”, while the null hypothesis would state, “The mean number of puffs per inhaler is equal to 200”. Symbolically,
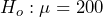 and
and 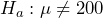 .
. - In this case, notice that the claim is not about a mean, but instead about a percentage. In sampling, voters would be asked if they approve or disapprove of President Biden, so this question has to do with the true proportion of voters who disapprove of President Biden. The alternate hypothesis would state, “The proportion of voters who disapprove of President Biden is greater than 0.55.” The null hypothesis would state, “The proportion of voters who disapprove of President Biden is less than or equal to 0.55.” Symbolically,
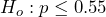 and
and 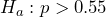 .
.
Null Distribution
If our research question leads us to gather sample data and test a hypothesis about a single population mean, then the distribution of the sample mean comes into play. If our research question leads us to gather data and test a hypothesis about a single population proportion, then the distribution of the sample proportion is needed. With means or proportions, we have seen large samples, small samples, situations for which the population standard deviation is known or can be assumed, and situations when the population standard deviation must be estimated with the sample standard deviation. Taken together, the research question, sampling technique, parameter of interest, and sampling statistic each guide us to the underlying sampling distribution. It is the sampling distribution along with the assumption that the null hypothesis is true that gives us the null distribution, a probability distribution against which we will compare sample information and judge the validity of the claim.
T-Test
Single Population Mean: When performing a hypothesis test involving a single population mean μ, under certain circumstances, the underlying sampling distribution of the statistic ![]() is the Student’s t-distribution. This is called a t-test and the standardized t-score is used as the test statistic. There are fundamental assumptions that need to be met in order for Student’s t-distribution to be used. The data should be a simple random sample that comes from a population that is approximately normally distributed and the sample standard deviation is used to approximate the population standard deviation. When these conditions are met, we have:
is the Student’s t-distribution. This is called a t-test and the standardized t-score is used as the test statistic. There are fundamental assumptions that need to be met in order for Student’s t-distribution to be used. The data should be a simple random sample that comes from a population that is approximately normally distributed and the sample standard deviation is used to approximate the population standard deviation. When these conditions are met, we have:
![]() with
with ![]() degrees of freedom, so
degrees of freedom, so ![]() and
and ![]()
Z-Tests
Single Population Mean: When performing a hypothesis test involving a single population mean μ, under certain circumstances, the underlying sampling distribution of the statistic ![]() is the normal distribution. This is called a z-test and the standardized z-score is used as the test statistic. There are fundamental assumptions that need to be met in order for normal distribution to be used. The sample must be a simple random sample from the population. The population standard deviation is known or can be assumed from prior history with the population. The population from which the sample comes is normally distributed or the sample size is sufficiently large. When these conditions are met, we have:
is the normal distribution. This is called a z-test and the standardized z-score is used as the test statistic. There are fundamental assumptions that need to be met in order for normal distribution to be used. The sample must be a simple random sample from the population. The population standard deviation is known or can be assumed from prior history with the population. The population from which the sample comes is normally distributed or the sample size is sufficiently large. When these conditions are met, we have:
![]() , so
, so ![]() and
and ![]()
What often happens is that in practice there is a large sample and the population standard deviation is unknown, so it is estimated with the sample standard deviation. In that case, the sampling distribution is only approximately normally distributed. Some are fine with that but some will switch to using the Student’s t-distribution anytime the population standard deviation is unknown.
Single Population Proportion: When performing a hypothesis test involving a single population proportion p, under certain circumstances, the underlying sampling distribution of the statistic ![]() is the binomial distribution. If there has been a simple random sample of the population, there are a certain number of
is the binomial distribution. If there has been a simple random sample of the population, there are a certain number of ![]() independent trials, the outcomes of any trial are success or failure, and each trial has the same probability of a success
independent trials, the outcomes of any trial are success or failure, and each trial has the same probability of a success ![]() . The shape of the binomial distribution needs to be similar to the shape of the normal distribution. To ensure this, the quantities
. The shape of the binomial distribution needs to be similar to the shape of the normal distribution. To ensure this, the quantities ![]() and
and ![]() must both be greater than five. This is a common rule of thumb, but a more conservative rule is to have both
must both be greater than five. This is a common rule of thumb, but a more conservative rule is to have both ![]() and
and ![]() be greater than ten. When these conditions are met, the binomial distribution of a sample proportion can be approximated by the normal distribution.
be greater than ten. When these conditions are met, the binomial distribution of a sample proportion can be approximated by the normal distribution.
![]() , so
, so 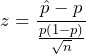 and
and ![]()
P-Value and Conclusions
The null distribution is the distribution of the sample statistic, such as ![]() or
or ![]() , under the assumption that the null hypothesis is true. This completely defines a probability distribution used for decision making. The sample information is then compared to the null distribution to assess how likely it would be for a sample such as the one observed to come from that null distribution. Through this comparison, a number between 0 and 1 is produced. This number is called the p-value. The p-value is also called the observed level of significance. The smaller the p-value, the more evidence there is to reject the null hypothesis. If the p-value is sufficiently small, then we are willing to abandon the assumption that the null hypothesis is true in favor of the claim made in the alternate hypothesis. When this happens we reject the null hypothesis.
, under the assumption that the null hypothesis is true. This completely defines a probability distribution used for decision making. The sample information is then compared to the null distribution to assess how likely it would be for a sample such as the one observed to come from that null distribution. Through this comparison, a number between 0 and 1 is produced. This number is called the p-value. The p-value is also called the observed level of significance. The smaller the p-value, the more evidence there is to reject the null hypothesis. If the p-value is sufficiently small, then we are willing to abandon the assumption that the null hypothesis is true in favor of the claim made in the alternate hypothesis. When this happens we reject the null hypothesis.
On the other hand, when the p-value is large, and how large depends on the situation, then this provides evidence against the alternate hypothesis claim. We would know that the sample would be a very usual sample from the null distribution, so we would fail to reject the null hypothesis. It is important to be careful with the wording of any conclusion. When we fail to reject the null hypothesis, we are not accepting the null hypothesis as truth. We simply did not have compelling evidence to reject the null hypothesis. Think back to the jury trial analogy. If we fail to convict a defendant of a crime, we acquit the defendant. It does not necessarily mean they are innocent. We just did not see enough evidence, beyond a reasonable doubt, to convict them.
Significance Level
When a p-value is calculated and is less then a pre-determined threshold, the result is deemed to be “statistically significant” at that pre-determined level. Often a significance level is picked to be 0.05 or 0.01 and that significance level creates a “critical region.” If a p-value is calculated and is less than 0.05, for example, then the test would be significant at the 5% level. The significance level is denoted by ![]() . While selecting a particular
. While selecting a particular ![]() significance level in advance gives a benchmark for rejecting, giving the p-value, which is the observed significance level, provides additional information.
significance level in advance gives a benchmark for rejecting, giving the p-value, which is the observed significance level, provides additional information.
In many disciplines and in research articles, it is common to see a significance level of 5% cited, although it certainly depends on the application. What would be problematic is to run a hypothesis test, observe the result, and then select a significance level so that the results are significant. Also it is important to consider statistical significance along side of practical significance. Suppose a hypothesis test showed a newly designed lightbulb has a mean increase in lifetime of 6 days compared to previous lightbulbs and this result is significant at the 0.05 level. While this result is statistically significant, is it practically significant to bring a new product to scale, including advertising, etc., for only an additional 6 days of average lifetime?
Videos
YouTube Video Khan Academy Simple Hypothesis Testing
Sources
Higuera, V. (2023, November 20). What do growth hormone injections do? https://www.medicalnewstoday.com/articles/312905#injections
Silver, N. (2024, July 18). How popular is Joe Biden? FiveThirtyEight. https://projects.fivethirtyeight.com/biden-approval-rating/
Tenny, S., & Abdelgawad, I. (2023, November 23). Statistical significance. StatPearls – NCBI Bookshelf. https://www.ncbi.nlm.nih.gov/books/NBK459346/


Feedback/Errata