11.2 One-Way ANOVA Overview

So far we have tested claims about means from one or two populations. When we compared two groups, we likely used a t-test. In that case, there was often a group affected by a treatment and another group unaffected by a treatment. The goal was to see if the means were significantly different. This concept can be extended to several groups when we consider multiple levels of a treatment. With more samples, a treatment can be applied to each sample and the means can be compared. However a t-test will not be appropriate when multiple groups are considered. We will need a new way to analyze the situation. We will use a new method called the Analysis of Variance to extend the comparison that can be made from two groups to several groups. Analysis of variance is abbreviated ANOVA.

We will use the analysis of variance to compare mean responses from three or more samples, with a treatment applied to each. The treatments are different levels of a single factor under consideration, so this means we will be conducting One-Way Analysis of Variance. The one-way ANOVA is a type of experimental design called a factorial experiment, in which one factor is considered at multiple levels or treatments. Then a response variable is measured on each of the experimental units. Ultimately the question we try to address with this type of experiment is whether varying the levels of the factor will produce a difference in the mean of the response variable. Clearly we have new vocabulary to to learn with ANOVA, so it might help to consider an experiment to put the vocabulary into context.

Consider a situation in which a researcher would like to compare five fever-reducing treatment options: placebo, aspirin, Anacin, Tylenol, and Bufferin. Through random sampling, thirty-five people will be selected to participate in the study and seven people will be assigned to each of the five groups. The seven people in each group will be given a single treatment. This means that all seven people in one group will take aspirin. All seven people in another group will take Tylenol, etc.  Then each of the thirty-five people will have their temperature measured two hours later.

Factor Variable: Drug Type  (Notice this is a categorical variable.)
Level: placebo, aspirin, Anacin, Tylenol, and Bufferin (These are also called treatments.)
Response Variable: Body Temperature (Notice this is a numeric measured variable.)
Experimental Unit: Each of the thirty-five people. (There are seven replicates in each group.)

When designing this type of experiment, the levels of the factor variable are deliberately chosen by the researcher. This makes it a fixed-effects model, which is the type of one-way analysis of variance we will consider. When the experimental units are assigned to treatments at random, then this is a completely randomized experiment. In this type of experiment, it is appropriate to think of the group receiving a level of the treatment as coming from one population and the group receiving a different level as coming from another population. In order to make any formal statement about treatment effect, a hypothesis test will be needed.

We might initially think that we do not need any new tests because we have already learned how to compare two groups using the -test, so why not just to do several pairwise comparisons? For example, if there were three groups, we might be tempted to compare the first mean with the second, then with the third, and then finally compare the second and third means for a total of three comparisons. However, this strategy can be treacherous. If we have many groups and do many comparisons, it is likely that we will eventually find a difference just by chance, even if there is no difference in the populations. Instead, we should apply a test to check whether there is evidence that at least one pair of groups are in fact different and this is where ANOVA begins!

Assumptions

The purpose of a one-way ANOVA test is to determine the existence of a statistically significant difference among several group means. The test actually uses variances to help determine if the means are different. In order to perform a one-way ANOVA test, there are five basic assumptions to be fulfilled:

1. Each population from which a sample is taken is assumed to be normal.
2. All samples are randomly selected and independent.
3. The populations are assumed to have equal standard deviations (or variances).
4. The factor of interest is a categorical variable.
5. The response collected is a measured numerical variable.

The Null and Alternative Hypotheses

One-way analysis of variance can be used to test for the equality of means from different populations, where .

Because all the analysis takes all the groups into consideration at the same time, if there is a difference between the means, the test can indicate only that a difference exists. The test cannot point to the group with the difference. So the alternate hypothesis would reflect this.

: At least one population mean is different from the others.

Test Statistic: T-Test Versus F-Test

We used the t-test statistic when we wanted to examine the difference between the means of two groups. The t-test statistic used the sample mean difference and the standard error of the sample mean difference, so it examined the difference between two groups relative to the spread. Under the assumption that the null hypothesis was true, the test statistic had a Student’s t-distribution.

We will use a new test statistic, called the F-test statistic, now because we are comparing more than two groups and the analysis is a bit different. This new F-test statistic will use the variability of sample means (the explained variance) to an estimate of error variance (the unexplained variance). The F-test will examine a ratio of these measures of variance. Because this is a completely different type of test statistic, it has a completely different sampling distribution, called the F-distribution. It is important to keep in mind that by examining the variances, this test can only tell if there is a difference. It cannot tell exactly which groups are different.

Figure 2 shows two sets of box plots, each representing the comparison of three groups, with the group means indicated by a horizontal line through the boxes.

• In Figure 2, the three boxplots labeled (a), show a situation in which the null hypothesis is true. In this case, all means are the same, so 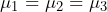. Any differences in the means are due to random variation. In this case the variance of the combined data is approximately the same as the variance of each of the populations. A test statistic which compares two measures of variation in a fraction would produce a value close to one, when the null hypothesis is true.
• In the three boxplots labeled (b), the means are not all the same, so it shows the situation in which the null hypothesis is false. The differences in the means is too large to be due to random variation alone, so the null hypothesis would be rejected. A test statistic which compares two measures of variation would find more variation among the means, and if that measure of variation is in the numerator of the F-test statistic, then the fraction would produce a value greater than one. The greater the variation in the means, the larger the F-test statistic will be. If the null hypothesis is false, then the variance of the combined data is larger due to the different means.

In the next section, we will introduce a few details about the F-distribution and will learn how to use the F-test statistic to test how likely observed differences in sample means could have happened just by chance even if there was no difference in the respective population means.

Videos

YouTube Video One-Way ANOVA