Exercise Answers

Morgan Chase

Exercise Answers

Module 1: Order of Operations

7
13
7
13
2
8
18
6
25
49
80
31
28
67
22
4
160
19
2
12
40
200
2
14
9 ∙ 2 + 30 = 48°F
(72 − 30) ÷ 2= 21°C

Module 2: Negative Numbers

5
5
−15
−22
4
−4
−9
9
18°F
3
−200
3
−3
−7
−7
7
7
3
−3
55
55
11,123 ft
543 ft
−12
−40
18
21
4
−8
16
−32
−7
−4
9
0
0
undefined
19
−73
1
−6
−8
40

Module 3: Decimals

If you’ve seen Modules 5 & 6, don’t worry about accuracy or precision on these exercises.

90.23
7.056
16.55
184.015
8.28
15.756
4,147
414.7
41.47
4.147
65,625
65.625
6.5625
$656.25
243.5
2,435
243,500
24.35
6,000
6,380
0.71
0.715
$3.67 per month
7.5 miles per hour

Module 4: Fractions

$\frac{11}{30}$
$\frac{19}{30}$
$\frac{12}{15}$
$\frac{8}{12}$
7
1
0
undefined
$\frac{3}{4}$
$\frac{5}{3}$
2
$\frac{1}{2}$
$\frac{5}{12}$
1
at least 45 questions
16
$\frac{3}{5}$
6 scoops
A requires $\frac{1}{12}$ cup more than B
$\frac{1}{2}$ of the pizza
$\frac{2}{3}$ more
$\frac{5}{8}$ inches combined
$\frac{1}{8}$ inches difference
$\frac{7}{12}$ combined
$\frac{1}{12}$ more
2.75
0.35
$0.\overline5$ or 0.555…
$1.\overline{63}$ or 1.636363…
$11\frac{1}{2}$
$4\frac{2}{3}$
$\frac{11}{5}$
$\frac{20}{3}$
$10\frac{3}{8}$
$4\frac{7}{8}$
$8\frac{1}{6}$
$1\frac{5}{6}$ cup

Module 5: Accuracy and Significant Figures

exact value
approximation
exact value
approximation
exact value
approximation
three significant figures
four significant figures
five significant figures
two significant figures
three significant figures
four significant figures
two significant figures; the actual value could be anywhere between 28,500 and 29,500
three significant figures; the actual value could be anywhere between 28,950 and 29,050
four significant figures; the actual value could be anywhere between 28,995 and 29,005
five significant figures; the actual value could be anywhere between 28,999.5 and 29,000.5
51,800
51,840
4.3
4.28
14,000
$14,\overline{0}00$
2.6
2.60
29,000 ft
$29,\overline{0}00$ ft
29,030 ft
29,032 ft
29,031.7 ft
107
640
14.4
12
$23

Module 6: Precision and GPE

thousands
hundreds
tens
thousandths
ten thousandths
hundred thousandths
82,000
$82,\overline{0}00$
$82,0\overline{0}0$
0.6
0.60
0.600
39.3 lb
39 lb
$9,800
$$8\overline{0}0$
thousands place; the nearest 1,000 people
±500 people
hundred thousandths place; the nearest 0.00001 in
±0.000005 in
hundredths place; the nearest 0.01 mil
±0.005 mil
$30\overline{0}$ miles
ones place; the nearest 1 mile
±0.5 mi
ones place; the nearest 1 minute
±0.5 min
two sig figs
three sig figs
55 mi/hr
When dividing, we must round the result based on the accuracy; i.e., the number of significant figures.

Module 7: Formulas

$2.70 (oops—the print edition says $2.46)
$4.14
$17.80
$24.80
$3.80
6 representatives
10 representatives
52 representatives
8 electoral votes
12 electoral votes
54 electoral votes
≈ 115°F; the official record high in the city was 116°F.
37°C
−0.4°F
200°C
90 mm Hg
around 107 mm Hg
70 in
74 in
yes
no; too large
no; too small
yes

Module 8: Perimeter and Circumference

70 ft
58 cm
28 cm
104 ft
130 ft
56 ft
24 in
$2\overline{0}$ cm (the print textbook says 20 cm, which implies only one sig fig…)
28.3 in
18.8 cm
44.0 ft
53 m

Module 9: Percents Part 1

47%
53%
$\frac{71}{100}$
$\frac{1.3}{100}=\frac{13}{1000}$
$\frac{0.04}{100}=\frac{1}{2500}$
$\frac{106}{100}=\frac{53}{50}$
0.71
0.013
0.0004
1.06
23%
7%
8.5%
250%
28%
12.5%
31.5
22.5
67.5
100
38.6
2.25
$9.35
$119.32

Module 10: Ratios, Rates, Proportions

$\frac{3}{8}$
$\frac{105\text{ mi}}{2\text{ hr}}$
$\frac{52.5\text{ mi}}{1\text{ hr}}$ or 52.5 miles per hour
≈ $0.335/oz, or 33.5¢/oz

Carmella Creeper parties like it’s 1995.
≈ $0.281/oz, or 28.1¢/oz
≈ $0.281/oz, or 28.1¢/oz
$\frac{3}{4}=\frac{3}{4}$; true
$\frac{2}{3} \neq \frac{4}{5}$; false
168 = 168; true
200 ≠ 240; false
70 ≠ 60; false
20 = 20; true
x = 12
n = 5
k = 4
w = 10
x = 10.4
m = 2.0
256 miles
20 hours
≈ 50 miles (rounding to one sig fig seems like a good idea here)
190 pixels wide

Module 11: Scientific Notation

Earth’s mass is larger because it’s a 25-digit number and Mars’ mass is a 24-digit number, but it might take a lot of work counting the zeros to be sure.
Earth’s mass is about ten times larger, because the power of 10 is 1 higher than that of Mars.
A chlorine atom’s radius is larger because it has 9 zeros before the significant digits begin, but a hydrogen atom’s radius has 10 zeros before the significant digits begin. As above, counting the zeros is a pain in the neck.
The chlorine atom has a larger radius because its power of 10 is 1 higher than that of the hydrogen atom. (Remember that −10 is larger than −11 because −10 is farther to the right on a number line.)
$100,000; $1.00000 \times 10^5$
$999,999; $9.99999 \times 10^5$
$1.234 \times 10^3$
$1.02 \times 10^7$
$8.70 \times 10^{-4}$
$7.32 \times 10^{-2}$
35,000
90,120,000
0.00825
0.000014
$8 \times 10^7$
$3.5 \times 10^{13}$
$6 \times 10^{-5}$
$4.8 \times 10^5$
1,260 people per square mile
250 people per square mile
the proton’s mass is roughly 1,830 or $1.83 \times 10^3$ times larger
$335.9 \times 10^6$; $3.359 \times 10^8$
$8.020 \times 10^9$; $8.020 \times 10^9$
$33.9 \times 10^{12}$; $3.39 \times 10^{13}$
≈ $101,000 per person

Module 12: Percents Part 2 and Error Analysis

93% or 93.3%
37.5%
$2,500
720
93% or 93.3%
37.5%
$2,500
720
44.8% or 45%
50 grams of added sugars is the recommended daily intake for a 2,000 calorie diet.
56% increase
10.1% sales tax
36% decrease
2.7% decrease
0.1875 ÷ 25 ≈ 0.75%
0.13 ÷ 10.8 ≈ 1.2%
4.806 g; 5.194 g
3.88%
5.443 g; 5.897 g
4.00%

Module 13: The US Measurement System

We generally won’t worry about significant figures in these answers; we’ll probably say “2 miles” even if “2.000 miles” is technically correct.

54 in
54 ft
36 in
1,760 yd
$14\frac{2}{3}$ ft or 14 ft 8 in
15 yd
2 mi
30 yd
40 oz
2,400 lb
18.75 lb
32,000 oz
48 fl oz
7 pt
8 pt
5 c
1.25 gal
64 fl oz
3 lb 7 oz
7 c 3 fl oz
15 ft 2 in
4 t 500 lb
20 lb or 20 lb 0 oz combined
3 lb 2 oz heavier
9 ft 1 in combined
1 ft 5 in longer

Module 14: The Metric System

5 m
28 cm
3.8 km
1.6 m
160 cm
3 mm
536 cm
5,360 mm
1,609 m
160,900 cm
0.297 m
29.7 cm
0.828 km
82.8 dam
100 g
80 kg
500 mg
2,000 kg
2,270 g
2,270,000 mg
6,500 cg
65,000 mg
0.065 kg
9.5 cg
0.095 g
50 L
30 mL
0.5 L
10.5 dL
1,750 mL
0.25 L
they are equal in size
about 11 to 1
4 bottles; this is easier if you know that a 500-milliliter bottle of Mexican Coke is called a medio litro.

Doce litros de Coca-Cola

Module 15: Converting Between Systems

We may round some of these answers to three significant figures even if the given number has fewer than three sig figs. On the other hand, you’ll see that some of these answers include a critique of a manufacturer’s decision to round numbers a certain way.

31 mi
183 cm
164.0 ft
yes, 4 in = 101.6 mm according to the conversion, but is it really 4.000 in to begin with? Rounding the result to 100 mm or 102 mm seems reasonable.
20 in converts to around 50.8 cm, and 50.0 cm converts to around 19.7 in. It looks like somebody used the conversion 1 in = 2.5 cm, which is fine if you’re estimating but not if you’re going to report a number to three sig figs.
not exactly but they’re pretty close; the error is around 0.4%. (oops—the print edition says 0.3%)
yes; using either conversion gives a result of 294.8 kg, rounded to the nearest tenth. However, it doesn’t make sense for this to be accurate to four sig figs. It would be best to round to 295 or perhaps even $3\overline{0}0$ kg.
not exactly; using 1 kg ≈ 2.205 lb gives a result of 1,473.9 kg, and using 1 lb ≈ 0.4536 kg gives a result of 1,474.2 kg. Again, the accuracy here doesn’t make sense, especially when you consider that the numbers on the box don’t agree with each other: 294.8 ∙ 5 ≠ 1,474.1.
11 lb
≈ 230 g
≈ 110 g
≈ 1.8 oz
about $1.09
about $0.99
≈ 1.3 gal
355 mL
3.4 fl oz
no matter which conversion you use, the result should round to 22.7 liters.
a bit less than 600 km
11 km/L

Module 16: Other Conversions

We will generally round these answers to three significant figures; your answer may be slightly different depending on which conversion ratio you used.

525,600 min; if you’re familiar with the musical Rent, then you already knew the answer.
this is roughly 31.7 years, which is indeed possible
37.6 km/hr
23.3 mi/hr
1,770 mi/hr
29.5 mi in 1 min
20.3 min
0.17 mi/gal
5.8 gal/mi
171 gal in 1 min
the capacity increased by a factor of 14.4
4 times greater
1,200 watts per home, or 1.2 kilowatts per home (oops—the print edition says 1,200 megawatts)
1 watt per gallon
2,500 times more powerful
0.4 ms, 0.04 ms, 0.004 ms; 400 μs, 40 μs, 4 μs
the ratio of the wavelengths of red and infrared is 7 to 100;
the ratio of the wavelengths of infrared and red is around 14 to 1
this is equivalent to 2,500 chest x-rays

Module 17: Angles

right angle
obtuse angle
reflexive angle
straight angle
acute angle
a = 127°; b = 53°; c = 127°
27°
97°
23° each
45° each
60° each
A = 61°; B = 80°; C = 39°
18.9111°
155.6808°
34.1924°
29° 58′ 30”
31° 8′ 15”
76° 20′ 48.1”

Module 18: Triangles

right isosceles triangle
obtuse scalene triangle
acute equilateral triangle (yes, an equilateral triangle will always be acute)
w = 35 ft
x = 8 cm; y = 10.5 cm
d = 268 ft
n = 55 cm
this is a right triangle, because $5^2+12^2=13^2$.
this is not a right triangle, because $8^2+17^2\neq19^2$.
7.07
17.20
30.71
10 ft
15 ft
12.3 cm
1.8 cm

Module 19: Area of Polygons and Circles

We may occasionally include extra sig figs in these answers so you can be sure that your answer matches ours.

$20\text{ cm}^2$
$16\text{ cm}^2$
$4.86\text{ m}^2$
$12.25\text{ ft}^2$
$120\text{ in}^2$
$360\text{ m}^2$
$210\text{ ft}^2$
$126\text{ cm}^2$
$38.5\text{ cm}^2$
$204\text{ ft}^2$
$2,160\text{ in}^2$
$36\text{ m}^2$
$124\text{ cm}^2$
$192\text{ cm}^2$
$28.3\text{ cm}^2$
$220\text{ m}^2$
$154\text{ ft}^2$
$63.6\text{ in}^2$

Module 20: Composite Figures

$64\text{ ft}$
$189\text{ ft}^2$
$590\text{ cm}^2$; the area of the rectangle is $800\text{ cm}^2$ and the areas of the triangles are $70\text{ cm}^2$ and $140\text{ cm}^2$.
$590\text{ cm}^2$; hey, that’s what we got for #3!
$148\text{ m}$
$940\text{ m}^2$
Based on the stated measurements, the distance around the track will be 401 meters, which appears to be 1 meter too long. In real life, precision would be very important here, and you might ask for the measurements to be given to the nearest tenth of a meter.
around $9,620\text{ m}^2$
$1,960\text{ cm}^2$
$178.5\text{ cm}$
$29\text{ ft}^2$
23.5 ft (oops—the print edition says 47 ft)
around 21.5% (Hint: Make up an easy number for the side of the square, like 2 or 10.)
around 36.3% (Hint: The diagonals of the square are equal to the circle’s diameter.)

Module 21: Converting Units of Area

We may occasionally include extra sig figs in these answers so that you can be sure that your answer matches ours.

$162\text{ ft}^2$
$162\text{ ft}^2$
$7\text{ ft}^2$
$7\text{ ft}^2$
$7,776\text{ in}^2$
$8.3\text{ ac}$
$180,000\text{ cm}^2$
$180,000\text{ cm}^2$
$623.7\text{ cm}^2$
$623.7\text{ cm}^2$
$6\text{ m}^2$
$4\text{ ha}$
$376\text{ km}^2$
$2,\overline{0}00\text{ ha}$, rounded to two sig figs
$603\text{ cm}^2$
$75,300\text{ ft}^2$, rounded to three sig figs
$154\text{ in}^2$
$38.5\text{ in}^2$
4 to 1; if we double the linear measurement, we get four times the area.
$54\text{ cm}^2$
$6\text{ cm}^2$
9 to 1; if we triple the linear measurement, we get nine times the area.

Module 22: Surface Area of Common Solids

$36\text{ cm}^2$
$76\text{ cm}^2$
$471\text{ cm}^2$
$628\text{ cm}^2$
$616\text{ cm}^2$
$380\text{ in}^2$

Module 23: Area of Regular Polygons

All answers have been given to two or three significant figures.

$6,900\text{ in}^2$
$94\text{ cm}^2$
$750\text{ in}^2$
$751\text{ mm}^2$
$480\text{ cm}^2$
$110\text{ m}^2$
$280\text{ mm}^2$ (the area of the circle $\approx1,660\text{ mm}^2$ and the area of the hexagon is $1,380\text{ mm}^2$)

Module 24: Volume of Common Solids

$40\text{ cm}^3$
$531\text{ cm}^3$
$45\text{ cm}^3$
$350\text{ cm}^3$
$520\text{ cm}^3$
$22,600\text{ ft}^3$
$3.7\text{ mm}^3$
$1,440\text{ cm}^3$
$697\text{ in}^3$ or $7\overline{0}0\text{ in}^3$
$22.7\text{ cm}^3$ (the cylinder’s volume $\approx14.1\text{ cm}^3$ and the hemisphere’s volume $\approx8.6\text{ cm}^3$.)
$37.6\text{ ft}^3$ (the cylinder’s volume $\approx29.45\text{ ft}^3$ and the two hemispheres’ combined volume $\approx8.18\text{ ft}^3$)
$37.6\text{ ft}^3$ ≈ 282 gal, which is more than 250 gal.

Module 25: Converting Units of Volume

the result is very close to 1 cubic yard: (112 in ∙ 14 in ∙ 10 in) ∙ 3 crates = 47,040 in³ ≈ 1.01 yd³
this estimate is also 1 cubic yard: (9 ft ∙ 1 ft ∙ 1 ft) ∙ 3 crates = 27 ft³ = 1 yd³
around 60 gallons
yes, the can is able to hold 12 fluid ounces; the can’s volume is roughly 23.3 in³ ≈ 12.9 fl oz.
5 gallons
around 2,300 to 2,400 liters; a calculator says 2,356 liters which should technically be rounded up to 2,400 liters, but it would be reasonable to round down to 2,300 liters instead if you considered the volume of the benches and the fact that the sides might slope inwards near the bottom of the tub.
the rectangular section of the carton has a volume of 1.7 liters, which is larger than the required 1.5 L.
≈ 21 cm high

Independent verification from my kitchen.
$19.6\text{ yd}^3$
$53\overline{0}\text{ ft}^3$
$1.53\text{ m}^3$
$327\text{ in}^3$
$5,350\text{ cm}^3$
5.35 L
$0.5\text{ ft}^3\approx14.16\text{ L}$; assuming that it’s 0.50 ft³, these measures are equivalent to two sig figs.
$100\text{ lb/ft}^3$
31 lb; now you can laugh whenever you see someone in a heist movie load a cheap duffel bag with gold bars and carry it out of the vault.
1.1 kg
$268\text{ cm}^3$
$33.5\text{ cm}^3$
8 to 1
$1,620\text{ in}^3$
$60\text{ in}^3$
27 to 1

Module 26: Pyramids and Cones

$1,280\text{ cm}^3$
$2,420,000\text{ m}^3$
$544\text{ cm}^2$; $80\overline{0}\text{ cm}^2$
$82,300\text{ m}^2$
$310\text{ cm}^3$ (if we had greater accuracy, the result would be 314.16 because it’s 100 times $\pi$.)
$38\text{ ft}^3$
$47\text{ ft}^2$; $75\text{ ft}^2$
$2\overline{0}0\text{ cm}^2$; $280\text{ cm}^2$

Module 27: Percents Part 3

$1,299.00
14,861 students; notice that if the percent had fewer than five sig figs, we wouldn’t have been able to get an answer that was accurate to the nearest whole number.
Yes, you can! Each bottle cost $3.59.

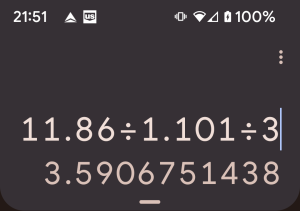
Real time screenshot of my phone’s calculator.
$3.20 million
873,900 people
$16; the percent has only two sig figs, so it doesn’t make sense to assume that the price was $16.13. They probably rounded the percent from 68.75% to make the numbers in the advertisement seems less complicated.

Module 28: Mean, Median, Mode

10.3 min
$4.488
11.0 min (because it is the seventh value in the list of thirteen)
$4.475
$256,000
$250,000
$338,000
$275,000
the median is more representative because the mean is higher than five of the six home values.
11.0 min (because it appears four times in the list)
no mode (there are no repeated values)
AT&T Mobility
Samoas and Thin Mints
12.2 games
12 games
12 games
they all represent the data fairly well; 12 wins represents a typical Patriots season.
6.8 games
7 games
6 games
they all represent the data fairly well; 6 or 7 wins represents a typical Bills season.
98.2 grams; the mean doesn’t seem to represent a typical clementine because there is a group of smaller ones (from 82 to 94 grams) and a group of larger ones (from 102 to 109 grams) with none in the middle.
94 grams; for the same reason, the median doesn’t represent a typical clementine, but you could say it helps split the clementines into a lighter group and a heavier group.
no mode; too many values appear twice.
98.3 grams; this is a small increase over the previous mean.
94 grams; the median does not change when one of the highest numbers increases.
109 grams; you might say it represents the mass of a typical large clementine, but it doesn’t represent the entire group.

Module 29: Probability

$\frac{6}{36}=\frac{1}{6}$
$\frac{2}{36}=\frac{1}{18}$
$\frac{8}{36}=\frac{2}{9}$
$\frac{36}{36}=1$
$\frac{0}{36}=0$
$\frac{4}{36}=\frac{1}{9}$
$\frac{32}{36}=\frac{8}{9}$
$\frac{6}{36}=\frac{1}{6}$
$\frac{30}{36}=\frac{5}{6}$
$\frac{15}{60}=\frac{1}{4}=0.25=25\%$
$\frac{45}{60}=\frac{3}{4}=0.75=75\%$
$\frac{18}{60}=\frac{3}{10}=0.3=30\%$
$\frac{42}{60}=\frac{7}{10}=0.7=70\%$
$\frac{1}{4}=25\%$
$\frac{3}{4}=75\%$
$\frac{2}{4}=50\%$
$\frac{2}{4}=50\%$
$\frac{8}{250}=3.2\%$
$\frac{242}{250}=96.8\%$
we should expect 968 copies to be acceptable
$\frac{44}{200}=22\%$
we should expect 220 tax returns to have errors
22% = 0.22
$(0.22)^2\approx4.8\%$
$(0.22)^3\approx1.1\%$
$0.22\cdot0.78\approx17.2\%$
$0.78\cdot0.22\approx17.2\%$
$(0.78)^2\approx60.8\%$
$(0.78)^3\approx47.5\%$
$1-(0.78)^3\approx52.5\%$

Module 30: Standard Deviation

60.5; 66.5
57.5; 69.5
54.5; 72.5
66.5; 72.5
63.5; 75.5
60.5; 78.5
68% because 100% − (16% + 16%) = 68%
195 lb because this is halfway between 160 and 230 lb
35 lb because 195 − 35 lb and 195 + 35 lb encompasses 68% of the data
125; 265
8.8; 15.6
You would not have predicted this from the data because it is more than two standard deviations below the mean, so there would be a roughly 2.5% chance of this happening randomly. In fact, (12.2 − 7) ÷ 1.7 is slightly larger than 3, so this is more than three standard deviations below the mean, making it even more unlikely. (You might have predicted that the Patriots would get worse when Tom Brady left them for Tampa Bay, but you wouldn’t have predicted only 7 wins based on the previous nineteen years of data.)
3.4; 10.2
You would not predict this from the data because it is more than two standard deviations above the mean, so there would be a roughly 2.5% chance of this happening randomly. In fact, (13 − 6.8) ÷ 1.7 ≈ 3.6, so this is more than three standard deviations above the mean, making it even more unlikely. This increased win total is partly due to external forces (i.e., the Patriots becoming weaker and losing two games to the Bills) but even 11 wins would have been a bold prediction, let alone 13.
3.9; 14.3
The trouble with making predictions about the Broncos is that their standard deviation is so large. You could choose any number between 4 and 14 wins and be within the 95% interval. (9.1 − 5) ÷ 2.6 ≈ 1.6, so this is around 1.6 standard deviations below the mean, which makes it not very unusual. Whereas the Patriots and Bills are more consistent, the Broncos’ win totals fluctuate quite a bit and are therefore more unpredictable.

Module 31: Right Triangle Trigonometry

the adjacent side is e, the opposite side is f, and the hypotenuse is d.
the adjacent side is x, the opposite side is y, and the hypotenuse is r.
$\frac{3}{5}=0.6$
$\frac{4}{5}=0.8$
$\frac{3}{4}=0.75$
$\frac{4}{5}=0.8$
$\frac{3}{5}=0.6$
$\frac{4}{3}\approx1.333$
0.6000
0.8000
0.7500
0.8000
0.6000
1.333
z ≈ 4.6 cm
g ≈ 2.6 cm
b ≈ 5.706 in
p ≈ 75.51 mm
y ≈ 136.18 mm
d ≈ 296.87 mm
the wire is approximately 27 ft long
≈ 17.85 ft, which is roughly 17 ft, 10 in
No; $64\cdot\text{tan }1°\approx1.1\text{ ft}$, so the puck will hit the fabric over 1 foot away from the center of the hole. (The person in the photo was given a bunch of pucks and 30 seconds to score, but he scored on his first shot. Boston Bruins at Vancouver Canucks, February 24, 2024.)
36.87°
60°
53.13°
$\angle A\approx36.47°$
$\angle 1\approx42.03°$
$\angle 1\approx30.76°$
$\angle y\approx52.88°$
$\angle 1\approx55.28°$
$\angle x\approx31.50°$; $\angle y\approx58.50°$
$\text{tan}^{-1}\left(\frac{4}{1}\right)\approx76°$ angle of elevation
Yes; $\text{sin}^{-1}\left(\frac{2}{25}\right)\approx4.59°$, which is less than $4.75°$.
$\text{tan}^{-1}\left(\frac{17}{14}\right)\approx50.5°$
$17\div\text{sin }51°\approx22.0$
$14\div\text{cos }51°\approx22.0$
$\sqrt{14^2+17^2}\approx22.0$
All three answers are the same rounded to three significant figures. This is true because we rounded $\angle A$ to the nearest tenth; if we had rounded it to 51° instead of 50.5°, we would have decreased the accuracy of #36 & #37 to only two sig figs and the three results all would have been slightly different.
≈ 23°
≈ 8,900 ft

Module 32: Slope

0.36 : 12, 0.03, 3%
0.60 : 12, 0.05, 5%
1.00 : 12, 0.0833, 8.33%
2.16 : 12, 0.18, 18%
1.72°
2.86°
4.76°
10.20°
0.5 ft
1 ft
5 ft
$\text{tan}^{-1}\left(20/12\right)\approx59°$ from vertical. (this would be an angle of depression of 31°.)
30 ft; the proportion $\frac{1}{12}=\frac{2.5}{x}$ gives a result of exactly 30 ft.
Using the result from #7, the equation $\text{tan}\left(4.76°\right)=\frac{2.5}{x}$ gives a result very close to 30.0 ft.

Module 33: Non-Right Triangle Trigonometry

k ≈ 61 in
a = c = 74°; x ≈ 5.168 in
x ≈ 11.6 cm; y ≈ 12.3 cm
the shorter wire is roughly 23.5 feet; the longer wire is roughly 26 feet.

Exercise 4 is based on actual events!
n ≈ 72.4°
n ≈ 107.6°
d ≈ 65 mm
p ≈ 11.4 cm
w ≈ 14.12 m
the distance across the pond is roughly 81.5 meters.
X ≈ 19.4°; Y ≈ 133.5°; Z ≈ 27.1°

Module 34: Radian Measure

$\frac{\pi}{6}$
$\frac{\pi}{4}$
$\frac{\pi}{3}$
$\frac{\pi}{2}$
$\frac{2\pi}{3}$
$\frac{5\pi}{4}$
$\frac{4\pi}{3}$
$\frac{3\pi}{2}$
15°
135°
150°
315°
≈ 57.3°

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License