4 Modeling Tendon Elasticity
Modeling Tendon Elasticity
Materials:
- writing utensil
- calculator
- digital device with spreadsheet program
- digital device with internet access
Objectives
- Identify regions and features of the stress vs. strain curve.
- Analyze the features of the stress vs. strain curve to assess qualitative material properties.
- Analyze stress vs. strain data to determine ultimate strength and elastic modulus.
- Compare and contrast stress vs. strain curves and material properties in the context of real-world applications.
Qualitative Characterization MEthods
Modeling Methods
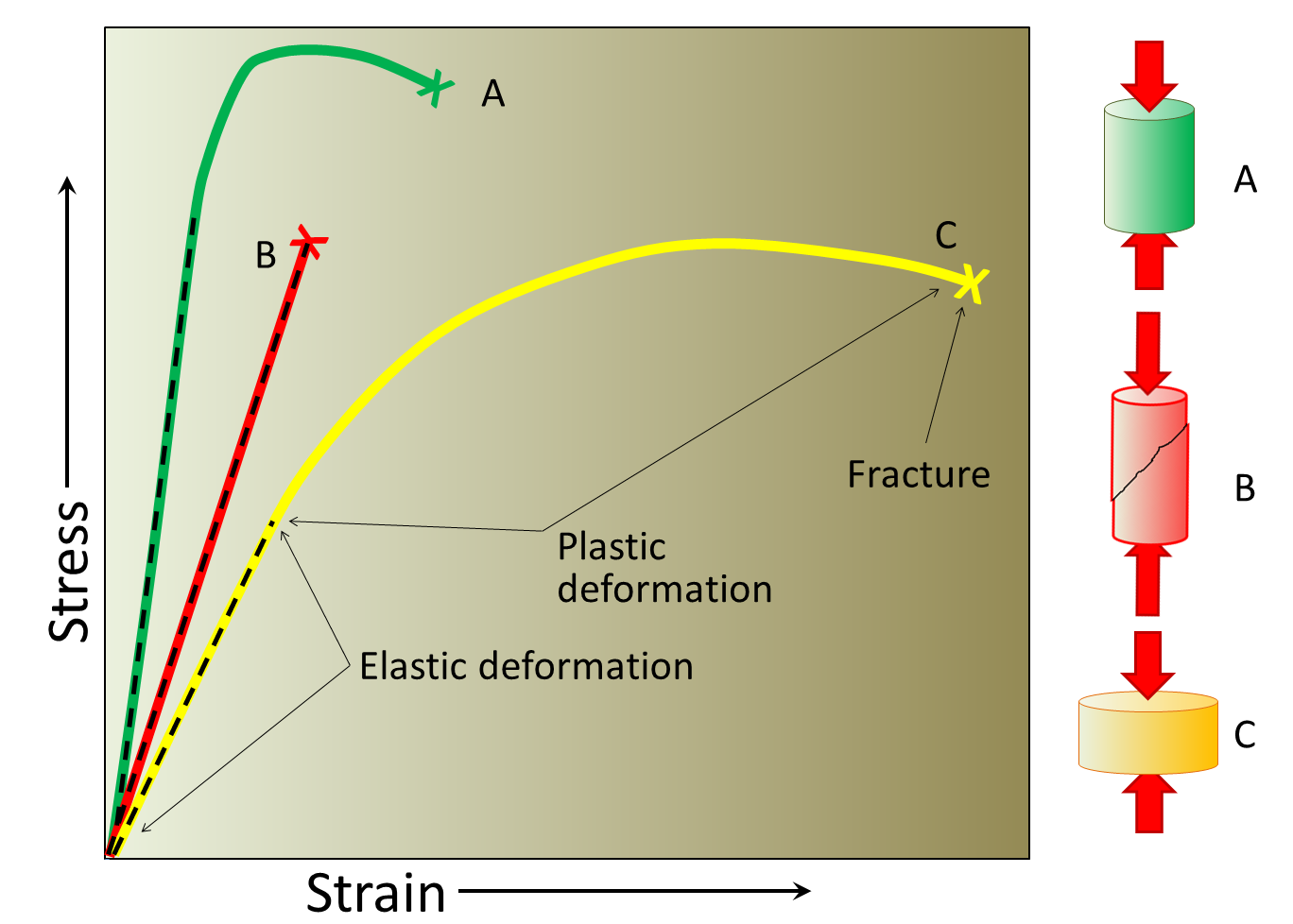
Materials can be categorized as brittle or ductile based on the relative size of their linear and failure regions. A brittle material will fracture or rupture very shortly after reaching the yield point, the point at which the material begins to permanently deform. A ductile material will have a relatively long failure region, corresponding to permanent deformation without fracture or rupture.
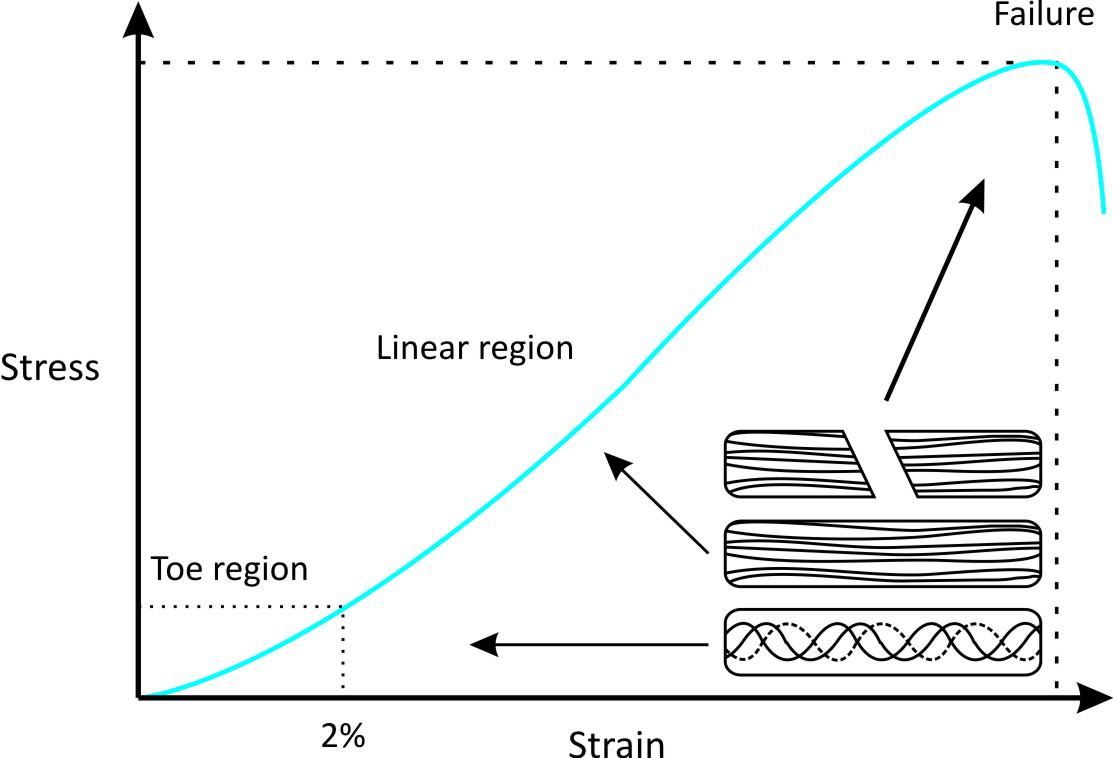
Some materials stretch easily up to a certain point, but then become very stiff and difficult to stretch. This behavior causes a toe region in their stress vs. strain curves. For example, the stress vs. strain curves of tendons exhibit a toe region do to crimping behavior.
Experimental Methods
Data Collection Methods
The materials tester in the video provides the tension force and the displacement (stretch). That data is available in an online spreadsheet. You can copy and paste the data into your own spreadsheet for analysis. The data in the spreadsheet, and the graph in the video are not the stress vs. strain curve. Stress and strain need to be calculated by following the steps in the rest of the lab.
Data Analysis Methods
Stress and Strain
To calculate stress we will need to know the original cross-sectional area of the rubber band. We will assume the band does not thin out as it stretches so we will use the original cross section to calculate the stress throughout the experiment. The stress calculated using this approximation is known as the engineering stress. The original diameter of the hair tie was measured to be 2.4 mm using calipers (see image below).

1) Calculate the cross-sectional area of the hair tie in units of m2. Show your work.
2) The hair-tie was looped around the quick-links in the materials tester, so we were actually stretching two strands of the hair tie throughout the experiment. Therefore, the cross sectional area being stretched was actually double what you just calculated above and we need to use the doubled value in calculating the stress on the material. Record the actual cross sectional area that we will use in calculating stress:
3) To calculate strain we need to know the original length of the hair tie before any additional force is applied by the apparatus. (The force applied due to the weight of the couplings is not measured by the apparatus, so we have measured the original length with the couplings in place, which allows us to record only the additional stretch caused by the additional force applied by the apparatus. That length (between inside edges at top and bottom) is 2.2 cm

4) Paste the Force and Displacement data into your spreadsheet. Follow the steps in the video below to calculate the stress and strain.
5) Plot the stress on the vertical axis and strain on the horizontal axis. Be sure to title your graph and enter axes labels with correct units.
Elastic Modulus (Young’s Modulus)
6) The elastic modulus of the material is defined as the __________ of the graph in the __________ region of the stress vs. strain curve.
7) Create a second plot that only contains the data from the linear region. Fit a line to this data and record the fit equation and the R2 here:
8) What is the elastic modulus of the hair-tie material?
9) What is the elastic modulus in units of MPa and also in units of GPa?
Ultimate Strength
10) Use your graph or examine your data direction to find the maximum stress before failure. This is known as the _________strength. What is this value in units of MPa and also in units of GPa?
Conclusions
11) Does the hair tie stress vs. strain curve contain a toe region, and if so, what range of strain values does it cover? Explain how you decided on the range. [Hint: Compare the stress strain curve with those shown and described in the Qualitative Characterization Methods section at the beginning of the lab.]
12) Is the hair tie material brittle or ductile? Explain your reasoning. [Hint: Compare the stress strain curve with those shown and described in the Qualitative Characterization Methods section at the beginning of the lab.]
14) Is the qualitative stress vs. strain behavior of a hair tie similar to that of a tendon? Explain. [Hint: Do the stress vs. strain curves have all of the same regions? Are the both brittle, both ductile, or is one brittle and one ductile?] Cite any sources that you used to learn about the behavior of tendons.
15) How does the elastic modulus of the hair tie compare to the elastic modulus of a tendon? Provide a ratio of the two values. Also properly cite your source for the tendon value.
16) How does the ultimate strength of the hair tie compare to the ultimate strength of a tendon? Provide a ratio of the two values. Also properly cite your source for the tendon value.
17) Overall, do hair-ties makes good models for tendons? Explain.
Further Questions
18) The toe region in tendons is created by uncrimping of the fibers before the fibers actually stretch. This uncrimping provides joint flexibility by allowing tendon the tendon to easily stretch a short distance under small stress (the slope of the toe region is very shallow). If the tendons remained easy to stretch for long distances then joints would be floppy and muscle contractions would just stretch the tendons instead of move our body parts. Instead, once the tendon fibers are uncrimped the fibers themselves begin to stretch and the tendon becomes very stiff (linear region with steep slope corresponding to the elastic modulus of the tendon material). Explain why hair ties are designed to have a toe region and compare the reasons for a toe region in tendons and hair ties. Cite all sources.
You may have noticed in the video that the outer sheathing around the hair tie appeared to tear while the hair tie was still in the toe region. The stress strain curve continued on the same trend, which means that the sheathing was not providing significant resistance stretching compared to the material inside the hair tie.
14) What do you think is the purpose of the sheathing? Explain your reasoning and cite any and all sources used. [Hint: Do tendons also have a sheathing? If so, what is the purpose of the sheathing?]
