36 8.5 Periodic Trends

One of the reasons the periodic table is so useful is because its structure allows us to qualitatively determine how some properties of the elements vary versus their position on the periodic table. The variation of properties versus position on the periodic table is called periodic trends. There is no other tool in science that allows us to judge relative properties of a class of objects like this, which makes the periodic table a very useful tool. Many periodic trends are general. There may be a few points where an opposite trend is seen, but there is an overall trend when considered across a whole row or down a whole column of the periodic table.

Atomic Radii

The atomic radius is an indication of the size of an atom. Although the concept of a definite radius of an atom is a bit fuzzy, atoms behave as if they have a certain radius. Such radii can be estimated from various experimental techniques, such as the x-ray crystallography of crystals.

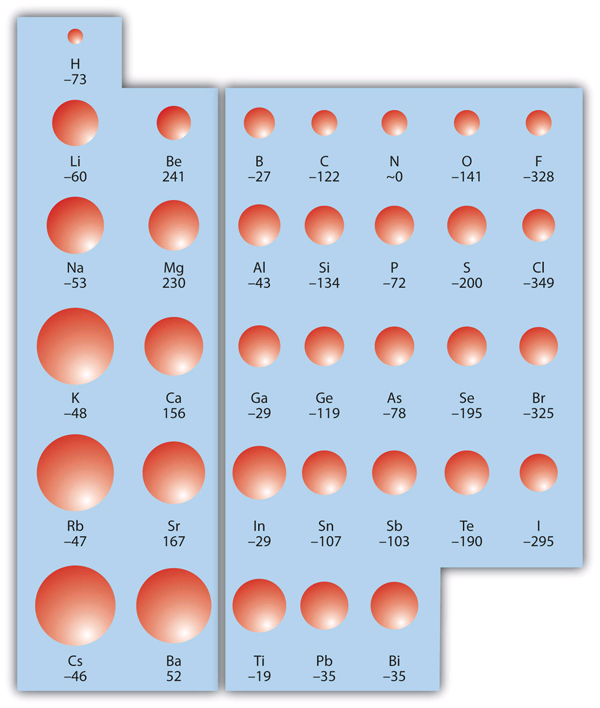
The size of atoms vary and there are two periodic trends.  Atoms get smaller as you go from left to right across a period, and get larger as you go down a group.  Figure 1 “Atomic Radii Trends on the Periodic Table” shows spheres representing the atoms of the s and p blocks from the periodic table to scale, showing the two trends for the atomic radius.

The atomic size is easily explained when we examine how the electron configurations change as we move on the periodic table:

• As you go down a group, the valence electron configuration stays the same, but the number of shells is increasing. Each shell represents distance from the nucleus (as well as energy), thus we expect that ATOMIC SIZE INCREASES as you go down a row on the periodic table.
• As you go from left to right on the periodic table, you are adding electrons to the same shell, but, you are also adding protons (nuclear charge). These protons serve to pull the electrons closer to the nucleus. Thus, we expect that as you go from left to right along each period, ATOMIC SIZE DECREASES.

Ionization Energy

Ionization energy (IE) is the amount of energy required to remove an electron from an atom in the gas phase:

A(g) [latex] \longrightarrow[/latex]A⁺(g) + e⁻             ΔH ≡ IE

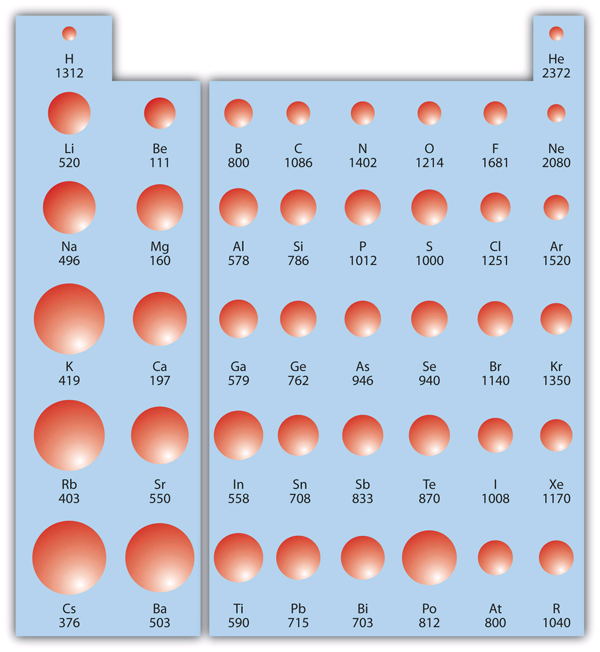
IE is usually expressed in kJ/mol of atoms. It is always positive because the removal of an electron always requires that energy be put in (i.e., it is endothermic). IE also shows periodic trends. As you go down the periodic table, it becomes easier to remove an electron from an atom (i.e., IE decreases) because the valence electron is farther away from the nucleus.  However, as you go across the periodic table and the electrons get drawn closer in, it takes more energy to remove an electron; as a result, IE increases.

Figure 2 “Ionization Energy on the Periodic Table” shows values of IE versus position on the periodic table. Again, the trend isn’t absolute, but the general trends going across and down the periodic table should be obvious.

IE also shows an interesting trend within a given atom. This is because more than one IE can be defined by removing successive electrons (if the atom has them to begin with):

A(g) [latex]\longrightarrow[/latex] A⁺(g) + e⁻ IE₁
A⁺(g) [latex]\longrightarrow[/latex] A²⁺(g) + e⁻ IE₂
A²⁺(g) [latex]\longrightarrow[/latex] A³⁺(g) + e⁻ IE₃

and so forth.

Each successive IE is larger than the previous because an electron is being removed from an atom with a progressively larger positive charge. However, IE takes a large jump when a successive ionization goes down into a new shell. For example, the following are the first three IEs for Mg, whose electron configuration is 1s²2s²2p⁶3s²:

Mg(g) [latex]\longrightarrow[/latex] Mg⁺(g) + e⁻ IE₁ = 738 kJ/mol
Mg⁺(g) [latex]\longrightarrow[/latex] Mg²⁺(g) + e⁻ IE₂ = 1,450 kJ/mol
Mg²⁺(g) [latex]\longrightarrow[/latex] Mg³⁺(g) + e⁻ IE₃ = 7,734 kJ/mol

The second IE is twice the first, which is not a surprise: the first IE involves removing an electron from a neutral atom, while the second one involves removing an electron from a positive ion. The third IE, however, is over five times the previous one. It suggests that there is more involved than simply overcoming a larger ionic charge. Why is it so much larger? Because the first two electrons are removed from the 3s subshell, but the third electron has to be removed from the n = 2 shell, specifically, the 2p subshell, which is lower in energy than the n = 3 shell.  It is evidence like this that demonstrate that electrons are organized in atoms in groups (shells and subshells).

Electron Affinity

The opposite of IE is described by electron affinity (EA), which is the energy change when a gas-phase atom accepts an electron:

A(g) + e⁻[latex]\longrightarrow[/latex] A⁻(g)               ΔH ≡ EA

Electron affinity is also usually expressed in kJ/mol.

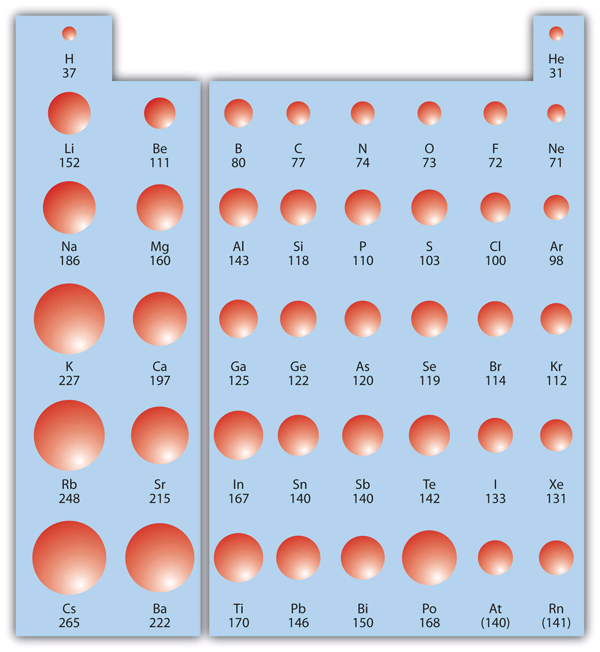
Electron affinity also demonstrates some periodic trends, although they are less obvious than the other periodic trends discussed previously. Figure 3 “Electron Affinity on the Periodic Table” shows EA values versus position on the periodic table for the s– and p-block elements. The trend isn’t absolute, especially considering the large positive EA values for the second column.

• Electron affinity generally increases in magnitude as we move to the right across a period (row) in the periodic table (across a period).
• There is not a definitive trend as you go down a group (column) on the periodic table; sometimes electron affinity increases, sometimes it decreases.