6 2.1 Atomic Theory
Learning Objectives
By the end of this section, you will be able to:
- State the postulates of Dalton’s atomic theory
- Use postulates of Dalton’s atomic theory to explain the laws of definite and multiple proportions
The core ideas of chemistry are used in many disciplines, ranging from medicine to engineering to forensics to art. Chemical symbols are used to represent atoms and elements. Chemical formulas depict molecules as well as the composition of compounds. Chemical equations provide information about chemical reactions.
The most foundational chemistry idea of all is atomic theory. As we consider this theory in some detail we will identify the composition and mass of atoms, the variability of the composition of isotopes, ion formation, and chemical compounds held together by ionic and covalent bonding. We will also introduce one of the most powerful tools for organizing chemical knowledge: the periodic table.
Dalton's Atomic Theory
Modern understandings of chemistry can be traced back to John Dalton who, in 1807, first published his hypothesis that the behavior of matter could be explained using an atomic theory. Dalton’s atomic theory states the following:
- Matter is composed of exceedingly small particles called atoms. An atom is the smallest unit of an element that can participate in a chemical change.
- An element consists of only one type of atom, which has a mass that is characteristic of the element and is the same for all atoms of that element (Figure 1). A macroscopic sample of an element contains an incredibly large number of atoms, all of which have identical chemical properties.

Figure 1. A pre-1982 copper penny (left) contains approximately 3 × 1022 copper atoms (several dozen are represented as brown spheres at the right), each of which has the same chemical properties. (credit: modification of work by “slgckgc”/Flickr) - Atoms of one element differ in properties from atoms of all other elements.
- A compound consists of atoms of two or more elements combined in a small, whole-number ratio. In a given compound, the numbers of atoms of each of its elements are always present in the same ratio (Figure 2).

Figure 2. Copper(II) oxide, a powdery, black compound, results from the combination of two types of atoms—copper (brown spheres) and oxygen (red spheres)—in a 1:1 ratio. (credit: modification of work by “Chemicalinterest”/Wikimedia Commons) - Atoms are neither created nor destroyed during a chemical change, but are instead rearranged to yield substances that are different from those present before the change (Figure 3).
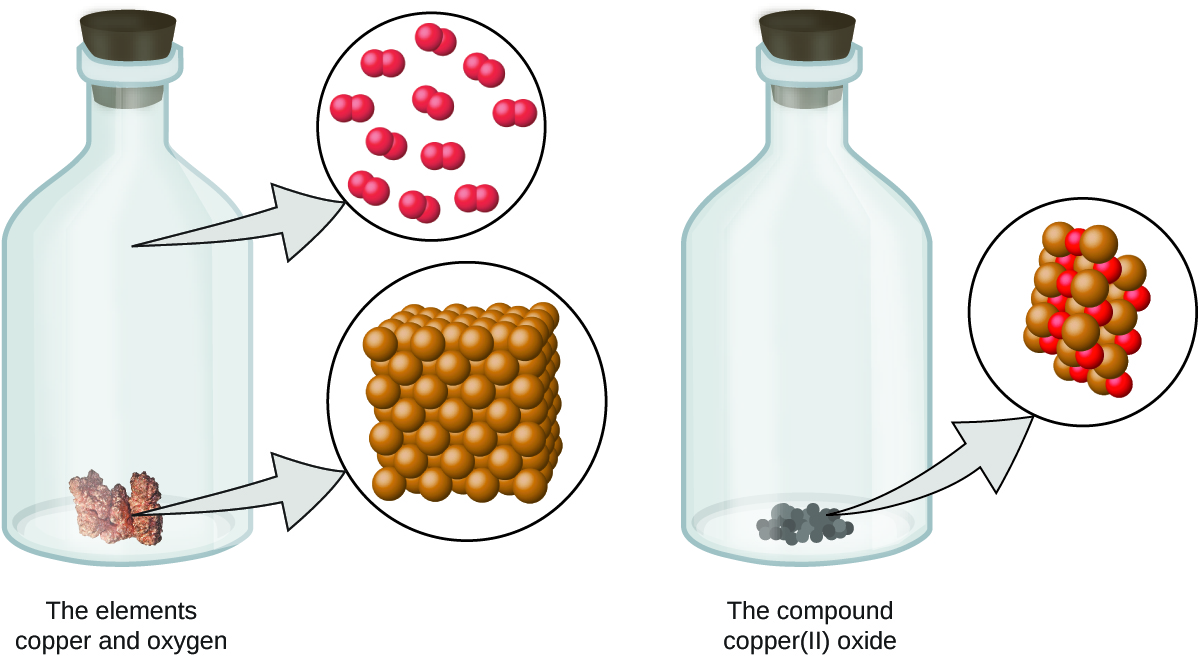
Figure 3. When the elements copper (a shiny, red-brown solid, shown here as brown spheres) and oxygen (a clear and colorless gas, shown here as red spheres) react, their atoms rearrange to form a compound containing copper and oxygen (a powdery, black solid). (credit copper: modification of work by http://images-of-elements.com/copper.php)
Dalton’s atomic theory provides a microscopic explanation of the many macroscopic properties of matter. For example, if an element such as copper consists of only one kind of atom, then it cannot be broken down into simpler substances, that is, into substances composed of fewer types of atoms. And if atoms are neither created nor destroyed during a chemical change, then the total mass of matter present when matter changes from one type to another will remain constant (the law of conservation of matter).
Many of Dalton’s hypotheses about the microscopic features of matter are still valid in modern atomic theory. The shortcomings of his model, however are that it does not account for WHY elements combine as they do and does not explain the observed electrical charge of particles. More discoveries have grown out from, and improved upon his model.
Example 1
In the following drawing, the green spheres represent atoms of a certain element. The purple spheres represent atoms of another element. If the spheres touch, they are part of a single unit of a compound. Does the following chemical change represented by these symbols violate any of the ideas of Dalton’s atomic theory? If so, which one?

Solution
The starting materials consist of two green spheres and two purple spheres. The products consist of only one green sphere and one purple sphere. This violates Dalton’s postulate that atoms are neither created nor destroyed during a chemical change, but are merely redistributed. (In this case, atoms appear to have been destroyed.)
Test Yourself
In the following drawing, the green spheres represent atoms of a certain element. The purple spheres represent atoms of another element. If the spheres touch, they are part of a single unit of a compound. Does the following chemical change represented by these symbols violate any of the ideas of Dalton’s atomic theory? If so, which one?

Answer
The starting materials consist of four green spheres and two purple spheres. The products consist of four green spheres and two purple spheres. This does not violate any of Dalton’s postulates: Atoms are neither created nor destroyed, but are redistributed in small, whole-number ratios.
The Laws of Constant Composition and Multiple Proportions
Dalton knew of the experiments of French chemist Joseph Proust, who demonstrated that all samples of a pure compound contain the same elements in the same proportion by mass. This statement is known as the law of constant composition. The suggestion that the numbers of atoms of the elements in a given compound always exist in the same ratio is consistent with these observations. For example, when different samples of isooctane (a component of gasoline and one of the standards used in the octane rating system) are analyzed, they are found to have a carbon-to-hydrogen mass ratio of 5.33:1, as shown in Table 1.
| Sample | Carbon | Hydrogen | Mass Ratio |
|---|---|---|---|
| A | 14.82 g | 2.78 g | [latex]\frac{14.82 \text{g carbon}}{2.78 \text{g hydrogen}} = \frac{5.33 \text{g carbon}}{1.00 \text{g hydrogen}}[/latex] |
| B | 22.33 g | 4.19 g | [latex]\frac{22.33 \text{g carbon}}{4.19 \text{g hydrogen}} = \frac{5.33 \text{g carbon}}{1.00 \text{g hydrogen}}[/latex] |
| C | 19.40 g | 3.64 g | [latex]\frac{19.40 \text{g carbon}}{3.64 \text{g hydrogen}} = \frac{5.33 \text{g carbon}}{1.00 \text{g hydrogen}}[/latex] |
| Table 1. Constant Composition of Isooctane | |||
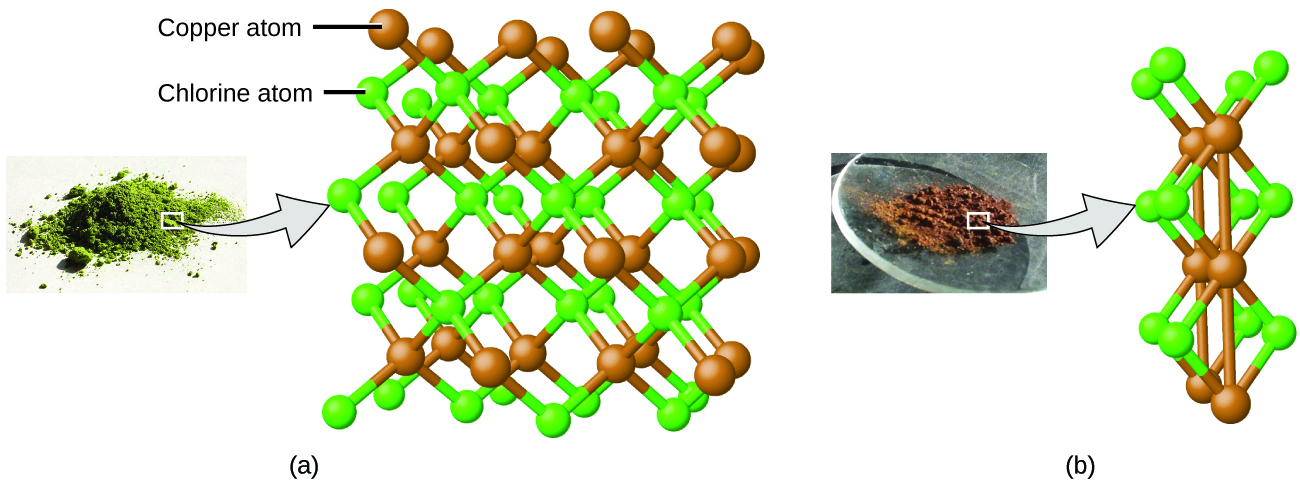
Dalton also used data from Proust, as well as results from his own experiments, to formulate another interesting law. The law of multiple proportions states that when two elements react to form more than one compound, a fixed mass of one element will react with masses of the other element in a ratio of small, whole numbers. For example, copper and chlorine can form a green, crystalline solid with a mass ratio of 0.558 g chlorine to 1.00 g copper, as well as a brown crystalline solid with a mass ratio of 1.116 g chlorine to 1.00 g copper. These ratios by themselves may not seem particularly interesting or informative; however, if we take a ratio of these ratios, we obtain a useful and possibly surprising result: a small, whole-number ratio.
This 2-to-1 ratio means that the brown compound has twice the amount of chlorine per amount of copper as the green compound. This can be explained by atomic theory if the copper-to-chlorine ratio in the brown compound is 1 copper atom to 2 chlorine atoms, and the ratio in the green compound is 1 copper atom to 1 chlorine atom. The ratio of chlorine atoms (and thus the ratio of their masses) is therefore 2 to 1 (Figure 4).
Example 2
A sample of compound A (a clear, colorless gas) is analyzed and found to contain 4.27 g carbon and 5.69 g oxygen. A sample of compound B (also a clear, colorless gas) is analyzed and found to contain 5.19 g carbon and 13.84 g oxygen. Are these data an example of the law of definite proportions, the law of multiple proportions, or neither? What do these data tell you about substances A and B?
Solution
In compound A, the mass ratio of carbon to oxygen is:
In compound B, the mass ratio of carbon to oxygen is:
The ratio of these ratios is:
This supports the law of multiple proportions. This means that A and B are different compounds, with A having one-half as much oxygen per amount of carbon as B. A possible pair of compounds that would fit this relationship would be A = CO and B = CO2.
Test Yourself
A sample of compound X (a clear, colorless, combustible liquid with a noticeable odor) is analyzed and found to contain 14.13 g carbon and 2.96 g hydrogen. A sample of compound Y (a clear, colorless, combustible liquid with a noticeable odor that is slightly different from X’s odor) is analyzed and found to contain 19.91 g carbon and 3.34 g hydrogen. Are these data an example of the law of definite proportions, the law of multiple proportions, or neither? What do these data tell you about substances X and Y?
Answers
In compound X, the mass ratio of carbon to hydrogen is [latex]\frac{14.13 \text{g C}}{2.96 \text{g H}}[/latex] . In compound Y, the mass ratio of carbon to oxygen is [latex]\frac{19.91 \text{g C}}{3.34 \text{g H}}[/latex] . The ratio of these ratios is [latex]\frac{\frac{14.13 \text{g C}}{2.96 \text{g H}}}{\frac{19.91 \text{g C}}{3.34 \text{g H}}} = \frac{4.77 \text{g C/g H}}{5.96 \text{g C/g H}} = 0.800 = \frac{4}{5}[/latex] . This small, whole-number ratio supports the law of multiple proportions. This means that X and Y are different compounds.
Key Concepts and Summary
Dalton postulated that each element has a characteristic type of atom that differs in properties from atoms of all other elements, and that atoms of different elements can combine in fixed, small, whole-number ratios to form compounds. Samples of a particular compound all have the same elemental proportions by mass. When two elements form different compounds, a given mass of one element will combine with masses of the other element in a small, whole-number ratio. During any chemical change, atoms are neither created nor destroyed.
Review-Reflect, Extend
Review-Reflect
1. In the following drawing, the green spheres represent atoms of a certain element. The purple spheres represent atoms of another element. If the spheres of different elements touch, they are part of a single unit of a compound. The following chemical change represented by these spheres may violate one of the ideas of Dalton’s atomic theory. Which one?
2. Which postulate of Dalton’s theory is consistent with the following observation concerning the weights of reactants and products? When 100 grams of solid calcium carbonate is heated, 44 grams of carbon dioxide and 56 grams of calcium oxide are produced.
Do these data provide example(s) of the law of definite proportions, the law of multiple proportions, neither, or both? What do these data tell you about compounds X, Y, and Z?
Extend
- Building blocks such as Duplo® can be used as a rough model for the formation of compounds from atoms of various elements. Using this idea, come up with a scheme for representing the following compounds, with atoms of various elements keyed to a particular type of block:
H2O, representing water with 2 hydrogen atoms and one oxygen atom
CO2, carbon dioxide, with one carbon atom and two oxygen atoms
C3H8, propane, with 3 carbon atoms and 8 hydrogen atoms
Answers to Review-Refresh
1. The starting materials consist of one green sphere and two purple spheres. The products consist of two green spheres and two purple spheres. This violates Dalton’s postulate that that atoms are not created during a chemical change, but are merely redistributed.
2. The law of conservation of matter - the total mass of matter present when matter changes from one type to another remains constant.
3. This statement violates Dalton’s fourth postulate: In a given compound, the numbers of atoms of each type (and thus also the percentage) always have the same ratio.
4. Samples X and Z provide an example of the law of definite proportions (law of constant composition) for both samples are found to have a carbon-to-hydrogen mass ratio of 12:1.
Samples X and Y provide an example of the law of multiple proportions,
since in sample X, the mass ratio of carbon to hydrogen is:
and in sample Y, the mass ratio of carbon to hydrogen is:
The ratio of these ratios is:
This supports the law of multiple proportions. This means that sample X and Y are different compounds, with X having one-half as much hydrogen per amount of carbon as Y.
Samples Z and Y also provide an example of the law of multiple proportions,
since in sample Z, the mass ratio of carbon to hydrogen is:
and in sample Y, the mass ratio of carbon to hydrogen is:
The ratio of these ratios is:
This supports the law of multiple proportions. This means that sample Z and Y are different compounds, with Z having one-half as much hydrogen per amount of carbon as Y.
Note: Samples X and Z may be the same compound or they may be different (isomers - a topic to be discussed later).
Glossary
Dalton’s atomic theory: set of postulates that established the fundamental properties of atoms
law of conservation of matter: the total mass of matter present when matter changes from one type to another remains constant.
law of constant composition: (also, law of definite proportions) all samples of a pure compound contain the same elements in the same proportions by mass
law of definite proportions: (also, law of constant composition) all samples of a pure compound contain the same elements in the same proportions by mass
law of multiple proportions: when two elements react to form more than one compound, a fixed mass of one element will react with masses of the other element in a ratio of small whole numbers

