Learning Objectives
- Analyze arguments against economic approaches to decision-making
- Interpret a tradeoff diagram
- Contrast normative statements and positive statements
It is one thing to understand the economic approach to decision-making and another thing to feel comfortable applying it. The sources of discomfort typically fall into two categories: that people do not act in the way that fits the economic way of thinking, and that even if people did act that way, they should try not to. Let’s consider these arguments in turn.
First Objection: People, Firms, and Society Do Not Act Like This
The economic approach to decision-making seems to require more information than most individuals possess and more careful decision-making than most individuals actually display. After all, do you or any of your friends draw a budget constraint and mutter to yourself about maximizing utility before you head to the shopping mall? Do members of the U.S. Congress contemplate production possibilities frontiers before they vote on the annual budget? The messy ways in which people and societies operate somehow doesn’t look much like neat budget constraints or smoothly curving production possibilities frontiers.
However, the economics approach can be a useful way to analyze and understand the tradeoffs of economic decisions even so. To appreciate this point, imagine for a moment that you are playing basketball, dribbling to the right, and throwing a bounce-pass to the left to a teammate who is running toward the basket. A physicist or engineer could work out the correct speed and trajectory for the pass, given the different movements involved and the weight and bounciness of the ball. But when you are playing basketball, you do not perform any of these calculations. You just pass the ball, and if you are a good player, you will do so with high accuracy.
Someone might argue: “The scientist’s formula of the bounce-pass requires a far greater knowledge of physics and far more specific information about speeds of movement and weights than the basketball player actually has, so it must be an unrealistic description of how basketball passes are actually made.” This reaction would be wrongheaded. The fact that a good player can throw the ball accurately because of practice and skill, without making a physics calculation, does not mean that the physics calculation is wrong.
Similarly, from an economic point of view, someone who goes shopping for groceries every week has a great deal of practice with how to purchase the combination of goods that will provide that person with utility, even if the shopper does not phrase decisions in terms of a budget constraint. Government institutions may work imperfectly and slowly, but in general, a democratic form of government feels pressure from voters and social institutions to make the choices that are most widely preferred by people in that society. So, when thinking about the economic actions of groups of people, firms, and society, it is reasonable, as a first approximation, to analyze them with the tools of economic analysis. For more on this, read about behavioral economics in the chapter on Consumer Choices.
Second Objection: People, Firms, and Society Should Not Act This Way
The economics approach portrays people as self-interested. For some critics of this approach, even if self-interest is an accurate description of how people behave, these behaviors are not moral. Instead, the critics argue that people should be taught to care more deeply about others. Economists offer several answers to these concerns.
First, economics is not a form of moral instruction. Rather, it seeks to describe economic behavior as it actually exists. Philosophers draw a distinction between positive statements, which describe the world as it is, and normative statements, which describe how the world should be. For example, an economist could analyze a proposed subway system in a certain city. If the expected benefits exceed the costs, he concludes that the project is worth doing—an example of positive analysis. Another economist argues for extended unemployment compensation during the Great Depression because a rich country like the United States should take care of its less fortunate citizens—an example of normative analysis.
Even if the line between positive and normative statements is not always crystal clear, economic analysis does try to remain rooted in the study of the actual people who inhabit the actual economy. Fortunately however, the assumption that individuals are purely self-interested is a simplification about human nature. In fact, we need to look no further than to Adam Smith, the very father of modern economics to find evidence of this. The opening sentence of his book, The Theory of Moral Sentiments, puts it very clearly: “How selfish soever man may be supposed, there are evidently some principles in his nature, which interest him in the fortune of others, and render their happiness necessary to him, though he derives nothing from it except the pleasure of seeing it.” Clearly, individuals are both self-interested and altruistic.
Second, self-interested behavior and profit-seeking can be labeled with other names, such as personal choice and freedom. The ability to make personal choices about buying, working, and saving is an important personal freedom. Some people may choose high-pressure, high-paying jobs so that they can earn and spend a lot of money on themselves. Others may earn a lot of money and give it to charity or spend it on their friends and family. Others may devote themselves to a career that can require a great deal of time, energy, and expertise but does not offer high financial rewards, like being an elementary school teacher or a social worker. Still others may choose a job that does not take lots of their time or provide a high level of income, but still leaves time for family, friends, and contemplation. Some people may prefer to work for a large company; others might want to start their own business. People’s freedom to make their own economic choices has a moral value worth respecting.
Is a diagram by any other name the same?
When you study economics, you may feel buried under an avalanche of diagrams: diagrams in the text, diagrams in the lectures, diagrams in the problems, and diagrams on exams. Your goal should be to recognize the common underlying logic and pattern of the diagrams, not to memorize each of the individual diagrams.
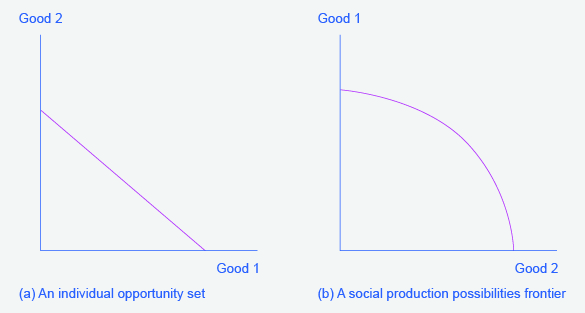
This chapter uses only one basic diagram, although it is presented with different sets of labels. The consumption budget constraint and the production possibilities frontier for society, as a whole, are the same basic diagram. Figure 1 shows an individual budget constraint and a production possibilities frontier for two goods, Good 1 and Good 2. The tradeoff diagram always illustrates three basic themes: scarcity, tradeoffs, and economic efficiency.
The first theme is scarcity. It is not feasible to have unlimited amounts of both goods. But even if the budget constraint or a PPF shifts, scarcity remains—just at a different level. The second theme is tradeoffs. As depicted in the budget constraint or the production possibilities frontier, it is necessary to give up some of one good to gain more of the other good. The details of this tradeoff vary. In a budget constraint, the tradeoff is determined by the relative prices of the goods: that is, the relative price of two goods in the consumption choice budget constraint. These tradeoffs appear as a straight line. However, the tradeoffs in many production possibilities frontiers are represented by a curved line because the law of diminishing returns holds that as resources are added to an area, the marginal gains tend to diminish. Regardless of the specific shape, tradeoffs remain.
The third theme is economic efficiency, or getting the most benefit from scarce resources. All choices on the production possibilities frontier show productive efficiency because in such cases, there is no way to increase the quantity of one good without decreasing the quantity of the other. Similarly, when an individual makes a choice along a budget constraint, there is no way to increase the quantity of one good without decreasing the quantity of the other. The choice on a production possibilities set that is socially preferred, or the choice on an individual’s budget constraint that is personally preferred, will display allocative efficiency.
The basic budget constraint/production possibilities frontier diagram will recur throughout this book. Some examples include using these tradeoff diagrams to analyze trade, labor supply versus leisure, saving versus consumption, environmental protection and economic output, equality of incomes and economic output, and the macroeconomic tradeoff between consumption and investment. Do not be confused by the different labels. The budget constraint/production possibilities frontier diagram is always just a tool for thinking carefully about scarcity, tradeoffs, and efficiency in a particular situation.
Third, self-interested behavior can lead to positive social results. For example, when people work hard to make a living, they create economic output. Consumers who are looking for the best deals will encourage businesses to offer goods and services that meet their needs. Adam Smith, writing in The Wealth of Nations, christened this property the invisible hand. In describing how consumers and producers interact in a market economy, Smith wrote:
Every individual…generally, indeed, neither intends to promote the public interest, nor knows how much he is promoting it. By preferring the support of domestic to that of foreign industry, he intends only his own security; and by directing that industry in such a manner as its produce may be of the greatest value, he intends only his own gain. And he is in this, as in many other cases, led by an invisible hand to promote an end which was no part of his intention…By pursuing his own interest he frequently promotes that of the society more effectually than when he really intends to promote it.
The metaphor of the invisible hand suggests the remarkable possibility that broader social good can emerge from selfish individual actions.
Fourth, even people who focus on their own self-interest in the economic part of their life often set aside their own narrow self-interest in other parts of life. For example, you might focus on your own self-interest when asking your employer for a raise or negotiating to buy a car. But then you might turn around and focus on other people when you volunteer to read stories at the local library, help a friend move to a new apartment, or donate money to a charity. Self-interest is a reasonable starting point for analyzing many economic decisions, without needing to imply that people never do anything that is not in their own immediate self-interest.
Choices … To What Degree?
What have we learned? We know that scarcity impacts all the choices we make. So, an economist might argue that people do not go on to get bachelor’s degrees or master’s degrees because they do not have the resources to make those choices or because their incomes are too low and/or the price of these degrees is too high. A bachelor’s degree or a master’s degree may not be available in their opportunity set.
The price of these degrees may be too high not only because the actual price, college tuition (and perhaps room and board), is too high. An economist might also say that for many people, the full opportunity cost of a bachelor’s degree or a master’s degree is too high. For these people, they are unwilling or unable to make the tradeoff of giving up years of working, and earning an income, to earn a degree.
Finally, the statistics introduced at the start of the chapter reveal information about intertemporal choices. An economist might say that people choose not to get a college degree because they may have to borrow money to go to college, and the interest they have to pay on that loan in the future will affect their decisions today. Also, it could be that some people have a preference for current consumption over future consumption, so they choose to work now at a lower salary and consume now, rather than putting that consumption off until after they graduate college.
Key Concepts and Summary
The economic way of thinking provides a useful approach to understanding human behavior. Economists make the careful distinction between positive statements, which describe the world as it is, and normative statements, which describe how the world should be. Even when economics analyzes the gains and losses from various events or policies, and thus draws normative conclusions about how the world should be, the analysis of economics is rooted in a positive analysis of how people, firms, and governments actually behave, not how they should behave.
Self-Check Questions
- Individuals may not act in the rational, calculating way described by the economic model of decision making, measuring utility and costs at the margin, but can you make a case that they behave approximately that way?
- Would an op-ed piece in a newspaper urging the adoption of a particular economic policy be considered a positive or normative statement?
- Would a research study on the effects of soft drink consumption on children’s cognitive development be considered a positive or normative statement?
Review Questions
- What is the difference between a positive and a normative statement?
- Is the economic model of decision-making intended as a literal description of how individuals, firms, and the governments actually make decisions?
- What are four responses to the claim that people should not behave in the way described in this chapter?
Critical Thinking Questions
- What assumptions about the economy must be true for the invisible hand to work? To what extent are those assumptions valid in the real world?
- Do economists have any particular expertise at making normative arguments? In other words, they have expertise at making positive statements (i.e., what will happen) about some economic policy, for example, but do they have special expertise to judge whether or not the policy should be undertaken?
References
Smith, Adam. “Of Restraints upon the Importation from Foreign Countries.” In The Wealth of Nations. London: Methuen & Co., 1904, first pub 1776), I.V. 2.9.
Smith, Adam. “Of the Propriety of Action.” In The Theory of Moral Sentiments. London: A. Millar, 1759, 1.
Glossary
- invisible hand
- idea that self-interested behavior by individuals can lead to positive social outcomes
- normative statement
- statement which describes how the world should be
- positive statement
- statement which describes the world as it is
Solutions
Answers to Self-Check Questions
- When individuals compare cost per unit in the grocery store, or characteristics of one product versus another, they are behaving approximately like the model describes.
- Since an op-ed makes a case for what should be, it is considered normative.
- Assuming that the study is not taking an explicit position about whether soft drink consumption is good or bad, but just reporting the science, it would be considered positive.

