3.2 Biogeochemical Cycles
Energy flows directionally through ecosystems, entering as sunlight (or inorganic molecules for chemoautotrophs) and leaving as heat during energy transformation between trophic levels. Rather than flowing through an ecosystem, the matter that makes up organisms is conserved and recycled. The six most common elements associated with organic molecules—carbon, nitrogen, hydrogen, oxygen, phosphorus, and sulfur—take a variety of chemical forms and may exist for long periods in the atmosphere, on land, in water, or beneath Earth’s surface. Geologic processes, such as weathering, erosion, water drainage, and the subduction of the continental plates, all play a role in the cycling of elements on Earth. Because geology and chemistry have major roles in the study of these processes, the recycling of inorganic matter between living organisms and their nonliving environment are called biogeochemical cycles.
The six aforementioned elements are used by organisms in a variety of ways. Hydrogen and oxygen are found in water and organic molecules, both of which are essential to life. Carbon is found in all organic molecules, whereas nitrogen is an important component of nucleic acids and proteins. Phosphorus is used to make nucleic acids and the phospholipids that comprise biological membranes. Lastly, sulfur is critical to the three-dimensional shape of proteins.
The cycling of these elements is interconnected. For example, the movement of water is critical for the leaching of sulfur and phosphorus into rivers, lakes, and oceans. Minerals cycle through the biosphere between the biotic and abiotic components and from one organism to another.
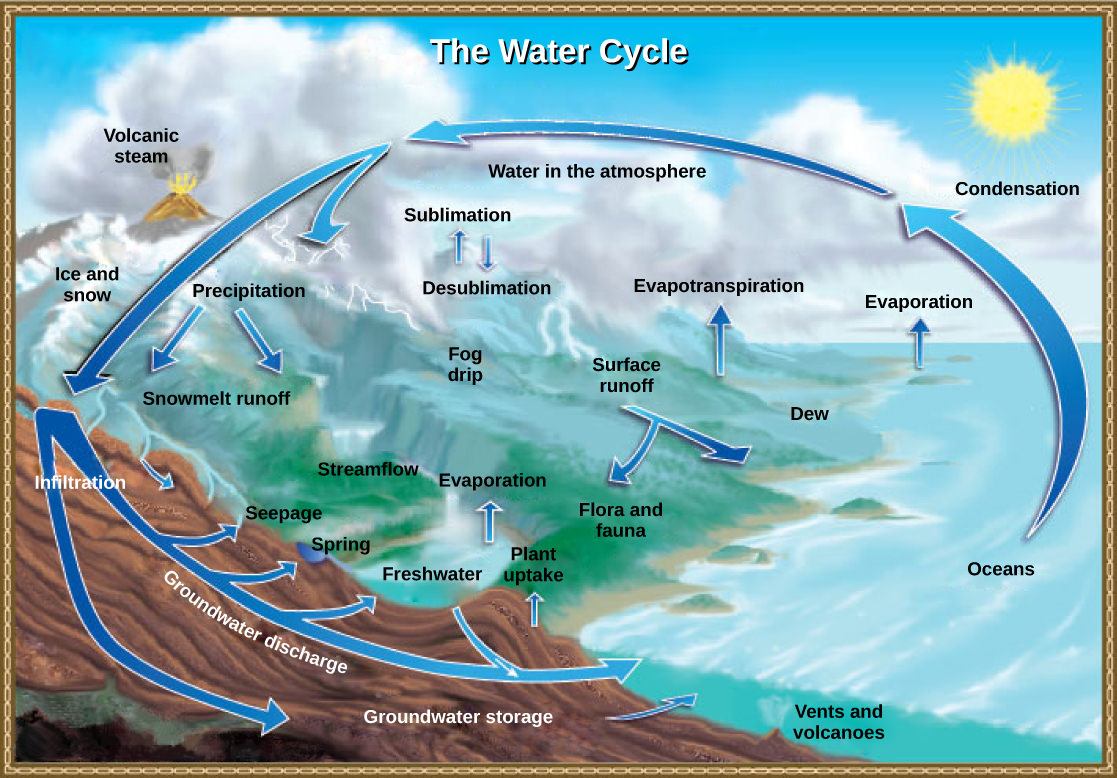
The Water Cycle
The hydrosphere is the area of Earth where water movement and storage occurs: as liquid water on the surface (rivers, lakes, oceans) and beneath the surface (groundwater) or ice, (polar ice caps and glaciers), and as water vapor in the atmosphere.The human body is about 60 percent water and human cells are more than 70 percent water. Of the stores of water on Earth, 97.5 percent is salt water (see Figure 1 below). Of the remaining water, more than 99 percent is groundwater or ice. Thus, less than one percent of freshwater is present in lakes and rivers. Many organisms are dependent on this small percentage, a lack of which can have negative effects on ecosystems. Humans, of course, have developed technologies to increase water availability, such as digging wells to harvest groundwater, storing rainwater, and using desalination to obtain drinkable water from the ocean. Although this pursuit of drinkable water has been ongoing throughout human history, the supply of fresh water continues to be a major issue in modern times.
The various processes that occur during the cycling of water are illustrated in Figure 2 below. The processes include the following:

- evaporation and sublimation
- condensation and precipitation
- subsurface water flow
- surface runoff and snowmelt
- streamflow
The water cycle is driven by the Sun’s energy as it warms the oceans and other surface waters. This leads to evaporation (liquid water to water vapor) of liquid surface water and sublimation (ice to water vapor) of frozen water, thus moving large amounts of water into the atmosphere as water vapor. Over time, this water vapor condenses into clouds as liquid or frozen droplets and eventually leads to precipitation (rain, snow, hail), which returns water to Earth’s surface. Rain reaching Earth’s surface may evaporate again, flow over the surface, or percolate into the ground. Most easily observed is surface runoff: the flow of freshwater over land either from rain or melting ice. Runoff can make its way through streams and lakes to the oceans.
In most natural terrestrial environments rain encounters vegetation before it reaches the soil surface. A significant percentage of water evaporates immediately from the surfaces of plants. What is left reaches the soil and begins to move down. Surface runoff will occur only if the soil becomes saturated with water in a heavy rainfall. Water in the soil can be taken up by plant roots. The plant will use some of this water for its own metabolism and some of that will find its way into animals that eat the plants, but much of it will be lost back to the atmosphere through a process known as transpiration: water enters the vascular system of plants through the roots and evaporates, or transpires, through the stomata (small microscope openings) of the leaves. Ecologists combine transpiration and evaporation into a single term that describes water returned to the atmosphere: evapotranspiration. Water in the soil that is not taken up by a plant and that does not evaporate is able to percolate into the subsoil and bedrock where it forms groundwater.
Groundwater is a significant, subsurface reservoir of fresh water. It exists in the pores between particles in dirt, sand, and gravel or in the fissures in rocks. Groundwater can flow slowly through these pores and fissures and eventually finds its way to a stream or lake where it becomes part of the surface water again. Many streams flow not because they are replenished from rainwater directly but because they receive a constant inflow from the groundwater below. Some groundwater is found very deep in the bedrock and can persist there for millennia. Most groundwater reservoirs, or aquifers, are the source of drinking or irrigation water drawn up through wells. In many cases these aquifers are being depleted faster than they are being replenished by water percolating down from above.
Rain and surface runoff are major ways in which minerals, including phosphorus and sulfur, are cycled from land to water. The environmental effects of runoff will be discussed later as these cycles are described.
The Carbon Cycle
Carbon is the second most abundant element in organisms, by mass. Carbon is present in all organic molecules (and some molecules that are not organic such as CO2), and its role in the structure of biomolecules is of primary importance. Carbon compounds contain energy, and many of these compounds from dead plants and algae have fossilized over millions of years and are known as fossil fuels. Since the 1800s, the use of fossil fuels has accelerated. Since the beginning of the Industrial Revolution the demand for Earth’s limited fossil fuel supplies has risen, causing the amount of carbon dioxide in our atmosphere to drastically increase. This increase in carbon dioxide is associated with climate change and is a major environmental concern worldwide.
The carbon cycle is most easily studied as two interconnected subcycles: one dealing with rapid carbon exchange among living organisms and the other dealing with the long-term cycling of carbon through geologic processes. The entire carbon cycle is shown in Figure 3 below.
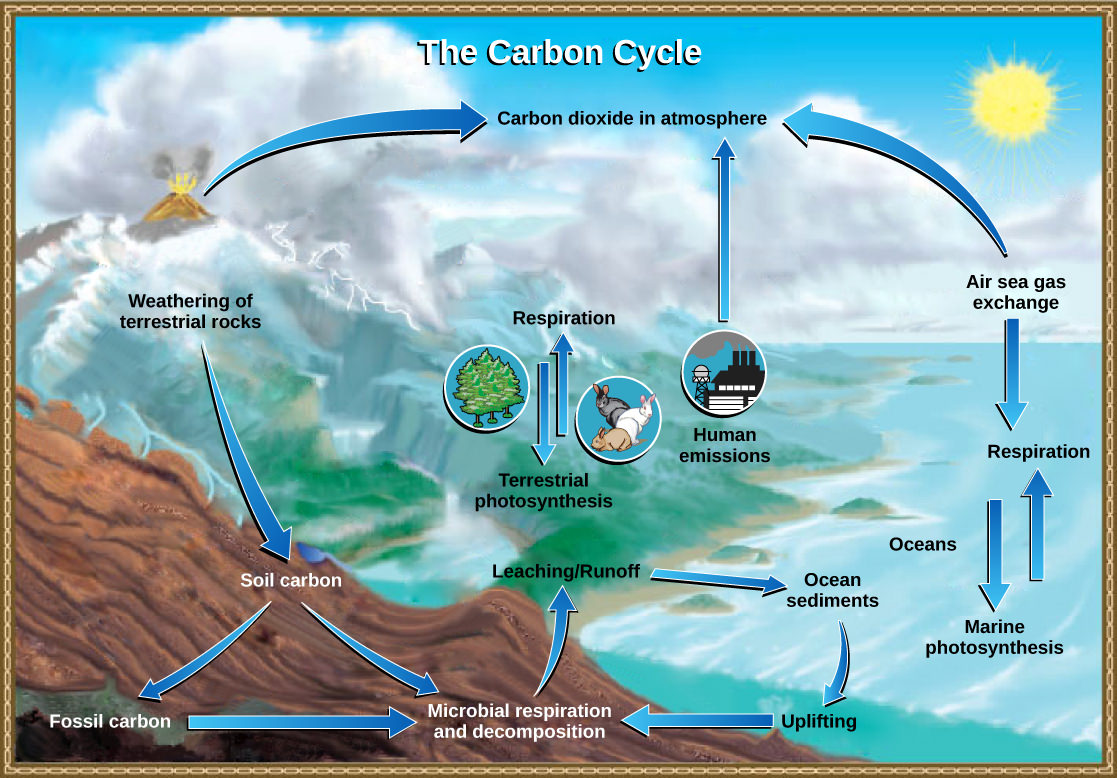
The Biological Carbon Cycle
Organisms are connected in many ways, even among different ecosystems. A good example of this connection is the exchange of carbon between heterotrophs and autotrophs by way of atmospheric carbon dioxide. Carbon dioxide (CO2) is the basic building block that autotrophs use to build high-energy compounds such as glucose. The energy harnessed from the Sun is used by these organisms to form the covalent bonds that link carbon atoms together. These chemical bonds store this energy for later use in the process of respiration. Most terrestrial autotrophs obtain their carbon dioxide directly from the atmosphere, while marine autotrophs acquire it in the dissolved form (bicarbonate, HCO3–).
Carbon is passed from producers to higher trophic levels through consumption. For example, when a cow (primary consumer) eats grass (producer), it obtains some of the organic molecules originally made by the plant’s photosynthesis. Those organic compounds can then be passed to higher trophic levels, such as humans, when we eat the cow. At each level, however, organisms are performing respiration, a process in which organic molecules are broken down to release energy. As these organic molecules are broken down, carbon is removed from food molecules to form CO2, a gas that enters the atmosphere. Thus, CO2 is a byproduct of respiration. Recall that CO2 is consumed by producers during photosynthesis to make organic molecules. As these molecules are broken down during respiration, the carbon once again enters the atmosphere as CO2. Carbon exchange like this potentially connects all organisms on Earth. Think about this: the carbon in your DNA was once part of plant; millions of years ago perhaps it was part of dinosaur.
The Biogeochemical Carbon Cycle
The movement of carbon through land, water, and air is complex, and, in many cases, it occurs much more slowly than the movement between organisms. Carbon is stored for long periods in what are known as carbon reservoirs, which include the atmosphere, bodies of liquid water (mostly oceans), ocean sediment, soil, rocks (including fossil fuels), and Earth’s interior.
As stated, the atmosphere is a major reservoir of carbon in the form of carbon dioxide that is essential to the process of photosynthesis. The level of carbon dioxide in the atmosphere is greatly influenced by the reservoir of carbon in the oceans. The exchange of carbon between the atmosphere and water reservoirs influences how much carbon is found in each. Carbon dioxide (CO2) from the atmosphere dissolves in water and reacts with water molecules to form ionic compounds. Some of these ions combine with calcium ions in the seawater to form calcium carbonate (CaCO3), a major component of the shells of marine organisms. These organisms eventually die and their shells form sediments on the ocean floor. Over geologic time, the calcium carbonate forms limestone, which comprises the largest carbon reservoir on Earth.
On land, carbon is stored in soil as organic carbon as a result of the decomposition of organisms or from weathering of terrestrial rock and minerals (the world’s soils hold significantly more carbon than the atmosphere, for comparison). Deeper underground are fossil fuels, the anaerobically decomposed remains of plants and algae that lived millions of years ago. Fossil fuels are considered a non-renewable resource because their use far exceeds their rate of formation. A non-renewable resource is either regenerated very slowly or not at all. Another way for carbon to enter the atmosphere is from land (including land beneath the surface of the ocean) by the eruption of volcanoes and other geothermal systems. Carbon sediments from the ocean floor are taken deep within Earth by the process of subduction: the movement of one tectonic plate beneath another. Carbon is released as carbon dioxide when a volcano erupts or from volcanic hydrothermal vents.
The Nitrogen Cycle
Getting nitrogen into living organisms is difficult. Plants and phytoplankton are not equipped to incorporate nitrogen from the atmosphere (where it exists as tightly bonded, triple covalent N2) even though this molecule comprises approximately 78 percent of the atmosphere. Nitrogen enters the living world through free-living and symbiotic bacteria, which incorporate nitrogen into their organic molecules through specialized biochemical processes. Certain species of bacteria are able to perform nitrogen fixation, the process of converting nitrogen gas into ammonia (NH3), which spontaneously becomes ammonium (NH4+). Ammonium is converted by bacteria into nitrites (NO2−) and then nitrates (NO3−). At this point, the nitrogen-containing molecules are used by plants and other producers to make organic molecules such as DNA and proteins. This nitrogen is now available to consumers.
Organic nitrogen is especially important to the study of ecosystem dynamics because many ecosystem processes, such as primary production, are limited by the available supply of nitrogen. As shown in Figure 4 below, the nitrogen that enters living systems is eventually converted from organic nitrogen back into nitrogen gas by bacteria (Figure 4). The process of denitrification is when bacteria convert the nitrates into nitrogen gas, thus allowing it to re-enter the atmosphere.

Human activity can alter the nitrogen cycle by two primary means: the combustion of fossil fuels, which releases different nitrogen oxides, and by the use of artificial fertilizers (which contain nitrogen and phosphorus compounds) in agriculture, which are then washed into lakes, streams, and rivers by surface runoff. Atmospheric nitrogen (other than N2) is associated with several effects on Earth’s ecosystems including the production of acid rain (as nitric acid, HNO3) and greenhouse gas effects (as nitrous oxide, N2O), potentially causing climate change. A major effect from fertilizer runoff is saltwater and freshwater eutrophication, a process whereby nutrient runoff causes the overgrowth of algae, the depletion of oxygen, and death of aquatic fauna.
In marine ecosystems, nitrogen compounds created by bacteria, or through decomposition, collects in ocean floor sediments. It can then be moved to land in geologic time by uplift of Earth’s crust and thereby incorporated into terrestrial rock. Although the movement of nitrogen from rock directly into living systems has been traditionally seen as insignificant compared with nitrogen fixed from the atmosphere, a recent study showed that this process may indeed be significant and should be included in any study of the global nitrogen cycle.
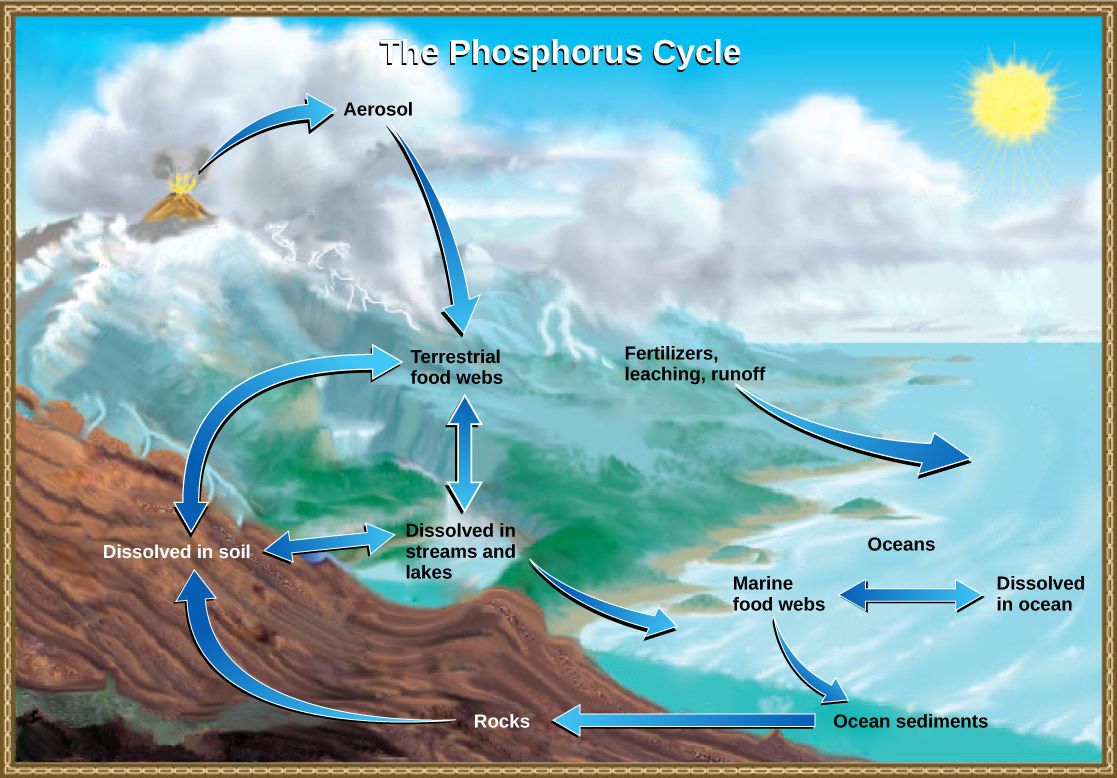
The Phosphorus Cycle
Phosphorus is an essential nutrient for living processes. It is a major component of nucleic acids and phospholipids, and, as calcium phosphate, it makes up the supportive components of our bones. Phosphorus is often the limiting nutrient (necessary for growth) in aquatic, particularly freshwater, ecosystems.
Phosphorus occurs in nature as the phosphate ion (PO43-). In addition to phosphate runoff as a result of human activity, natural surface runoff occurs when it is leached from phosphate-containing rock by weathering, thus sending phosphates into rivers, lakes, and the ocean. This rock has its origins in the ocean. Phosphate-containing ocean sediments form primarily from the bodies of ocean organisms and from their excretions. However, volcanic ash, aerosols, and mineral dust may also be significant phosphate sources. This sediment then is moved to land over geologic time by the uplifting of Earth’s surface. (Figure below)
Phosphorus is also reciprocally exchanged between phosphate dissolved in the ocean and marine organisms. The movement of phosphate from the ocean to the land and through the soil is extremely slow, with the average phosphate ion having an oceanic residence time between 20,000 and 100,000 years.
Excess phosphorus and nitrogen that enter these ecosystems from fertilizer runoff and from sewage cause excessive growth of algae. The subsequent death and decay of these organisms depletes dissolved oxygen, which leads to the death of aquatic organisms such as shellfish and fish. This process is responsible for dead zones in lakes and at the mouths of many major rivers and for massive fish kills, which often occur during the summer months (see Figure 6 below).

A dead zone is an area in lakes and oceans near the mouths of rivers where large areas are periodically depleted of their normal flora and fauna. These zones are caused by eutrophication coupled with other factors including oil spills, dumping toxic chemicals, and other human activities. The number of dead zones has increased for several years, and more than 400 of these zones were present as of 2008. One of the worst dead zones is off the coast of the United States in the Gulf of Mexico: fertilizer runoff from the Mississippi River basin created a dead zone of over 8,463 square miles. Phosphate and nitrate runoff from fertilizers also negatively affect several lake and bay ecosystems including the Chesapeake Bay in the eastern United States.
The Sulfur Cycle
Sulfur is an essential element for the molecules of living things. As part of the amino acid cysteine, it is involved in the formation of proteins. As shown in Figure 7 below, sulfur cycles between the oceans, land, and atmosphere. Atmospheric sulfur is found in the form of sulfur dioxide (SO2), which enters the atmosphere in three ways: first, from the decomposition of organic molecules; second, from volcanic activity and geothermal vents; and, third, from the burning of fossil fuels by humans.
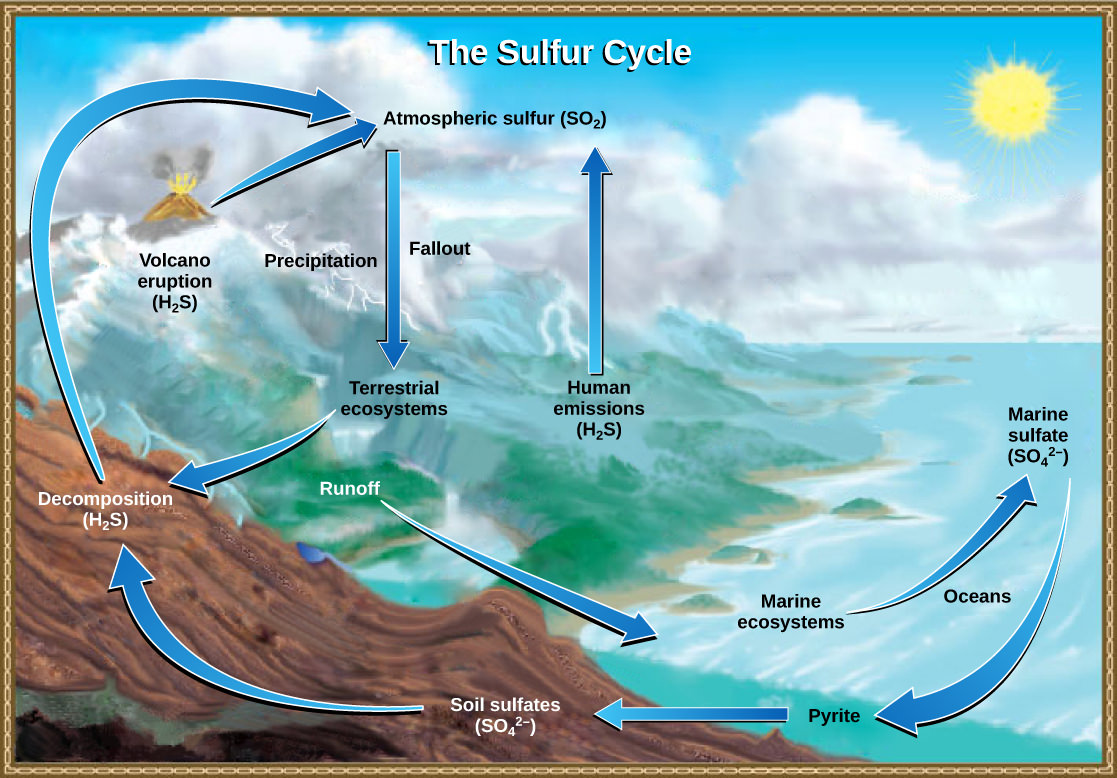
On land, sulfur is deposited in four major ways: precipitation, direct fallout from the atmosphere, rock weathering, and geothermal vents. Atmospheric sulfur is found in the form of sulfur dioxide (SO2), and as rain falls through the atmosphere, sulfur is dissolved in the form of weak sulfuric acid (H2SO4). Sulfur can also fall directly from the atmosphere in a process called fallout. Also, as sulfur-containing rocks weather, sulfur is released into the soil. These rocks originate from ocean sediments that are moved to land by the geologic uplifting of ocean sediments. Terrestrial ecosystems can then make use of these soil sulfates (SO42-), which enter the food web by being taken up by plant roots. When these plants decompose and die, sulfur is released back into the atmosphere as hydrogen sulfide (H2S) gas.
Sulfur enters the ocean in runoff from land, from atmospheric fallout, and from underwater geothermal vents. Some ecosystems rely on chemoautotrophs using sulfur as a biological energy source. This sulfur then supports marine ecosystems in the form of sulfates.
Human activities have played a major role in altering the balance of the global sulfur cycle. The burning of large quantities of fossil fuels, especially from coal, releases larger amounts of hydrogen sulfide gas into the atmosphere. As rain falls through this gas, it creates the phenomenon known as acid rain, which damages the natural environment by lowering the pH of lakes, thus killing many of the resident plants and animals. Acid rain is corrosive rain caused by rainwater falling to the ground through sulfur dioxide gas, turning it into weak sulfuric acid, which causes damage to aquatic ecosystems. Acid rain also affects the man-made environment through the chemical degradation of buildings. For example, many marble monuments, such as the Lincoln Memorial in Washington, DC, have suffered significant damage from acid rain over the years. These examples show the wide-ranging effects of human activities on our environment and the challenges that remain for our future.
Suggested Supplementary Reading
Bruckner, M. 2018. The Gulf of Mexico Dead Zone. [Website] <https://serc.carleton.edu/microbelife/topics/deadzone/index.html>
Attribution
Biogeochemical Cycles by OpenStax is licensed under CC BY 4.0. Modified from the original by Matthew R. Fisher.

