19 Unit 2: CNC Machine Tool Programmable Axes and Position Dimensioning Systems
OBJECTIVE
After completing this unit, you should be able to:
- Understand the cartesian coordinate system.
- Understand the Cartesian coordinates of the plane.
- Understand the Cartesian coordinates of three-dimensional space.
- Understand the four Quadrants.
- Explain the difference between polar and rectangular coordinated.
- Identify the programmable axes on a CNC machining.
THE CARTESIAN COORDINATE SYSTEM
Cartesian coordinates allow one to specify the location of a point in the plane, or in three-dimensional space. The Cartesian coordinates or rectangular coordinates system of a point are a pair of numbers (in two-dimensions) or a triplet of numbers (in three-dimensions) that specified signed distances from the coordinate axis. First we must understand a coordinate system to define our directions and relative position. A system used to define points in space by establishing directions(axis) and a reference position(origin). A coordinate system can be rectangular or polar.
Just as points on the line can be placed in one to one correspondence with the real number line, so points in plane can be placed in one to one correspondence with pairs of real number line by using two coordinate lines. To do this, we construct two perpendicular coordinate line that intersect at their origins; for convenience. Assign a set of equally space graduations to the x and y axes starting at the origin and going in both directions, left and right (x axis) and up and down (y axis) point along each axis may be established. We make one of the number lines vertical with its positive direction upward and negative direction downward. The other number lines horizontal with its positive direction to the right and negative direction to the left. The two number lines are called coordinate axes; the horizontal line is the x axis, the vertical line is the y axis, and the coordinate axes together form the Cartesian coordinate system or a rectangular coordinate system. The point of intersection of the coordinate axes is denoted by O and is the origin of the coordinate system. See Figure 1.
Figure 1
It is basically, Two Real Number Lines Put Together, one going left-right, and the other going up-down. The horizontal line is called x-axis and the vertical line is called y-axis.
The Origin
The point (0,0) is given the special name “The Origin”, and is sometimes given the letter “O”.
Real Number Line
The basis of this system is the real number line marked at equal intervals. The axis is labeled (X, Y or Z). One point on the line is designated as the Origin. Numbers on one side of the line are marked as positive and those to the other side marked negative. See Figure 2.
Figure 2. X-axis number line
Cartesian coordinates of the plane
A plane in which a rectangular coordinate system has been introduced is a coordinate plane or an x-y-plane. We will now show how to establish a one to one correspondence between points in a coordinate plane and pairs of real number. If A is a point in a coordinate plane, then we draw two lines through A, one perpendicular to the x-axis and one perpendicular to the y-axis. If the first line intersects the x-axis at the point with coordinate x and the second line intersects the y-axis at the point with coordinate y, then we associate the pair (x,y) with the A( See Figure 2). The number a is the x-coordinate or abscissa of P and the number b is the y-coordinate or ordinate of p; we say that A is the point with coordinate (x,y) and denote the point by A(x,y). The point (0,0) is given the special name “The Origin”, and is sometimes given the letter “O”.
Abscissa and Ordinate:
The words “Abscissa” and “Ordinate” … they are just the x and y values:
- Abscissa: the horizontal (“x”) value in a pair of coordinates: how far along the point is.
- Ordinate: the vertical (“y”) value in a pair of coordinates: how far up or down the point is.
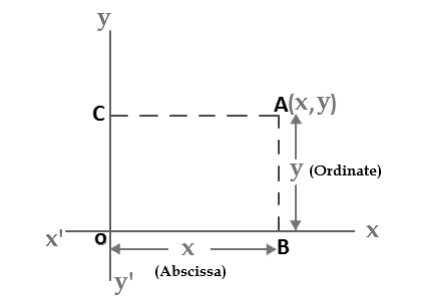
Figure 3
Negative Values of X and Y:
The Real Number Line, you can also have negative values.
Negative: start at zero and head in the opposite direction; See Figure 4
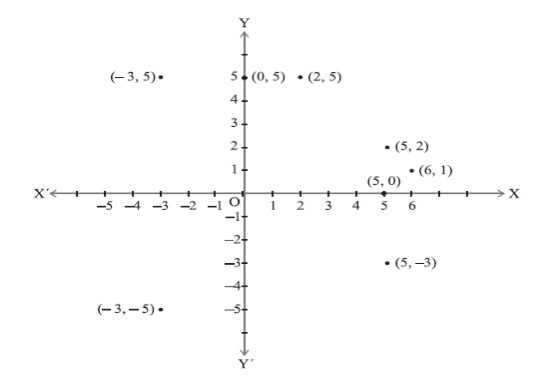
Figure 4
So, for a negative number:
- go left for x
- go down for y
go left along the x axis 3 then go up 5 in the y-axis. (Quadrant II x is negative ,y is positive)
go left along the x axis 3 then go down 5 in the y-axis. (Quadrant III x is negative ,y is negative)

Figure 6
It is basically, a set of two Real Number lines.
Axis: The reference line from which distances are measured.
Example:
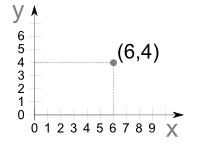
Go along the x direction 6 units then go up 4 units up in the y direction then “plot the dot”.
And you can remember which axis is which by:
The coordinates are always written in a certain order:
- the horizontal distance first,
- then the vertical distance.
Ordered pair:
The numbers are separated by a comma, and parentheses are put around the whole thing like this: (7,4)
Example: (7,4) means 7 units to the right(x-axis), and 4 units up(y-axis)
Cartesian coordinates of three-dimensional space
In three-dimensional space(xyz space), oriented at right angles to the xy-plane. The z axis, passes through the origin of the xy-plane. Coordinates are determined according to the east-west for x-axis north-south for y-axis, and up-down for the z-axis displacements from the origin. The Cartesian coordinate system is based on three mutually perpendicular coordinate axes: the x-axis, the y-axis, and the z-axis, See Figure 6 below. The three axes intersect at the point called the origin. You can imagine the origin being the point where the walls in the corner of a room meet the floor. The x-axis is the horizontal line along which the wall to your left and the floor intersect. The y-axis is the horizontal line along which the wall to your right and the floor intersect. The z-axis is the vertical line along which the walls intersect. The parts of the lines that you see while standing in the room are the positive portion of each of the axes. The negative part of these axes would be the continuations of the lines outside of the room.

Figure 7. 3D Cartesian Coordinate System
Three-dimensional Cartesian coordinate axes. A representation of the three axes of the three-dimensional Cartesian coordinate system. The positive x-axis, positive y-axis, and positive z-axis are the sides labeled by x, y and z. The origin is the intersection of all the axes. The branch of each axis on the opposite side of the origin (the unlabeled side) is the negative part.
When dealing with 3-dimensional motion, is to set up a suitable coordinate system. The most straight-forward type of coordinate system is called a Cartesian system. A Cartesian coordinate system consists of three mutually perpendicular axes, the X, Y, and Z-axes. By convention, the orientation of these axes is such that when the index finger, the middle finger, and the thumb of the right-hand are configured so as to be mutually perpendicular, the index finger, the middle finger, and the thumb can be aligned along the X, Y, and Z-axes, respectively. Such a coordinate system is termed right-handed. See Figure 7. The point of intersection of the three coordinate axes is termed the origin of the coordinate system.
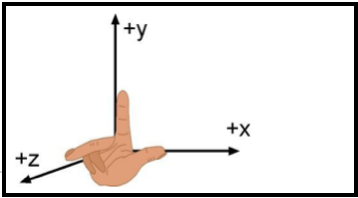
Figure 8. The Right Handed Cartesian System
The Cartesian coordinates of a point in three dimensions are a triplet of numbers (x,y,z). The three numbers, or coordinates, specify the signed distance from the origin along the x, y, and z-axes, respectively. They can be visualized by forming the box with edges parallel to the coordinate axis and opposite corners at the origin and the given point.
The points may now be defined in a three dimensional volume of space. This permits to define points in three dimensions from the origin. The Cartesian coordinates (x,y,z) of a point in three-dimensions specify the signed distance from the origin along the x, y, and z-axes, respectively. Z-axis points become the third entry when defining coordinate locations.
Given the above corner-of-room analogy, we could form the Cartesian coordinates of the point at the top of your head, as follows. Imagine that you are five meters tall the z-axis, and that you walk two meters from the origin along the x-axis, then turn left and walk parallel to the y-axis four meters into the room. The Cartesian coordinates of the point at the top of your head would be (2,4,5).
For example, a notation of (2,4,5) corresponds to the value of X2, Y4, and Z5. See Figure 8.
3 Dimensions
Cartesian coordinates can be used for locating points in 3 dimensions as in this example:
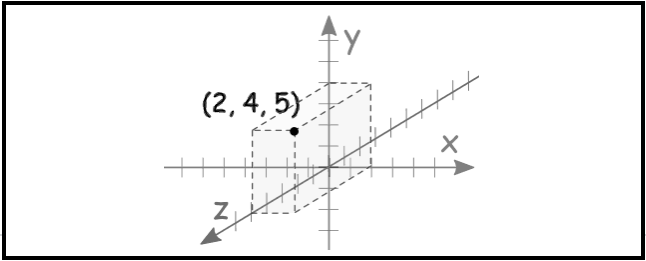
Figure 9. The point (2, 4, 5) is shown in three-dimensional Cartesian coordinates.
Quadrants
The coordinate axes divide the plane into four parts, called quadrants (See Figure 9). The quadrants are number counterclockwise, starting from the upper right, labeled I, II, III and IV with axes designations as shown in the illustration below.
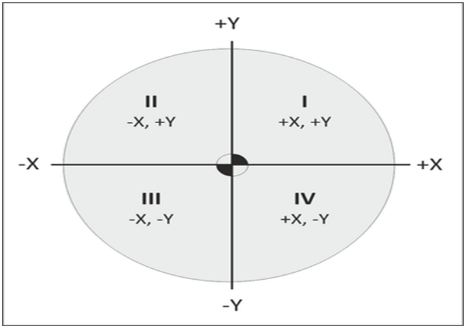
Figure 10
Four Quadrants:
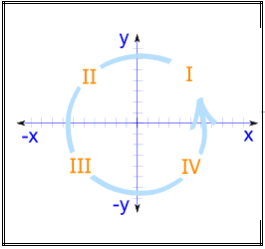
When we include negative values, the x and y axes divide the space up into 4 pieces:
Quadrants I, II, III and IV
(They are numbered in a counterclockwise direction)
In Quadrant I : both x and y are positive
In Quadrant II : x is negative (y is still positive)
In Quadrant III : both x and y are negative
In Quadrant IV : x is positive again, while y is negative
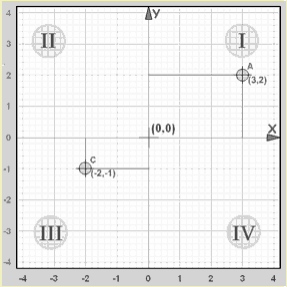
| Quadrant | X (Horizontal) | Y (Vertical) | Example |
| I | Positive | Positive | (3,2) |
| II | Negative | Positive | (-5, 2) |
| III | Negative | Negative | (-2, -1) |
| IV | Positive | Negative | (2, -5) |
Example: The point “A” (3,2) is 3 units along the x-axis, and 2 units up the y-axis.
Both x and y are positive, so that point is in “Quadrant I”
Example: The point “C” (-2,-1) is 2 units along the x-axis in the negative direction, and 1 unit down the y-axis in the negative direction.
Both x and y are negative, so that point is in “Quadrant III”
Dimensions: 1, 2, 3 and more …
1. The Real Number Line can only go:
- left-right
- so any position needs just one number
2. Cartesian coordinates can go:
- left-right, and
- up-down
- so any position needs two numbers
3. 3 dimensions
- left-right,
- up-down, and
- forward-backward
UNIT TEST
1. What is CNC?
2. Describe the cartesian coordinate system.
3. What is The Origin?
4. The Horizontal line is called what?
5. The Vertical line is called what?
6. Describe the real number line.
7. Explain Abscissa and Ordinate.
8. What are the representation of the three axes of the three dimensional cartesian coordinate system.
9. The coordinate axes divide the plane into four parts, is called what?
10. In Quadrant IV, the X axes and the Y axes is what?

