Inverse Square Law
Learning Objective:
- Understand the application of the Inverse Square Law as it pertains to Radiation Safety
- Apply the Inverse Square law to create safe distances, times, or radiation amounts.
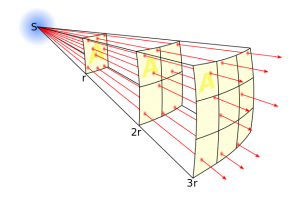
Inverse Square law: The radiation Intensity is inversely proportional to the square of the distance. Notice in the diagram that as the distance doubles, the area quadruples and thus, the initial radiation amount is spread over that entire area and is therefore reduced, proportionately.
Imagine we are trying to expose a piece of x-ray film (radiograph) and we move the x-ray source twice as far away on each shot, will the film be more or less exposed ? Therefore, while the inverse square law pertains to radiation safety, it also helps us to determine source to film distances (SFD), time of x-ray exposure, and the intensity (KV) of our x-ray tube.
[latex]\frac { I _ { 1 } } { I _ { 2 } } = \frac { D _ { 2 } ^ { 2 } } { D _ { 1 } ^ { 2 } }[/latex]
I1 = Intensity with a distance measured as (R/hr or mR/hr)
D1 = Distance with an intensity (usually measured in feet)
I2 = Intensity without a Distance
D2 = Distance without Intensity
To solve for Intensity (I2) means that we want to know what the radiation intensity is at a given, second location or known distance (D2). To solve for Intensity use the following formula:
[latex]I _ { 2 } = \frac { I _ { 1 } x D _ { 1 } ^ { 2 } } { D _ { 2 } ^ { 2 } }[/latex]
To solve for a safe distance (D2), we are calculating how far away from the radiation source (gamma or X-ray) we need to be to achieve either 2mR/hr or 5mR/hr. To solve for a safe distance use the following formula:
[latex]D _ { 2 } = \sqrt { \frac { I _ { 1 } x D _ { 1 } ^ { 2 } } { I _ { 2 } } }[/latex]

