6 Early development
- Overview of early development
- Patterning
- First trimester:
- Pre-implantation
- Gastrulation
- Differentiation of the ectoderm
- Neurulation
- Neural crest cells
- Differentiation of the mesoderm
- Somite formation
- Heart formation
- Differentiation of the endoderm
- Primitive foregut
- Clinical applications of early development

"The Sun photographed at 304 angstroms" is in the public domain CC0Overview of early development
Human development is the process where a single cell, a visually unremarkable cell except for perhaps its size, slowly changes into thirty seven trillion different cells. Embryology is the study of the phases of development, especially the early phases where most of the interesting stuff happens. A round cell, just a ball with no sides and no special parts, grows into an organism with different organs in different places. Fig. 6.1 is the Sun. You see it every day. Can you tell whether the photo is right-side up? Is there even a right-side up? We are not astronomers, but the Sun looks a bit like a fertilized egg, and in Fig. 6.1 there are no obvious landmarks to orient our view. An egg has a similar amorphous (without shape) appearance, but it morphs (smoothly changes shape) into the embryo shown in Fig. 6.2, which has a head-end and tail-end, and clear beginnings of arms and legs. The first part of this chapter focuses on concepts common to many developmental events seen in chapters 7 through 11. The second half of the chapter covers the details of early development.
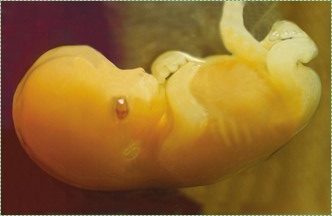
"Human embryo 7 weeks", by GoldenBear is licensed CC BY SA 3.0Pregnancy is divided into three equal time periods named trimesters. During the first two weeks of the first trimester, a single cell multiplies into a multicellular organism with no discernible shape (other than it is a round blob, not an icosohedron). Starting at week 2, the blob of cells develops into an embryo with different shapes. The embryo keeps developing new shapes until it has all of the basic human shapes, such as a head and arms and heart. At this time (week 8) it is a fetus, and the first trimester has ended. The next two trimesters are covered in much less detail.
In this book, we list all times in days, weeks, months or years (e.g. Fig. 6.3). In a developmental biology class, times may be listed in carnegie stages, which are less useful to us (unless you want to discuss crown-rump lengths).


NoBody’s Perfect, a documentary on surviving the teratogenic effects of thalidomide. Image credit: "Filmmaker Niko von Glasow", is licensed CC BY SA 2.0As human cells divide during the first trimester, they make decisions as to their cell fate, which ultimately determines the number and location of arms and legs, head and heart. These decisions involve signals being sent between cells. Errors in these signals lead to congenital disorders (or congenital malformation, or birth defects (but see below)). These can happen without known cause. Or, chemicals may interfere with developmental signals, and we call these chemicals teratogens. Probably the most famous teratogen in the U. S. is the medication thalidomide. If taken by pregnant women at the wrong time, thalidomide interferes with the decision-making processes embryos use to decide where to grow limbs. This causes phocomelia, or malformation of the limbs. For many other countries, the teratogenic effects of agent orange (dioxin, which is also found in cigarette smoke) and atomic radiation (pdf download) are well known, but this information is notably absent in most American school classes (agent orange and atomic radiation also have adverse effects on adults, and the rate this information reaches the American public is subject to similar biases). We will cover a small number of signals involved in important decisions that are made during face and tooth development. 37 trillion decisions are made between the single-cell stage and birth, and errors are inevitable. Some errors are minor, changing the appearance but not the function of an organ; we might refer to this as a birth mark or human variation. Other mistakes are more severe, interfering with a person’s health, and we refer to those as congenital disorders (or perhaps inborn errors of development, but preferably not birth defects, because our choice of words influences the amount of health care people seek, it depends on the patient).
Much of what we cover in this chapter comes from studying the development of animals, some of which don’t even have teeth, like sea urchins, tunicate worms and flies. These model organisms are useful to us for two major reasons. One, they develop quickly, in large numbers, externally (no uterus), and may even be see-though. Two, early developmental processes are highly conserved across metazoans (there have been few mutations to DNA instructions over millions of years). If you don’t think you share much in common with a fly, take a look at your larval stage in Fig 7.1← in the next chapter. We do have significant differences. As a result, sea urchins are much less useful when we discuss traits like a head. Worms and flies are less useful when discussing traits unique to vertebrates, such as teeth and our “new head” (covered in chapter 7).
But for early development (this chapter), experiments on what those of us with new heads often call simpler organisms yields a wealth of useful information. Experimenting on other organisms allows researches to do fate-mapping. In essence, if you inject a stem cell← with a dye, you can follow it as it goes through mitosis← to produce a large number of terminally differentiated adult cells. Any adult cell that contains the dye must have come from that stem cell. This allows us to map the lineage of adult cells. Instead of using dyes, some developmental biologists use chimeras, a technique invented by Nicole Marthe Le Douarin, to identify the diverse roles of neural crest cells. Others transplanted cells from one location to another to see if that altered the fate of those cells, or if those cells altered the fate of their new neighbors.
If you at any time feel like you need more information on embryology, these links are helpful:
- The
Embryology Educationpage- by Dr. Mark Hill at the University of New South Wales, Sydney, Australia
Embryo Images Normal and Abnormal Mammalian Development- by Dr. Kathleen K. Sulik and Dr. Peter R. Bream Jr. at the University of North Carolina School of Medicine.
- The
3D Atlas of Human Embryology- an open-source collection of 3D pdf files (readable using Adobe Acrobat reader) by over 70 different students at the Academic Medical Center, Netherlands.
Patterns
In arts and crafts, a pattern is a repeated form or design. The same is true in developmental biology. This section covers the basic patterns that occur during development (patterning, or pattern formation). These patterns are repeated, often with slight changes (the way theme music is repeated with changes in different scenes of a film). Multiple patterns can overlap. However, it is useful to think about developmental patterns individually, the way you might focus on just the vocals– or cello, or accordion– in a song.

Cloning
Mitosis← produces clones, or identical cells with identical DNA. However, cells differentiate and express different genes to become different tissues and organs. In the first 2 weeks of development, cells divide and produce identical (but smaller) cells. Very soon, cells make decisions as to what they are going to become, and these decisions are coordinated with other cells. Without coordination, an embryo could wind up with two tails and no head.

Differentiation
Differentiation is the process where stem cells← begin to express different genes, causing them to appear and function differently from other cells. All cells in the human body have the same DNA, because all cells copied their DNA from the zygote (a few exceptional cells change their DNA a bit). The zygote is a toti-potent stem cell, transcription factors can potentially bind to and activate any gene. As cells differentiate, they limit their cell fate by putting some genes into deep storage (not actually changing the genetic code, but changing what may or may not be accessible to RNA polymerase).
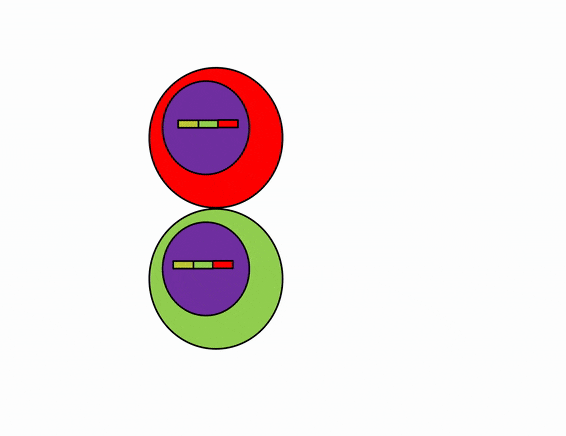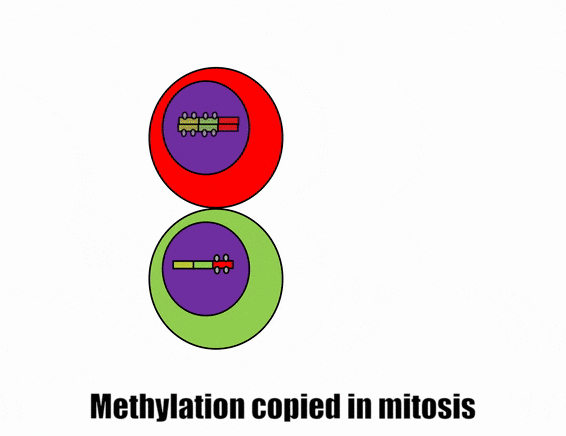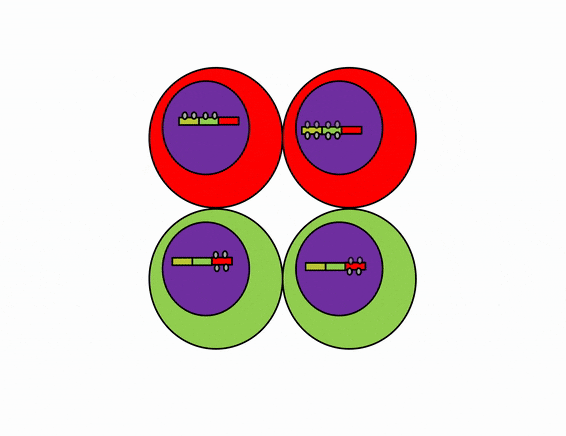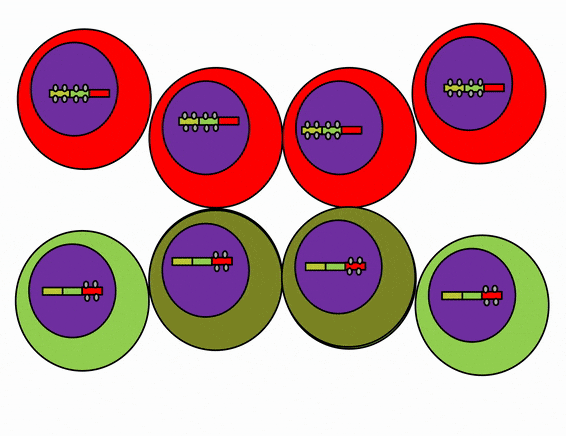
Differentiation is triggered upon receiving chemical signals. These signals activate signal transduction cascades←, which cause target cells to methylate the DNA of un-necessary genes, pack those DNA regions around histones, and permanently shut those genes off. For instance, cells fated to become ovaries never synthesize insulin, the gene for insulin is packaged away long before ovaries secrete estrogen or ovulate. DNA methylation and histone packaging limits the fate of these cells. The methylation pattern is copied during mitosis← and passed to both daughter cells (and to their daughter cells). The significance of this is that causing just one cell to differentiate can affect the fate of millions of cells in the future.
Stem cells in the skin repair skin damage easily. Why can’t we use those stem cells to repair damage from a heart attack or Alzheimer’s Disease? That is the basic question we are addressing. In Fig. 6.7, imagine a signal instructs one cell to methylate green genes, leaving red genes available for transcription. Imagine a different signal does the opposite to the other cell, causing mehtylation of the red gene but leaving green genes open. As the red cell duplicates its DNA, it copies the methylation pattern, so that all of its daughter cells cannot express green genes. Conversely, none of the daughter cells of the green cell can express the red gene. We now have 4 red cells, who belong to one lineage, and 4 green cells who belong to a different lineage. All 8 cells have the same DNA (nature), but not the same DNA methylation pattern (nurture). Further patterning arises as cells transcribe un-methylated genes. In the cartoon, as red cells transcribe the red gene, the red protein acts as a short-range signal which induces nearby green cells to express the dark-green gene. And if expression of the dark green gene made those cells look different, we would say those target cells differentiated further. This organism has become more complex, starting as 1 cell type but now having 3 different cell types. This continues until we have 200 or so different cell types. Generally speaking, as a cell becomes more specialized, its fate becomes more limited (more DNA methylation and histone packaging), possibly to the point of being limited to just one cell type.
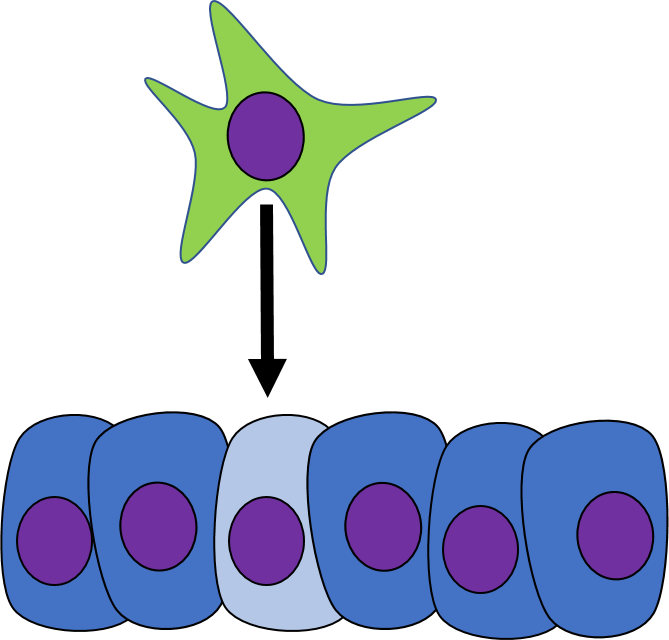
Induction
One cell may signal to another cell and induce (instructs) that cell to differentiate. Chemicals that induce another cell to change its shape (to morph) and change cell fate are called morphogens. Some morphogens are referred to as growth factors, depending on how they were discovered. During early develoment, cells are both growing and differentiating. Morphogens are re-used during regenerating and healing in adulthood, if the chemical signals were discovered in this context, they are more likely referred to as a growth factor. Morphogens are similar to neurotransmitters or hormones, they often bind to cell-surface receptor proteins. Activation of morphogen receptors leads to activation of signal transduction cascades← in the cytoplasm, which in turn can either activate or inhibit specific transcription factors to alter the expression of different genes. Changes in gene expression cause the target cell to look and function differently. Morphogens also change the methylation of genes and their packaging around histones, which is a more permanent change to gene expression. This is passed down to daughter cells, which we learned in Chapter 1 is an example of epigenetic inheritance. By regulating gene expression through both transcription factor activity and methylation, morphogens change not only the morphology the target cell, but their cell fate as well.
There are often several closely-related molecules that belong to a family of morphogens, each chemical having a name like morphogen-1, morphogen-2a, morphogen-2b, and morphogen-3. There are a large number of different morphogens. In this textbook we discuss 4 by name, ones directly related to tooth development, such as the Bone Morphogenetic Protein (BMP) family, the Wingless/Int-1 Wnt family, and the Fibroblast Growth Factor (FGF) family. Morphogens can act over different distances listed in Table 6.1. The names of specific morphogens are very important on embryology exams, much less so on dental hygiene exams.
| Distance | Type | Examples |
|---|---|---|
| Direct | Cell-to-Cell | Epithelial-to-neuro-mesenchymal stem cell (Odontoblast differentiation) |
| Cell-to-ECM | Integrin-to-collagen (Ameloblast differentiation) | |
| Short-range | Diffusion through ground substance | Bone Morphogenetic Protein (BMP), Wnt, Fibroblast Growth Factor (FGF) (tooth bud induction) |
| Body-wide signals | Hormones | PTH, Calcitonin (tooth eruption) |
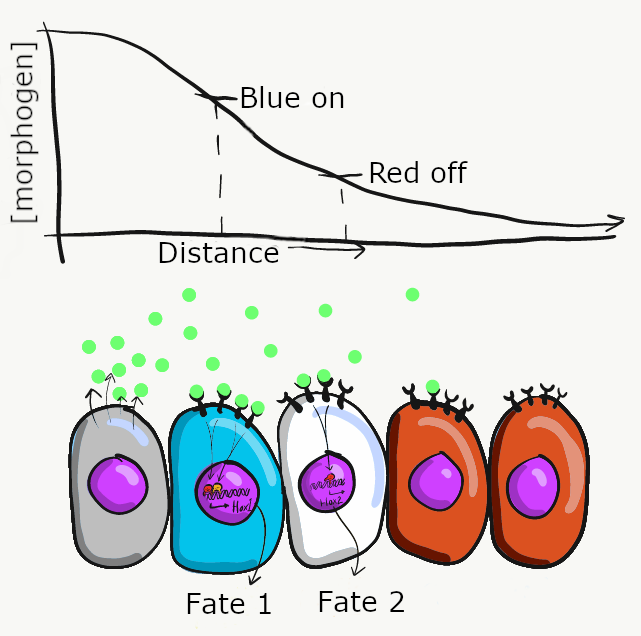
Morphogens are secreted into ground substance←, creating a concentration gradient of morphogen levels as they diffuse slowly away from the source. The amount of morphogen molecules produced, the relative stickiness of the ground substance, the distance away from the source and the number of receptor proteins on the target cell determine level of a signal cells receive. Sometimes, a morphogen produces visible effects that fall along a linear gradient (or spectrum), such as skin color (from lighter to darker) or body size (from shorter to taller). However, sometimes the effects of a morphogen are more discrete (tooth bud or no tooth bud, there are no half tooth buds). To help explain these observations requires a little knowledge of how transcription factors work. For example, in the French flag model (Fig 6.9), imagine receiving high levels of the morphogen signal triggers the transcription of a blue gene and inhibits a red gene, causing those cells to differentiate into blue cells. Moderate amounts of the morphogen signal may not be enough to recruit RNA polymerase to the blue gene, but enough to bring inhibitory transcription factors to the red gene, causing cells in regions of moderate morphogen levels to differentiate into white cells. Lastly, cells that receive little or no morphogen signal do not inhibit the red gene, causing them to differentiate into red cells. There are other models that help explain the link between induction and morphogenesis (such as a morphogenetic field ). These models all share an important concept: chemical signals can communicate positional information in a developing embryo.
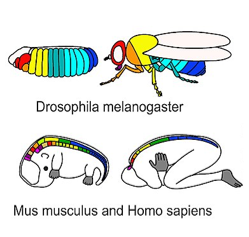
Hox genes in various species" by Stefanie D. Hueber, Georg F. Weiller, Michael A. Djordjevic, Tancred Frickey is licensed under CC BY 4.0 / croppedDuring very early development, regional expression of homeobox genes controls cell fate, not morphology (further reading). Homeobox genes are transcription factors that specify which part of the body a particular cell is now a part of along the anterior-posterior axis, even if that area has no specific shape yet (Fig. 6.10, upper left). They do not encode the proteins which cause cells to become part of a specific organ. Instead, homeobox genes activate or inhibit a collection of other genes (a program), setting the stage for future changes. Such programs include morphogens like FGF and BMP, which activate genes that alter cell and tissues morphology (Fig. 6.10, upper-right).
Homeobox gene expression represents a very specific plan in embryology. It is highly conserved across animal species, and the pattern is very predictable in embryos. The pattern is also relatively simple and linear (Fig. 6.10). Think of homeobox genes like surveyors who determine the locations where houses will be built in a subdivision, while morphogens are the contractors who follow the DNA blueprints for each house, which are built by cells. We can extend this metaphor one step further: in a subdivision, houses are similar, derived from one basic blueprint, but given slight modifications with each re-use.
Lastly, it is important to note that in embryology, the anterior-posterior axis means head-to-tail, the same way it is used in all forms of animal biology except adult humans, where it means front-to-back. You may also hear the term rostral-caudal applied to human embryos, but not human adults (except their brains).

Self-organization
The ability of a tissue to create its own patterns is called self-organization (in contrast, maternal effect genes from mom’s cells guide patterns for the embryo). The French-flag model describes how one morphogen can induce multiple cell fates. But what if you want a flag with repeating stripes? Self-organization involves multiple morphogens, initially expressed randomly. Interactions between these morphogens leads to a stable pattern of expression, and a complex pattern of differentiation.
For instance, some morphogens block cells from producing the same morphogen. In Fig. 6.11, imagine a blue morphogen induces one cell to differentiate into a blue cell, but blocks neighboring cells from becoming blue cells. These neighbors would be free to differentiate into red cells. At the same time, a distant cell produces red morphogen, which induces it to differentiate into a red cell, but blocks its neighbors from doing the same. Its neighbors would be free to produce blue morphogen and differentiate into blue cells. The initial pattern that arises is alternating rings of red and blue cells. However, rings produce regions of red-next-to-red and blue-next-to-blue, which violates our make-believe rules, and this starts a battle. To minimize the number of red-next-to-red and blue-next-to-blue, cells change their cell fate until a stable pattern arises, in this case stripes. It would be hard to predict from the start which cells would be red versus blue, but you could predict the development of red and blue stripes. If these were pigment-producing cells in a zebra, we’d have a zebra with stripes (the best type of zebra). But this pattern could also be alternating regions of oral mucosa that grow a tooth bud or don’t grow a tooth bud, ensuring each tooth bud has enough space to grow (these interactions can be modeled mathematically). When a morphogen blocks another signal, we call that antagonism, and antagonist signals are just as common as induction signals. It is fundamentally just as important to grow one head as it is to not grow two heads.
Proliferation
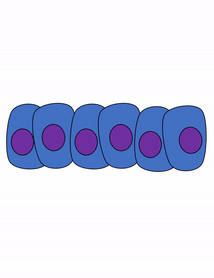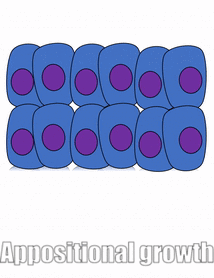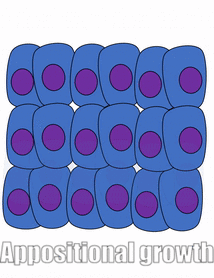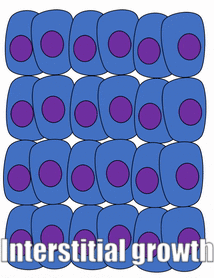
Growth of a tissue is called proliferation. Proliferation occurs either by mitosis← (adding cells) or by adding ECM (synthesizing proteins or other molecules). When new growth happens next to a region of older growth, this is appositional growth, whereas if growth happens from within and pushes older tissue outwards, that is interstitial growth. Dense tissues, such as bone←, enamel and dentin, undergo appositional growth. Softer tissues like mesenchyme← grow interstitially.
The growth of an organ is regulated by hormones, such as Growth Hormone, which coordinates the rate of growth of tissues body-wide. On the other hand, local-acting morphogens cause small regions to grow faster than neighboring regions. To make room for new cells while still maintaining a single-layer of cells connected to neighbors by desmosomes←, CAMs← and tight junctions←, an epithelium bulges inwards or outwards if it can’t grow wider. An outward growth is known as a bud, and an inwards growth is an invagination. Arms and legs grow from buds, while teeth, hairs and the brain grow from invaginations. These are both forms of interstitial growth.
When we learned about the histology of epithelia, we said epithelia are located on the outer or inner surface of the body, with the apical side facing a space and the basolateral side next to connective tissue (junctional epithelium being an exception). It is simpler to form a new epithelium by folding an old one, as the process of folding creates a new space. Otherwise, if you tried to form a new epithelium in the middle of other stuff, that would either require re-programming the cells’ apical-to-basolateral polarity, or first digesting a new space and then guiding epithelial cells to its location. Folding is simpler, it creates a space right where you need it (apical), and as a result you will see a lot of invaginations in the next three chapters.
Kunstformen der Natur (1904), plate 1: Phaeodaria“, by Ernst Haeckel is in the Public Domain CC0Morphogenesis
Morphogenesis is the appearance of new shapes in an organism. It means to go from no shape to some shape. The word morphology can mean the study of these shapes, or be used as an adjective to mean the shape of something (For example, a cleft palate← is a change to the healthy morphology of the palate). From the zygote to the blastula stage (sometimes referred to as the germinal stages) the ball of cells is amorphous. At the start of gastrulation, however, the embryo undergoes numerous morphological changes. New shapes arise in the developing embryo. It develops an inside and an outside, a tail end and a head end, a left and right, and a front and back. After that, a nervous system and a circulatory system become visible. How long do you think it takes before teeth develop? The answer may surprise you.
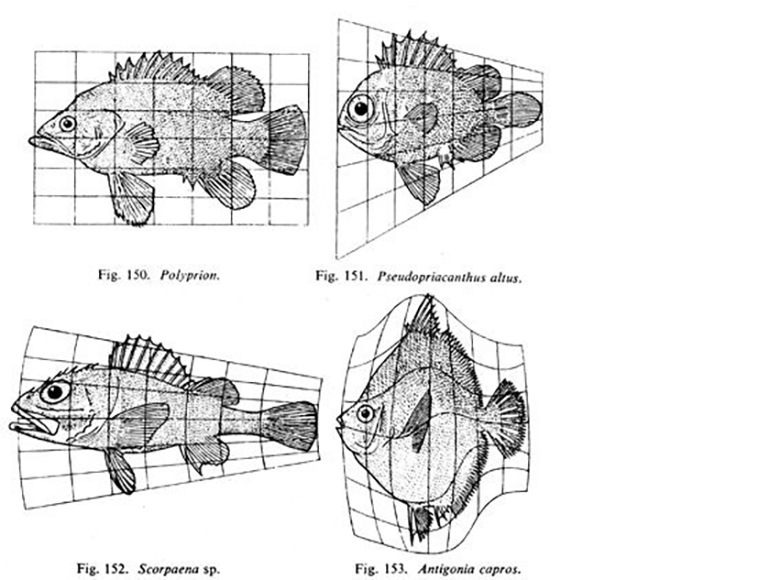
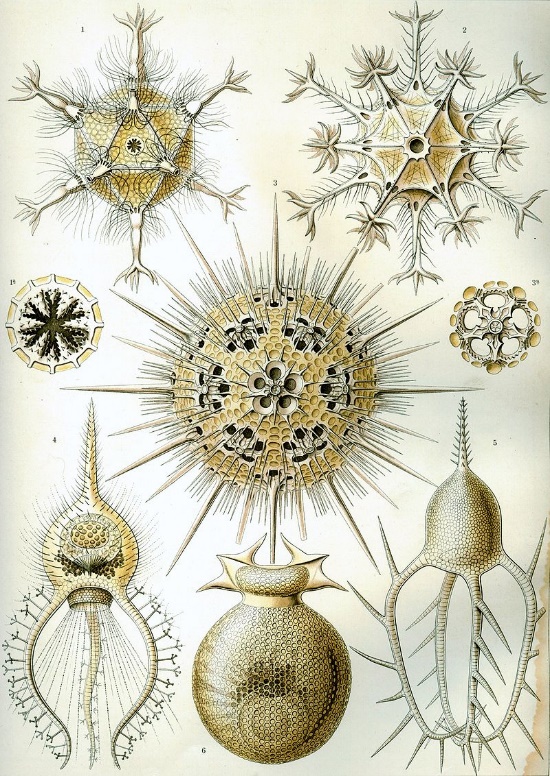
"Fig 150-153" by D’Arcy Wentworth Thompson, On Growth and Form is in the Public Domain, CC0Fig. 6.14 is a famous drawing of tiny sea creatures with mineralized exo-skeletons. This image was later analyzed by a mathematical biologist named D'Arcy Wentworth Thompson, who noticed different biological shapes can be different transformations of the same shape. Transformations, he proposed, occurred by different localized rates of growth– something our current knowledge of morphogen signaling supports. This is what he illustrated in Fig. 6.15. He is regarded as the first person to describe morphogenesis. When Thompson looked at the tiny sea creatures, he didn’t see different shapes, he saw variations on one shape. These variations arose over evolutionary time, and led to different-looking sea creatures (who share lineage). In this book, we look at different body parts that share the same lineage but change over developmental time, such as hair follicles and tooth buds. Thompson’s ideas were expanded upon by the mathematician Alan Turing, who coined the term morphogenesis. His other achievements include inventing computer science and breaking the Nazi code during WWII (with the help of many female mathematicians at Bletchley park).
Morphogenesis and genetics
To have a well-rounded understanding of how morphogen signaling works, it helps to understand some concepts of genetics. When we say understand, we don’t mean memorize the specific details, instead focus on the concepts. First, pay attention to when we use the word morphogen, because we likely mean the signaling molecule itself. We at times discuss the morphogen signal, and that extra word signal makes a big difference. Mutations that alter morphogen signals include mutations to the gene for the extra-cellular morphogen molecule itself (if it is a protein such as FGF or BMP) or enzymes that synthesize the morphogen (such as the conversion of carotene into Retinoic Acid), cell-surface receptors for the morphogens, cytoplasmic second messengers and nuclear transcription factors. Discussing morphogen signaling levels saves us from the complexity of having to mention the entire signal transduction cascade←. Next, some mutations might be gain-of-function, such as a mutation to a receptor that prevents it from shutting off, and these are often inherited in an autosomal dominant fashion (it only takes 1 faulty allele to create a signal where it shouldn’t be). Alternatively, loss-of-function mutations prevent proteins from functioning properly, and are often inherited in an autosomal recessive pattern (it takes both copies to be faulty to lead to a loss of a signal where it should be, one good allele would be enough). Some mutations fully stop, or fully start, morphogen signals. In such cases we say theses mutation have complete penetrance. Other mutations might partially block or partially start morphogen signals, and have partial or incomplete penetrance. The severity of the symptoms fall on a spectrum.
"Generalized scheme of embryonic development" by JMW Slack is licensed CC BY SA 4.0Maturation
Maturation is the process by which new shapes created by morphogenesis continue to develop and take on a more mature (adult-looking) form. By the end of week 9, all of the basic organ shapes have formed, and we say the embryonic period is over and the fetal stages begin. The fetus undergoes maturation, and maturation involves bits of the previous processes (another way of saying that is maturation recapitulates other developmental processes).
Fusion
Sometimes, two separate bits of the same type of tissue come into contact with one another and fuse into a single tissue. For an epithelium, this requires the cells share the same type of CAM←. For a connective tissue, this requires the correct integrin← binding to the correct fibronectin←. In Fig 6.17, the basic pattern of green being on the outside and red in the middle is initially disrupted by the fusion of two structures. There are three ways to remove green cells from the middle area. The first way is for cells to receive guidance cues and cause cells to migrate. Some guidance cues are repulsive, such as the lack of correct cell-to-cell contacts←, or high concentrations of a repulsive morphogen (if you are at a party and leave the living room because someone there smells bad, you are acting on a repulsive guidance cue). Other guidance cues are attractive, such as the correct cell-to-cell contact or a positive guidance morphogen (at the same time, you smell delicious hors d’oeuvres in the kitchen and head there, you are acting on an attractive guidance cue). Whether a cell-to-cell connection or morphogen is attractive or repulsive depends on how the target cell has been programmed (what receptor genes it is expressing). The second way to remove cells from the wrong location is to induce them to undergo apoptosis← (see below). Lastly, another way to re-organize cells is to induce them to de-differentiate (revert to a stem cell←) and then differentiate into the correct cell type. This is called a transition; both early development and tooth development involve examples of epithelial-to-mesenchymal transitions and mesenchymal-to-epithelial transitions (discussed later in this chapter).
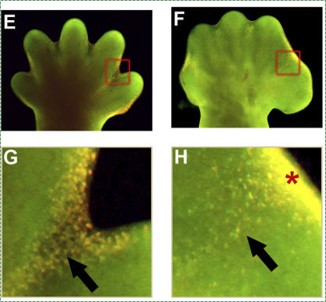
"Depletion of BMP Signaling Causes Interdigital Syndactyly", by Bandyopadhyay A licensed CC BY SA 4.0Apoptosis
Cell death is necessary for multicellular life. In the construction of tall buildings or large ships, scaffolding← is built first to allow construction workers to get where they need easily, and the scaffolding is removed after construction is complete. Similarly, during development, apoptosis← is an integral part of the construction of body parts. Many tissues grow more cells than are needed in the mature form. To undergo maturation, un-needed cells undergo apoptosis←. For instance, during the growth of bone tissue, cartilage tissue is made to act as a scaffold for osteoblasts. Shown in Fig. 6.18, the hands and feet start off as limb paddles, and only with apoptosis in alternating regions does the morphogenesis of fingers and toes occur. Without enough apoptosis, people are born with webbed fingers or toes, or suffer ankyloglossia (their tongue is tightly anchored to the floor of the mouth by a pronounced lingual frenulum).
The first trimester

"Fertilization in humans", by Ttrue12 is licensed CC BY SA 3.0Pre-implantation period
The pre-implantation period begins with fertilization, spans a week or so of development, and ends with an embryo implanting into the uterus. Fertilization is the union of one sperm cell and one egg– thousands of sperm are needed, but only one is allowed into the egg. This union joins 23 maternal chromosomes with 23 matching paternal chromosomes, forming a zygote. Fertilization most often occurs towards the distal end of a fallopian tube. Over the next week the zygote undergoes mitosis← and increases in cell number, but does not grow in size. All of the amino acids and nucleotides for making new cells during this first week come from the cytoplasm of the zygote, which is why the egg is a very large cell. After implantation, the uterus provides the raw materials for an embryo to grow larger.
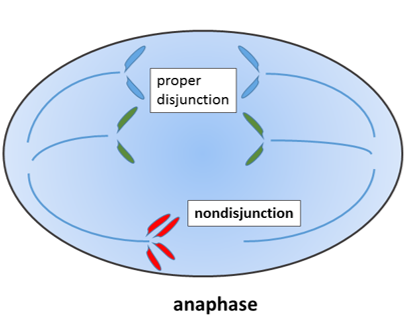
"Non-disjunction of sister chromatids", by Wpeissner is licensed CC BY 3.0During mitosis←, the 23 pairs of chromosomes are duplicated and divided between 2 daughter cells evenly. If mistakes are made and an odd number of chromosomes wind up in a daughter cell, this fails a cell cycle checkpoint and triggers apoptosis←. If a chromosome breaks, it can lead to the same result.

"Boy with Down Syndrome using cordless drill to assemble a book case" by Rob Kay is licensed CC BY SA 3.0There are exceptions, however. A cell with an odd number of chromosome 21 or 23 can survive. If that cell is the egg, then the zygote and all subsequent cells will have an odd number of chromosomes. This leads to congenital disorders such as Trisomy 21. If the chromosomal segregation error happens at the 2-cell stage of development, then only half of the cells in the adult would have an extra chromosome, and the condition would be less severe. Extra chromosomes interfere with decision-making processes in development. People with Trisomy 21 frequently develop microdontia, and may suffer from hypo-salivation and bruxism. They therefore need to engage in extra care to maintain healthy oral hygiene.

Early divisions
During the first week of development, the zygote undergoes 3 cleavage divisions, where mitosis← occurs in a synchronized fashion. You can watch a cool video here, as you do see how the embryos are oriented in the same direction. Is the lower half of zygotes heavier? To answer that, frog astronauts helped NASA scientists study early development on the space shuttle. Both on earth and in space, cells duplicate along single planes, 3 times, producing an 8-cell embryo (suggesting density and gravity are correlated with early cell polarity but do not cause polarity). Synchronizing mitosis requires cell-to-cell communication between gap junctions to coordinate cell cycle checkpoints. Synchronized mitosis leads to the embryo developing symmetrically. As mitosis continues, the number of cells continues to double, but the cells do not divide along the same plane. This forms a solid ball of cells called a morula. As mitosis continues, cells continue to get smaller, until the solid ball of cells becomes a hollow ball of cells named a blastula (or blastocyst). From the zygote to the blastula stage, cells appear no different except in size. A fancier way to say this is that there are no changes to morphology. During the blastula stage, a group of cells named the inner cell mass move away from the others. The fate of the inner cell mass is to become the embryo, while the outer cells, known as the trophoblast, are fated to become extra-embryonic structures such as the amnion and part of the placenta. Therefore, taking a DNA sample by amniocentisis allows for the analysis of fetal DNA without affecting the fetus itself. The blastula implants in the endometrium about a week after fertilization and continues developing.
Gastrulation
It is not birth, marriage, or death, but gastrulation, which is truly the most important time in your life.—Lewis Wolpert.

Gastrulation overview
During gastrulation, the embryo is reorganized from a single layer of undifferentiated cells into three layers of differentiated cells. Some of the cells from the single-layered blastula invaginate, forming a layer of cells on the inside and a layer of cells on the outside of the embryo. The significance of this is that this is the first instance where embryonic cells look different from one another. It is also the first instance where cells limit their cell fate. But, wait, if all the blastula cells are identical, why did only some of them migrate? Mitosis← generates two cells with identical DNA, but not necessarily identical cytoplasm. If an egg has mRNA for a transcription factor clustered into one spot in the cytoplasm, the first cleavage division produces two non-identical cells, one with the transcription factor mRNA and one without. Later, when the mRNA is translated, it could induce that cell to migrate inwards, while other cells stay on the outside. NASA’s frog astronauts taught us that transcription factors don’t sink in response to gravity to induce gastrulation. Instead the difference is a maternal effect. An mRNA for a transcription factor, not transcribed from the zygotes’ DNA but made by mom’s ovary cells, is deposited into a specific part of the egg’s cytoplasm, and it induces some cells to invaginate during gastrulation. In fact, up through the blastula stage, the embryo hasn’t used any of its own DNA. Because the embryo’s DNA is not guiding gastrulation, this is yet another example of an epigenetic trait.
Let us return to gastrulation: it first generates two layers of cells (outside and inside). Imagine holding a tennis ball and pushing your thumbs inwards, forcing some of the outer rubber to fold inwards. The tube that forms becomes the gastrointestinal tract, and the opening (can you guess?) becomes the anus. The embryo therefore now has a distinct tail direction and head direction. Fig. 6.23 looks more like the way a sea urchin undergoes gastrulation. Human embryos look different because it is only the inner cell mass that undergoes gastrulation, not the entire blastula. But the 2 layers are the same, human gastrulas simply look more squashed. Oh, and sea urchins don’t form anus-first. We are sacrificing accuracy here to focus on important concepts shared across our species. If you are curious, watching movies of these processes in humans is not possible, but it is for organisms like xenpous laevis (frogs).

During gastrulation, another important event occurs, cells from the outer layer migrate between the two layers that formed by invagination. This now gives the embryo 3 layers, which are the three embryonic germ layers (Fig. 6.23). The outer layer of ectoderm and the inner layer of endoderm remain epithelial in appearance, while the middle layer of cells (mesoderm) undergoes a morphological change, and becomes mesenchyme←. This migration begins at a single location called Hensen's node (or the Spemann organizer). which moves down the embryo forming the primitive streak behind it (Fig. 6.24). The side of the embryo with the node is fated to become the dorsal side, and the streak divides the embryo into a left-half and a right-half. You have now witnessed, in cartoon form, how something (all the basic body directions) arose from nothing. Don’t let the significance of this sneak past you. Scientists have a hard time explaining what there was before the universe formed, or how the Earth went from having no life to having life. Embryologists, by contrast, explain how embryos change from having no shape to having shape in great detail (we have the benefit of watching and manipulating this process).
| 3 embryonic layers | Cell fate |
|---|---|
| Ectoderm | Epithelium of skin and oral mucosa, neural tissue |
| Mesoderm | Connective & muscle tissue |
| Endoderm | Epithelial lining of hollow organs |
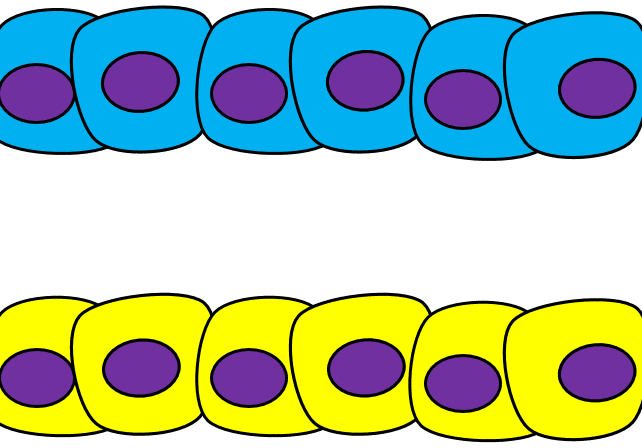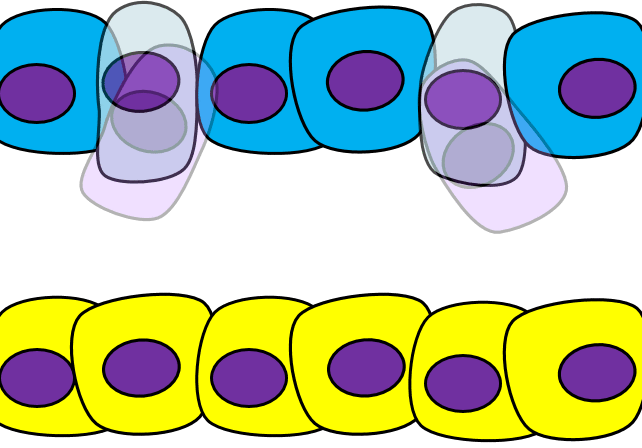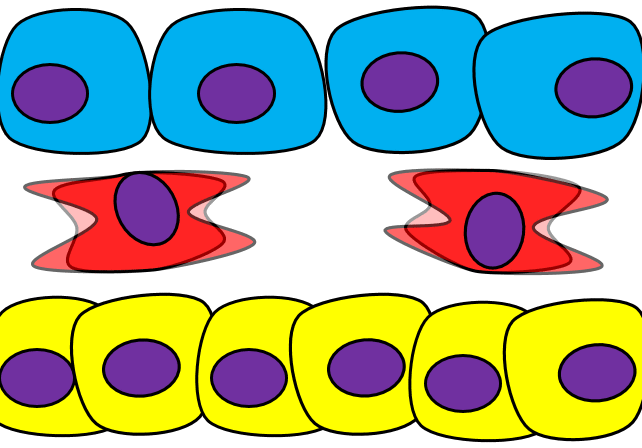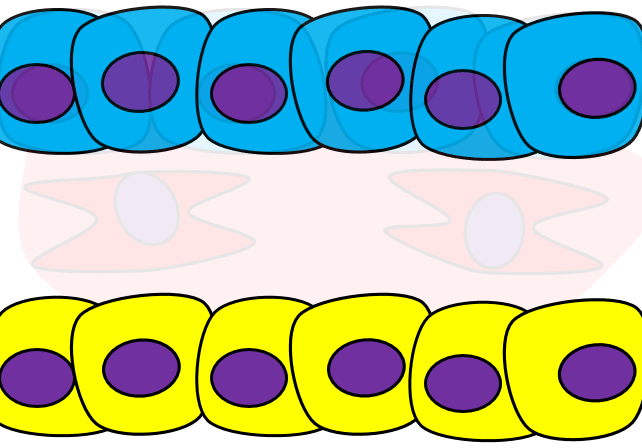
Epithelial-to-mesenchymal transition
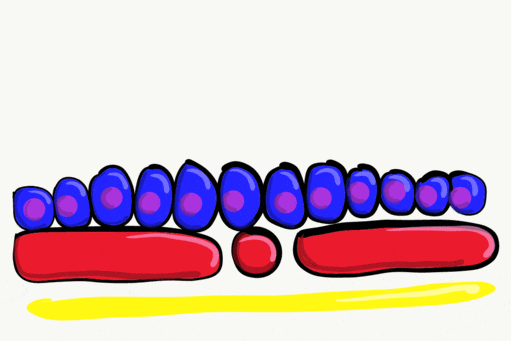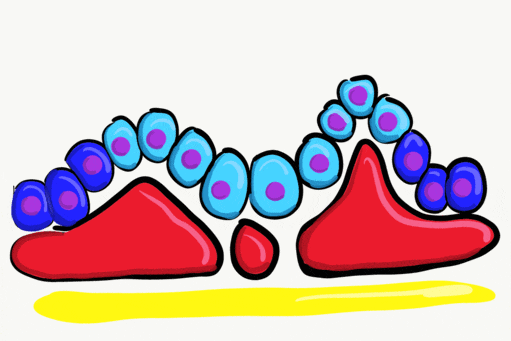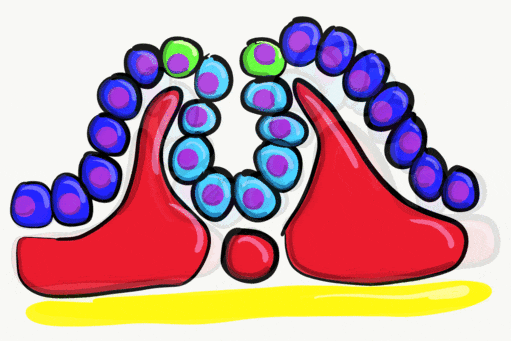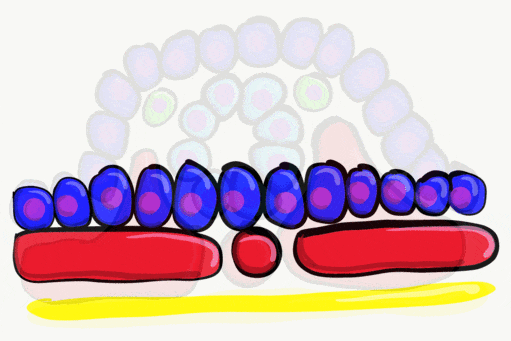
The formation of endoderm from ectoderm was a simple matter of invagination. The process by which ectodermal cells quit being ectoderm and migrate to the middle to form mesoderm is called an epithelial-to-mesenchymal transition (EMT). The epithelial cells of the ectoderm first lose cell-to-cell contacts← with neighboring cells, which makes them less epithelial. They lose their polarity, de-differentiate into stem cells←, then differentiate into mesenchymal stem cells. This process is not only required to form mesoderm during gastrulation, it occurs during neural crest cell← migration, wound healing, and cancer metastasis. There is a reverse process, called a mesenchymal-to-epithelial transition (MET), which also occurs during wound healing. EMT allows epithelial stem cells from a healthy region of oral mucosa to turn into mesenchymal stem cells, migrate away from the healthy region into the damaged region. MET then allows the mesenchymal stem cells to turn back into epithelial stem cells, which divide and differentiate into new keratinocytes. Because this mimics what happens during gastrulation, we say “wound healing recapitulates development”.
Differentiation of ectoderm
Neurulation
Gastrulation gave the embryo its first polarity, as well as the beginning of the GI tract. One of the next organ systems to develop is the central nervous system. The basic process used in neurulation is recapitulated when other hollow organs form (watch another cool video here). During the 4th week of development, underlying mesoderm known as the notochord releases morphogens which signal to nearby ectodermal cells. This induces the nearby region of ectoderm to differentiate into neuro-ectoderm, followed by local proliferation. Because these epithelial cells cannot easily spread side-to-side, they invaginate. Ultimately, invaginating neuro-ectodermal cells lose their contacts with the ectoderm and fuse to other neuro-ectodermal cells, creating a new structure called the neural tube. This tube develops into the brain and spine. If you are wondering about the notochord, its cell fate is to mostly undergo apoptosis←, although some remains as the nucleus pulposis of the vertebral discs. In headless fish-like chordates with no backbone called amphioxis, the notochord remains. This wont be the last time you see a human embryo make a structure only to remove it.
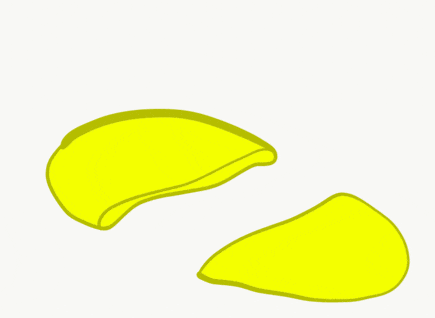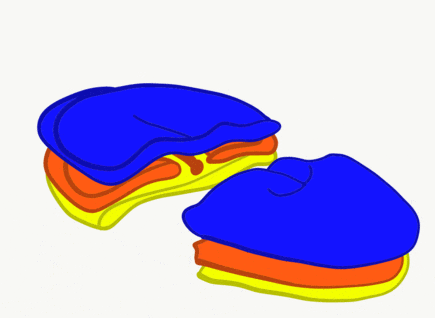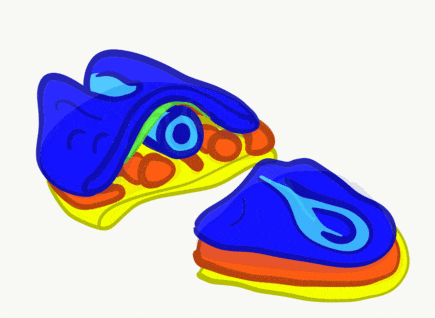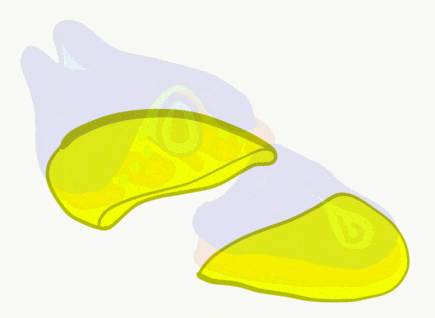
The neural tube begins folding from the anterior portion of the embryo, and zips up in an anterior-to-posterior direction. The zippering is not perfect because the anterior end is growing wider as it is folding to form the primitive brain. For almost all developmental processes, the anterior end is the region that develops first, followed by more posterior regions. Zipping the neural tube requires adequate levels of folic acid (which is needed for the DNA methylation and differentiation), so hopefully mom’s melanin did an adequate job protecting it.
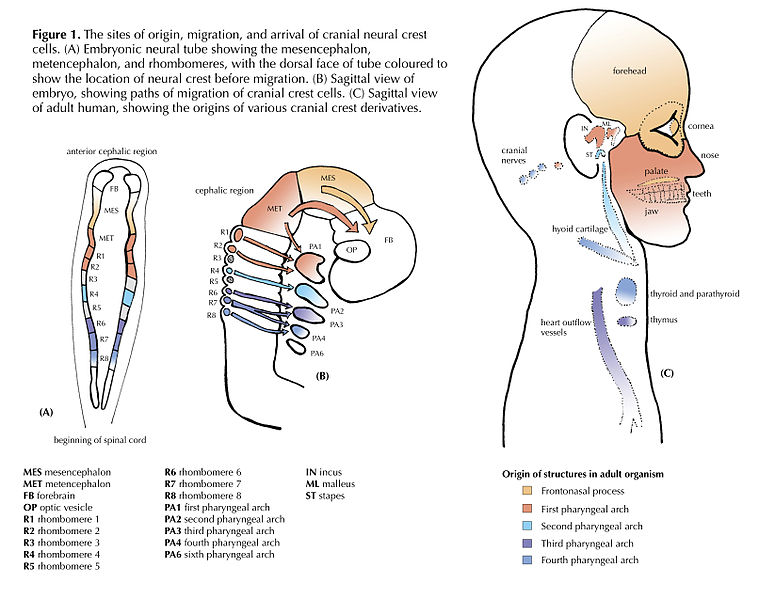
"Cranial Neural Crest Cells - migration" by BiolCNC is licensed under CC BY-SA 3.0Some neuro-ectoderm cells do not fuse. Instead, these cells undergo an epithelial-to-mesenchymal transition and migrate away from the neural tube. These cells are neural crest cells, they are fated to become a number of important cells and tissues throughout the body including melanocytes, odontoblasts, dental pulp, cementoblasts, and the neuro-mesenchyme of the pharyngeal arches←. These cells are sometimes referred to as the fourth embryonic tissue (in addition to the three embryonic germ layers that arise during gastrulation), which suggests some people think neural crest cells are important. Even after neural crest cells migrate to new and distant tissues, they often retain visible signs of their neural lineage, such as the dendrites on melanocytes or the odontoblastic process of odontoblasts. To make migration easier, neural crest cells express a matrix metalloproteinase enzyme. This enzyme digests proteins found in the ECM. By now we hope remember the phrase wound healing recapitulates development. Matrix metalloproteinase enzymes are re-used to heal certain types of tooth wounds, but can also be involved with the breakdown of the PDL and loss of alveolar bone tissue.
When neural crest cells reach the pharyngeal arches, they secrete FGF and BMP morphogens, which antagonize each other, producing a striped pattern along the ectoderm. Some regions are induced to form tooth buds←, the in-between regions form oral mucosa.
Differentiation of mesoderm
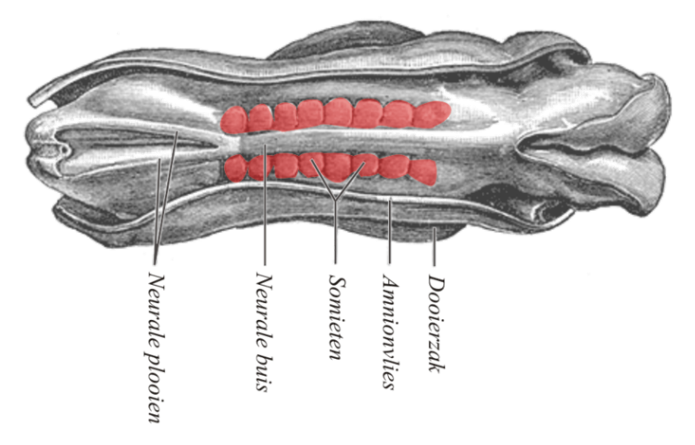
Somite formation
During the same time as neurulation, mesoderm undergoes differentiation. Mesoderm starts off as an amorphous layer of mesenchyme←. Then, regions of mesenchyme pinch off in repeating spherical structures called somites, forming segments along the anterior-to-posterior axis of the embryo. The fate of the somites is to become solid organs, either repeating units of connective tissue such as the ribs and vertebrae, or repeating units of muscle tissue such as the rectus abdominus and intercostal muscles. The formation of each somite involves a mesenchymal-to-epithelial transition, some mesenchymal stem cells differentiate into an epithelium that separates one somite from the next. Because they form in left/right pairs, the production of matching lateral structures is relatively simple (such as left and right biceps brachii muscles). On the other hand, formation of a single structure from somitic mesodem (such as one sternum) requires fusion of two bilateral structures.
There are other regions of mesoderm besides somites and notochord, such as splanchnic, lateral plate and paraxial mesoderm. Differentiating between all types of mesoderm is not essential for understanding clinical concepts in dental hygiene.
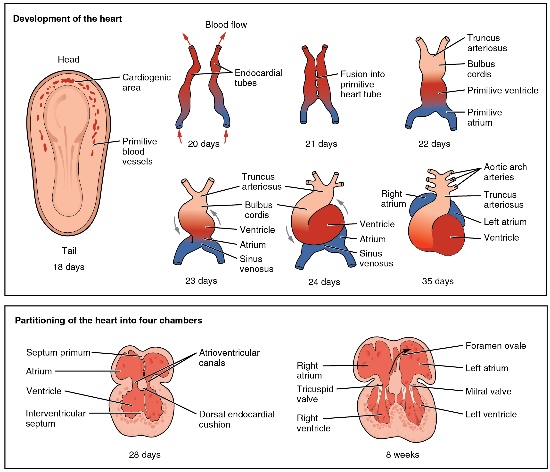
illustration” by OpenStax, is licensed CC BY 3.0Formation of the heart
In the 3rd week of development, mesoderm begins to develop into blood, the heart and the circulatory system. Mesenchymal stem cells first differentiate into blood islands. Next, angiogenesis begins. Two large blood vessels fuse– with some help from neural crest cells— to form the primitive heart, which begins beating.
Differentiation of endoderm

"Time line of mouse liver development emphazing it" by Zorn, A.M., Liver development, StemBook is licensed under CC BY 3.0Formation of the pharynx
The endoderm that migrates interiorly during gastrulation extends its way towards the anterior end of the embryo. This forms the primitive foregut, which later becomes the pharynx. The term “primitive” is used because it has only one opening, there are no oral or nasal cavities. Those develop later from ectoderm. Formation of the face and pharynx are covered in detail in Chapter 7.

4th week
We are now only up to the 4th week of development. A lot has happened! At this time, the embryo continues to undergo local regions of proliferation, patterning, fusion and the other processes covered at the beginning of the chapter. This leads to the formation of rudimentary (basic) structures. When a structure first becomes visible from the surface of an embryo, it is often called a placode (an ectodermal thickening). The cells in a placode are fated to become an organ, but their overall shape is no more than a raised bump or shallow pit. By the 4th week, head-related organs listed in Table 6.3 begin to develop.
| Structure | Fate |
|---|---|
| Optic placodes | primitive eyes |
| Otic placodes | primitive ears |
| Nasal placodes | primitive nose |
| Pharyngeal arches | so many things they get their own chapter |
| Oro-pharyngeal membrane | primitive mouth (not open yet) |
Clinical applications of early development
Disturbances in these early stages of development are usually so severe the embryo does not survive to become a fetus, let alone be born. However, clinical conditions exist related to these early stages and to oral health.
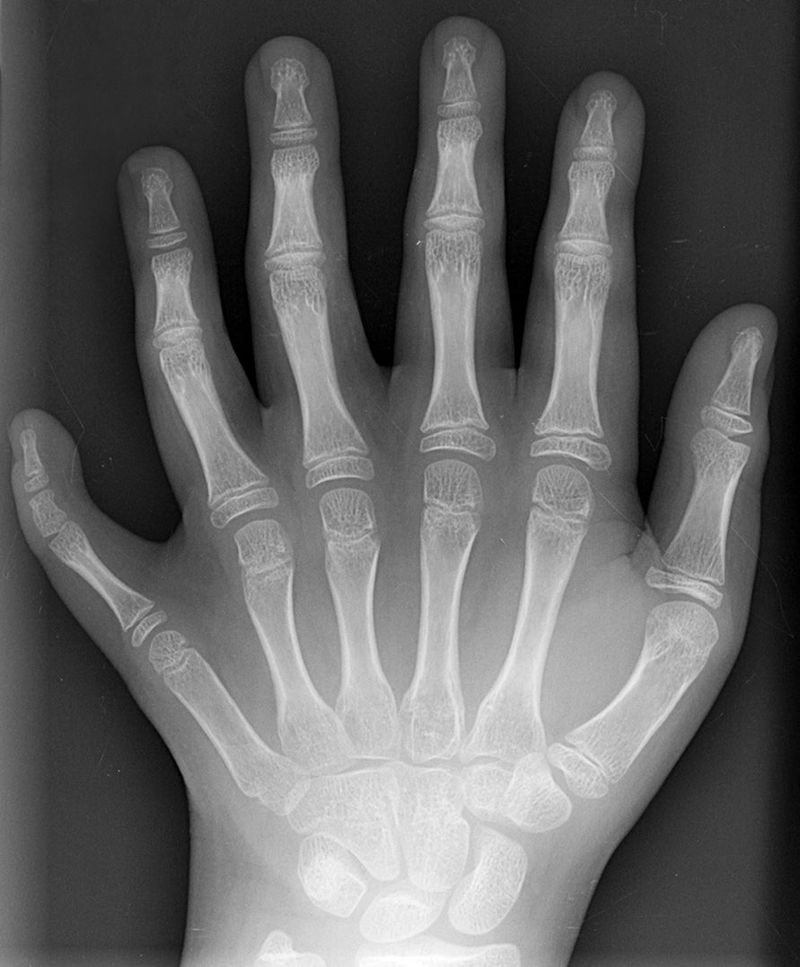
Polydactyly 01 Lhand AP" by Drgnu23 is licensed under CC BY-SA 3.0Homeobox gene mutations
Mutations to homeobox gene can cause entire structures to be missing, or to develop in the wrong location. Early experiments on flies led to observations of legs where antennae should be located, or antennae where wings should be located. There are a few homeobox-related genetic disorders in humans. Homeobox-related disorders are rare because the mutations are usually lethal, but when they aren’t the conditions are often severe. A small list is found in Table 6.4
| Syndrome | Homeobox gene involved | Symptoms include |
|---|---|---|
Axenfeld-Rieger Syndome |
FOXC1, PITX2 | Mostly eye-related, sometimes hypodontia and microdontia |
Autosomal dominant syndactyly |
HOXD13 | Syndactyly (fused fingers or toes) |
Guttmacher syndrome |
HOXA13 | Polydactyly (extra fingers or toes) |
Ectodermal dysplasia |
HOXC13 |
Absent or under-developed hair follicles, teeth, nails and/or sweat glands
|

"Hand of a child with Apert syndrome" by Gzzz is licensed under CC BY-SA 4.0Apert syndrome
Apert syndrome is caused by a mutation in the receptor for the morphogen FGF. It is categorized by a wide range of symptoms, including cranial deformations and syndactyly (fusion of digits). FGF is involved in the formation of the pharyngeal arches← (covered in the next chapter), which explains the craniofacial abnormalities. Relevant to this chapter is the ability of FGF (like many growth factors) to inhibit apoptosis←. Having a mutation that causes an FGF receptor to be on all the time inhibits apoptosis in the hand and foot paddles. Regions of apoptosis are required to produce fingers and toes, hence this mutation leads to syndactyly. Partial disturbances to FGF signals can lead to partial syndactyly, or webbing of the fingers or toes.
Otherwise there aren’t many mutations to apoptosis signal transduction cascade← genes that lead to congenital disorders. Does this mean apoptosis isn’t important to development? No, quite the opposite, it is essential. As a result, humans have redundancy when it comes to triggering apoptosis. We mentioned earlier that loss-of-function mutations require mutating both alleles for a physical change to occur, like only needing one of your two feet to operate the brakes on a car. Now imagine having 8 legs. Studing the roles of apoptosis in the development of mice shows that removing both alleles of the pro-death signal BAX has no effect, nor does removing both alleles of the pro-death signal BAK, but removing all 4 causes mice to die during the embryonic period after failing to form a functional nervous system and heart. Removing BOK, BAX and BAK is even more lethal (if you are wondering how something can be more lethal, here is further reading). The important concept here is that apoptosis is absolutely esential to development, and as a result human cells are really good at doing it. And people who study apoptosis must be very good at tongue-twisters.

"Michael Berryman, actor" by Stefan Borggraefe is licensed under CC BY 4.0Ectodermal Dysplasia (part 1 of 2)
Problems with the induction of neural crest cells during neurulation leads to disturbances in the formation of teeth, hair follicles, salivary glands and other structures. What these have in common is they are all specialized structures of the ectoderm, induced by neural crest cells to differentiate. In a healthy embryo, ectodermal cells receive morphogens which activate or inactivate the correct transcription factors to trigger differentiation into neural crest cells. Neural crest cells migrate to distant regions of the body, determine their location by interacting with morphogens in the ground substance←, and release other morphogens to induce regions of ectoderm to differentiate into sweat glands, salivary glands, tooth buds or hair follicles. Disruption of this process leads to a condition named Ectodermal Dysplasia.
This group of syndromes is rare, with only 7,000 cases worldwide, but there are at least 40 different genes implicated. Compare that to Sickle Cell Disease, which currently affects over 100,000 Americans (predominantly African Americans, Hispanic Americans, Greek Americans, Turkish Americans and Italian Americans), all due to mutations in a single gene, Hemoglobin-Beta. The point of this comparison is to highlight when these genes are expressed. The induction of ectodermal stem cells to proliferate and differentiate into different appendages is complex and occurs during embryogenesis. Mutation in the morphogens, the morphogen receptors, the second messengers or transcription factors and downstream genes that are activated to induce differentiation are all possible targets that cause Ectodermal Dysplasia. Mutations in these genes in a neural crest cell leads to a disruption in any of the subsequent cells induced by this new cell type, similar to the way tackling the ball carrier in soccer (football) disrups the gameplay of any of his or her potential passing targets. By comparison, only red blood cells express hemoglobin-beta, and since they are terminally differentiated cells, they do not become any other cell type. Obviously red blood cells are an important cell type, one that develops early in embryogenesis, but the symptoms of Sickle Cell Disease present less of a spectrum than the types of diseases we have been discussing, such as Ectodermal Dysplasia.
We discuss Ectodermal Dysplasia further in Chapter 8 as we cover tooth eruption←.

"Gaten John Matarazzo III" by Gage Skidmore, is licensed CC BY SA 3.0Cleido-cranial Dysostosis
Cleido-cranial dysostosis (CCD) is a congenital disorder caused by a mutation to a transcription factor required for the differentiation of bone and teeth. It is required to trigger osteo-chondro-progenitor cells to exit the cell cycle and differentiate into osteoblasts. It is also re-used to induce the differentiation of odontoblasts. Furthermore, after teeth have formed, this transcription factor is re-used to activate the expression of a matrix metalloproteinase enzymes necessary for remodeling of the alveolar sockets. Without this enzyme, retention of deciduous teeth occurs. Dental implants or dentures (such as the ones the actor and CCD-philanthropist Gaten John Matarazzo III received in Fig. 6.36) are the preferred treatment. In addition, a person with CCD may have small clavicles and changes to shape of the skull– those are bones that form by intra-membranous ossification. This illustrates two major concepts in development. First, many structures form one way, but are remodeled later to serve a different function (teeth form by folding inwards, they later move outwards). Secondly, many different patterns in embryology are re-used (recapitulated), such as the removal of tissue during neural crest cell migration or the removal of tissue during tooth eruption←.
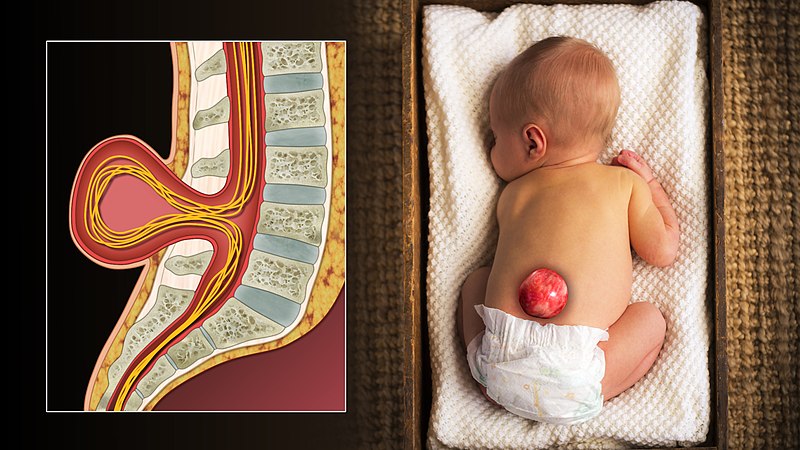
"3D Medical Animation still shot of Spina bifida in an infant" by scientific animations is licensed under CC BY-SA 4.0Spina bifida
Incomplete closure of the neural tube, or spina bifida, can result from a lack of adequate levels of folate during pregnancy. There are other less-common risk factors, such as taking certain anti-siezure medications or poorly managing diabetes during pregnancy. Folic acid is used in a wide variety of biological processes, but it is believed its role in methylation of DNA during differentiation is most important in spina bifida. Because neurulation occurs so early in development (week 4), waiting until a woman knows she is pregnant to prescribe folic acid supplements is often too late to be effective. Prescribing supplements to women who beleive they could get pregnant is better, or supplementing common foodstuffs like flour is even more effective for a populace as a whole.
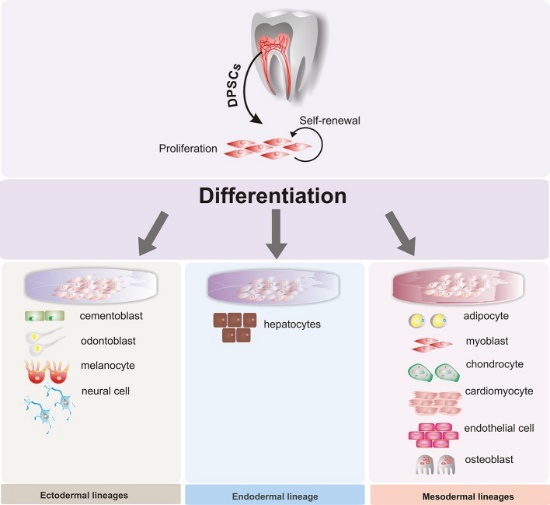
Figure 3” by Beatriz A. Ro Isdas-Junco et al, is licensed CC BY 3.0Stem cell therapies
When cells terminally differentiate, they permanently inactivate un-needed genes by methylation and storage around histones. Researchers are learning ways to reverse this process, and guide differentiated cells to revert to a stem-cell← state. This raises the possibility of promoting regeneration of tissues that do not otherwise regenerate, removing the need for tissue grafting or transplantation. Because some dental tissues do not regenerate well, there is potential for these technologies to be applied to the oral cavity, such as growing biological dental implants instead of using metals and ceramics. However, more interest has been placed on acquiring mesenchymal stem cells from dental tissues. For instance, stem cells isolated from maxillary third molars have been used in clinical trials to improve healing and reduce the need for transplanted tissue in maxillofacial surgery. Because of their potential to differentiate into a wide array of cells, great interest has been placed on collecting dental stem cells to treat diseases unrelated to the oral cavity. With the correct morphogens and plenty of dental stem cells, it may be possible to reverse the damage caused by disease such as Alzheimer’s Disease (AD) and Parkinson’s Disease (PD), spinal trauma, myocardial infarction (heart attack), and Muscular Dystrophy (MD). The lineage of the cells that produce dentin, pulp, cementum and the periodontium helps explain the link from teeth to neurodegenerative disoders. What else will you do with those extracted third molars?
< Chapter 5 * navigation * Chapter 7 >
Chapter review questions
The process by which animals and plants grow and change.
The branch of biology and medicine concerned with the study of embryos and their development.
Without shape
Slowly change shape
A period of three months, especially as a division of the duration of pregnancy.
A human offspring during the period from approximately the second to the eighth week after fertilization.
An unborn human baby more than eight weeks after conception.
The type or types of cell(s) a stem cell can possibly differentiate into in the future, determined by which genes are methylated and stored around histones, or free to be transcribed.
A medical condition that is present at or before birth, which can be acquired during development or from the genetic make up of the parents.
Agents or factors which cause malformation of an embryo.
Undifferentiated or partially differentiated cells that can differentiate into various cell types, and proliferate to produce more of the same stem cell.
The process of cell division, where one cell divides into two identical clones (daughter cells).
When a cell has finished its last possible differentiation step and lost the ability to undergo mitosis.
The developmental history of a differentiated cell traced back to the embryonic cell from which it arises.
A temporary group of cells that arise from the embryonic ectoderm, and in turn give rise to a diverse cell lineage—including melanocytes, cranio-facial cartilage and bone, teeth and periodontal tissue, smooth muscle, peripheral and enteric neurons and glia.
The mechanism by which initially equivalent cells in a developing tissue in an embryo assume complex forms and functions.
deoxyribonucleic acid is the hereditary material in humans and almost all other organisms.
When one cell begins to look different from another. This process involves limiting cell fate by altering gene transcription to become more specialized.
Copying DNA into a functional product, such as a RNA and/or protein. Controlled by the activity of transcription factors binding to gene promoter regions to recruit RNA polymerase.
A sequence of nucleotides in DNA that encodes the synthesis of a gene product, either RNA or protein.
A protein that controls the rate of transcription of DNA to mRNA, by binding to a specific DNA sequence.
When a chemical or physical signal is transmitted through a cell as a series of molecular events, most commonly protein phosphorylation catalyzed by protein kinases, which ultimately results in a cellular response.
Methyl groups added to DNA which change the activity of a gene without changing the sequence, typically repressing gene transcription.
Highly basic proteins found in nuclei that compact DNA into a denser form, unavailable for gene transcription.
The process of converting DNA into an mRNA copy
In the phrase nature vs nurture, nature refers to genetics (heritable traits).
In the phrase nature vs nurture, nurture means environmental factors that occur after fertilization, not DNA inherited from our parents.
The embryonic process in which one group of cells directs the development of another group of cells.
A substance whose non-uniform distribution governs the pattern of tissue development and pattern formation.
A signaling molecule capable of stimulating cell proliferation, wound healing, and cellular differentiation.
Signaling molecules secreted directly into the blood which travel throughout the body.
A cell-surface, trans-membrane or cytoplasmic protein that binds to (receives) a signaling molecule and transmit the signal further.
Heritable DNA modifications that do not change the DNA sequence but do affect gene activity.
The shape (or form) of.
Bone Morphogenetic Proteins are a group of signaling molecules, initially discovered for their ability to induce bone formation, now known to play crucial roles in all organ systems.
Signaling molecules first identified for their role in carcinogenesis, then for their function in embryonic development, including body axis patterning, cell fate specification, cell proliferation and cell migration.
Fibroblast Growth Factors are a family of morphogens involved in a wide variety of processes, including important roles in development and tissue regeneration, especially connective tissues.
Gel-like substances in the ECM, composed of water held in place by large molecules (proteins, glycoproteins and glycosaminoglycans).
In pattern formation, the development of spatial organization in the embryo that results from cells differentiating at specific positions, which requires that the cells have positional values as in a coordinate system
A group of 235-300 related genes that code for a transcription factors, which control the activity of other genes involved in development, including directing the formation of limbs and organs along the anterior-posterior axis.
A biological structure or chemical agent that interferes with the physiological action of another.
The process that results in an increase of the number of cells, and is defined by the balance between cell divisions and cell loss through cell death or differentiation.
Extra-Cellular Matrix: Materials in the body, but outside of cells. A network of macromolecules, such as fibers, enzymes, and glycoproteins, that provide structural and biochemical support to surrounding cells.
The increase in diameter by the addition of tissue at the surface,
Increase in size by the addition of tissue from the inside.
A hard connective tissue which is mostly ECM, including collagen fibers and a calcium-phosphate crystal.
An embryonic tissue composed of undifferentiated mesenchymal stem cells and mucous ground substance.
Trans-membrane structure specialized for cell-to-cell adhesion.
Cell Adhesion Molecules: proteins located on the cell surface involved in binding with other cells or with the extracellular matrix.
A type of cell-to-cell contact that prevents diffusion between cells.
Outward-folding of an epithelium caused by interstitial growth.
Inward folding of an epithelium caused by interstitial growth.
The top (or apex) side of a cell or tissue, usually facing the lumen.
The side of a cell or tissue oriented away from the lumen or external surface.
Epithelium on the inner wall of the gingiva that attaches to connective tissue of the lamina propria on the basolateral side and to the surface of the tooth on the apical side.
Top-to-bottom polarity, where the apical side of a cell (or tissue) is different from the basolateral side
The biological process that causes a cell, tissue or organism to develop its shape.
An opening or split in the roof of the mouth that occurs when the palatal shelves and/or primary palate fail to fuse completely.
A phase early in the embryonic development during which the single-layered blastula is reorganized into a multilayered structure known as the gastrula.
An orange-to-yellow pigment made by plants that accumulates within the dermis of the skin. It is the precursor for Vitmain-A.
A type of mutation in which the altered gene product possesses a new molecular function or a new pattern of gene expression. Gain-of-function mutations are almost always Dominant.
a variant or different DNA sequence of a gene
A mutation that result in the gene product having less or no function (being partially or wholly inactivated).
The continued development of a cell, tissue, organ or organism as it takes on a more adult form.
To state again, or to repeat.
When two or more cells, tissues or organs join to become one.
A trans-membrane protein which allows cells to bind to the ECM protein fibronectin, it is involved in cell adhesion, growth, migration, and differentiation.
A large glycoprotein found in the ECM which binds to integrin proteins on the cell surface, involved in cell adhesion, growth, migration, and differentiation.
Signaling molecules which control the navigation of other cells by causing attraction or repulsion.
Direct contact between cells allows the receptors on one cell to bind small molecules on the plasma membrane of different cell. In eukaryotes, many of the cells during early development communicate through direct contact.
Programmed cell death
The reversal of differentiation, reverting to a more stem cell-like state.
A process by which epithelial cells lose polarity and cell-cell adhesion, and gain migratory and invasive properties to become mesenchymal stem cells, this normally occurs during embryonic development and wound healing.
A reversible process that involves the transition from motile mesenchymal cells to planar arrays of polarized epithelial cells.
Extracellular matrix material involved in the repair of injured and missing tissues, allows stem cells to migrate into the injured area. It is usually replaced during regeneration.
A firm connective tissue, softer and more flexible than bone composed of chondrocytes and lots of ground substance.
A differentiated connective tissue cell that secretes bone ECM, including collagen, calcium and phosphate.
A congenital malformation that may decrease the mobility of the tongue caused by an unusually short lingual frenulum.
The first two weeks of human development, starting with fertilization and ending with implantation of a morula.
The fusion of haploid gametes, egg and sperm, to form the diploid zygote.
DNA molecule packaged into thread-like structures found during mitosis, visible under a light microscope.
A diploid cell resulting from the fusion of two haploid gametes; a fertilized ovum.
the gelatinous material within a living cell, excluding organelles.
The process by which a developing embryo makes contact with the uterine wall, attaches and digests its way internally, and remains within it until birth.
Control proteins and enzymes which ensure proper progression through the cell cycle, regulating the rate of mitosis.
The most common chromosomal anomaly in humans, also known as Down syndrome, caused by an extra chromosome 21.
A condition in which one or more teeth appear smaller than normal
The first few cellular divisions of a zygote are synchronized and divide along longitudinal planes, the second division is at 90 degrees to the plane of the first, and the third is perpendicular to the first two.
A trans-membrane protein that when paired allows small cytoplasmic molecules to pass through from one cell to another cell.
A solid ball of cells that develops by mitosis from the single-cell zygote.
A hollow ball of cells that develops after the morula stage of embryogenesis.
The mass of cells inside the blastula-stage embryo that will eventually give rise to the definitive structures of the fetus
Cells that form the outer layer of a blastula which provide nutrients to the embryo and develop into a large part of the placenta.
Single-stranded RNA molecule complementary to one strand of DNA of a gene. It leaves the nucleus and moves to the cytoplasm where it instructs the synthesis of a protein.
The process of turning the sequence of a mRNA into a sequence of amino acids during protein synthesis
The three layers of cells that arise from gastrulation: endoderm, mesoderm and ectoderm.
he most exterior of the three primary germ layers formed in the gastrula, it gives rise to the epithelial tissue covering the body and the CNS.
The innermost of the body's 3 embryonic tissues that form during gastrulation, it becomes the inner lining of hollow organs.
The middle of the three embryonic layers that develop during gastrulaton, mesoderm becomes most of the body's muscle and connective tissues.
The organizer for gastrulation in the embryo, it is the site where mesoderm migration occurs.
The visible line that forms on the dorsal side of the embryo as Hensen's node travels in a rostral-to-caudal direction, creating the embryos left/right symmetry.
Multipotent cells of a connective tissue that can differentiate into a variety of cell types, including osteoblasts, fibroblasts, chondrocytes, myoblasts, blood cells and adipocytes.
The mucous membrane lining the inside of the mouth. It is a stratified squamous epithelium, named the oral epithelium, and an underlying areolar connective tissue named the lamina propria.
A terminally differentiated epithelial cell capable of synthesizing large amounts of the protein keratin within its cytoplasm.
The folding process in vertebrate embryos, which includes the transformation of ectoderm into the neural tube.
A flexible rod formed of a material similar to cartilage, which ultimately disappears in human (and most vertebrate) embryos.
Cells derived from ectoderm fated to develop into the CNS or neural crest.
The embryonic precursor to the central nervous system.
A group of red, dark brown or black pigments found in the hair, skin, and other places, capable of absorbing UV-B radiation.
Terminally differentiated cells derived from neural crest cells that produce one of the three forms of melanin.
A cell of neural crest origin that is part of the outer surface of the dental pulp, and whose biological function is the formation of dentin.
Differentiated cell that deposits cementum matrix.
Mesenchyme tissue that contains neural crest cell derivatives.
A series of externally visible anterior tissue bands lying under the early brain that give rise to the structures of the head and neck.
Arm-like extension of an odontoblast found within dentinal tubules.
Enzymes that degrade all kinds of extracellular matrix proteins, or process a number of bioactive molecules. They play a major role in cell proliferation, migration, differentiation, angiogenesis, and apoptosis.
Periodontal Ligament, a group of specialized connective tissue fibers that attach a tooth to alveolar bone.
A mass of tissue having the potentiality of differentiating into a tooth.
Bilateral pairs of blocks of mesoderm that form along the rostral-caudal axis.
Growth of endothelial cells, creating new blood vessels within a tissue.
The anterior end of the primitive gut tube, derived from yolk sac endoderm, not yet connected to the oral cavity.
Small bumps that give rise to bigger structures such as hair follicles and teeth.
An infolding of the epidermis that extends deep into the dermis, responsible for producing a hair.
A group of disorders in which two or more of the ectodermally derived structures — the skin, sweat glands, hair, nails, teeth and mucous membranes — develop abnormally.
A process in tooth development in which the teeth enter the mouth and become visible.
A rare congenital malformation that affects the collarbones, skull and teeth.
Formation of bone tissue from a dense connective tissue model
Reorganization or renovation of existing tissues, either physiological or pathological. The process can either change the characteristics of a tissue such as in blood vessel remodeling, or result in the dynamic equilibrium of a tissue such as in bone remodeling.
A congenital malformation involving incomplete closure of the neural tube.
After partial loss of as tissue, based on the remaining part, the tissue grows the same structure and function as the lost part.

