1.4 Summary Problems

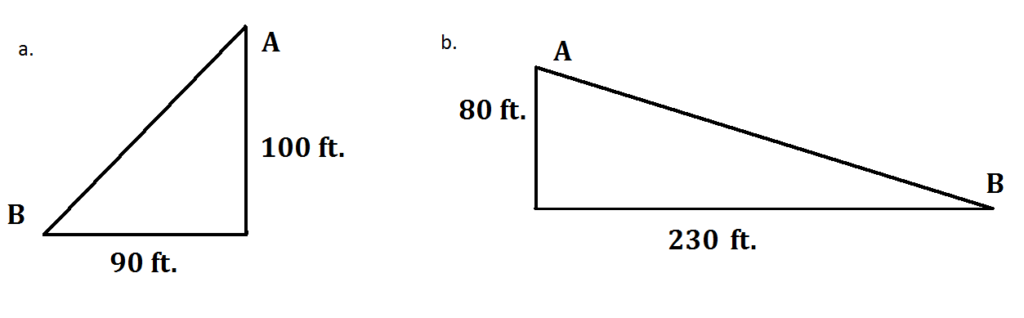
1. Using the measurements provided, determine the %slope of the following slopes between Points A and B.

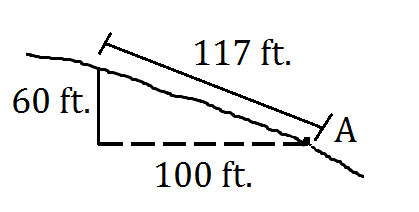
2. On a 60% slope, Todd wants to walk up a slope a distance equivalent to 100 feet horizontal distance. How far should he walk from Point A?

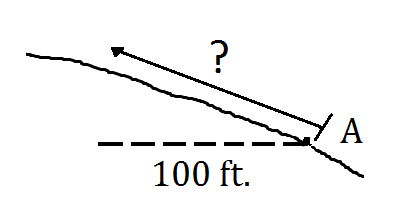
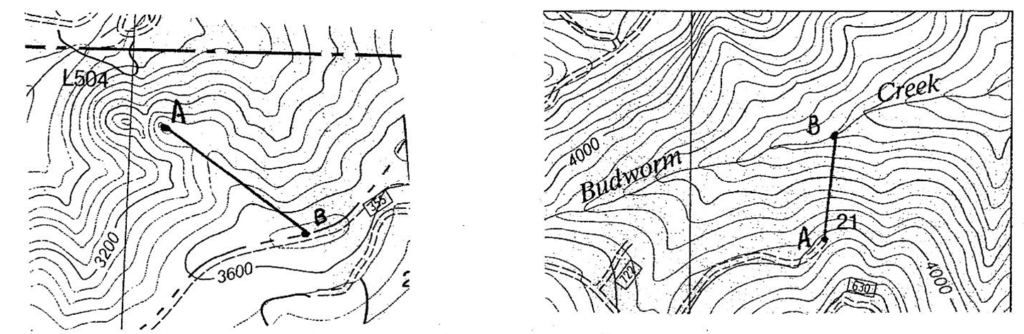
3. Determine the average slopes between Points A and B on the contour maps below. The scale is 1 inch=2000 feet.  The contour interval is 80 feet.

Answers to Summary Questions

1. [latex]\displaystyle \left( {\frac{{rise}}{{run}}} \right)\left( {100} \right)=[/latex]%slope

1a. [latex]\left( {\frac{{100ft}}{{90ft}}} \right)\left( {100} \right)=[/latex]111%

1b. [latex]\left( {\frac{{80ft}}{{230ft}}} \right)\left( {100} \right)=[/latex]35%

2.  On a 60% slope, we know that the rise is 60% of the run. Therefore, the rise here should be 60 percent of 100 feet or 60 feet.  Using the Pythagorean theorem, we can solve for the hypotenuse.

a² + b² = c²      where:

100² + 60² = c²

13,600 = c²       

[latex]\sqrt{{13,600}}=117[/latex]ft.

3. The answers to these questions will depend upon how you measured the horizontal, or map distance, which can be hard to do on a screen.  My measurements are shown on the maps below:

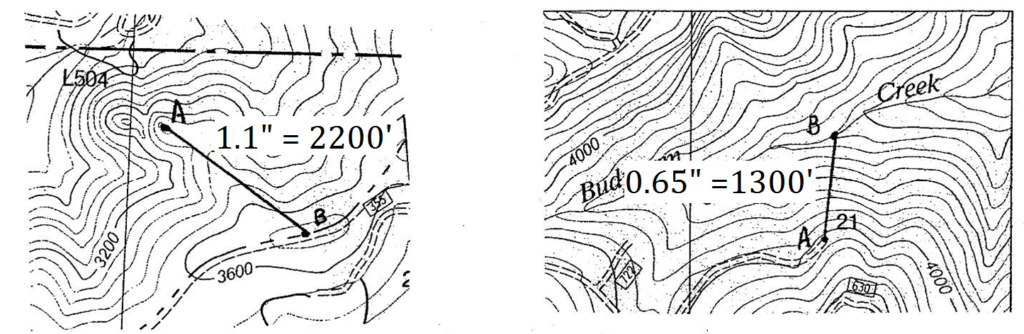
At left. Point A is ≈ 3440 feet.  Point B is ≈ 3720 feet.  The rise is 280 feet.  The run is ≈ 2200 feet.  Therefore, the average slope is (280)(100)/2200 = 13%.

At right.  Point A is ≈ 4040 feet.  Point B is ≈ 3280 feet.  The rise is 760 feet.  The run is 1300 feet.   Therefore, the average slope is (760)(100)/2200 = 58%