2.4 Using Topographic Slope to Determine Tree Height

For most natural resources management purposes in the United States, land areas and distances are measured in English units.  (Research data are collected in metric units.)  Therefore, we measure area in acres, tree height in feet, and commonly, horizontal distance in chains (1 chain = 66 ft.).  For this reason, many instruments for measuring slope have two scales:  %slope and topographic slope.  Topographic slope (or Tslope) is essentially the same as %slope, except that instead of expressing the ratio of rise over run as a proportion of 1:100, Tslope is expressed in a proportion of 1:66 as follows:

[latex]\left( {\frac{{\text{rise}}}{{\text{run}}}} \right)\left( {66} \right)[/latex] = Tslope

The different multiplier (66) is the only difference between Tslope and %slope. To solve the Tslope equation for rise we do the following:

1. Multiply both sides of the equation by run to cancel out run on the left side of the equation

[latex]\displaystyle \frac{{\left( {run} \right)\left( {rise} \right)\left( {66} \right)}}{{run}}=[/latex](run)(Tslope)

2. Divide both sides by 66 to cancel out 66 on the left side of the equation

[latex]\displaystyle ~\frac{{\left( {rise} \right)\left( {66} \right)}}{{66}}=\frac{{\left( {run} \right)}}{{66}}[/latex](Tslope)

That leaves the following equation:

[latex]\displaystyle rise=\frac{{\left( {run} \right)}}{{66}}[/latex](Tslope)     where rise =height

So, just as with %slope, the Tslope multiplier (66) becomes the denominator.

Topographic slope is most commonly used when measuring merchantable height, but it is also fine for measuring total height on shorter trees. Here is an example (Figure 2.8):

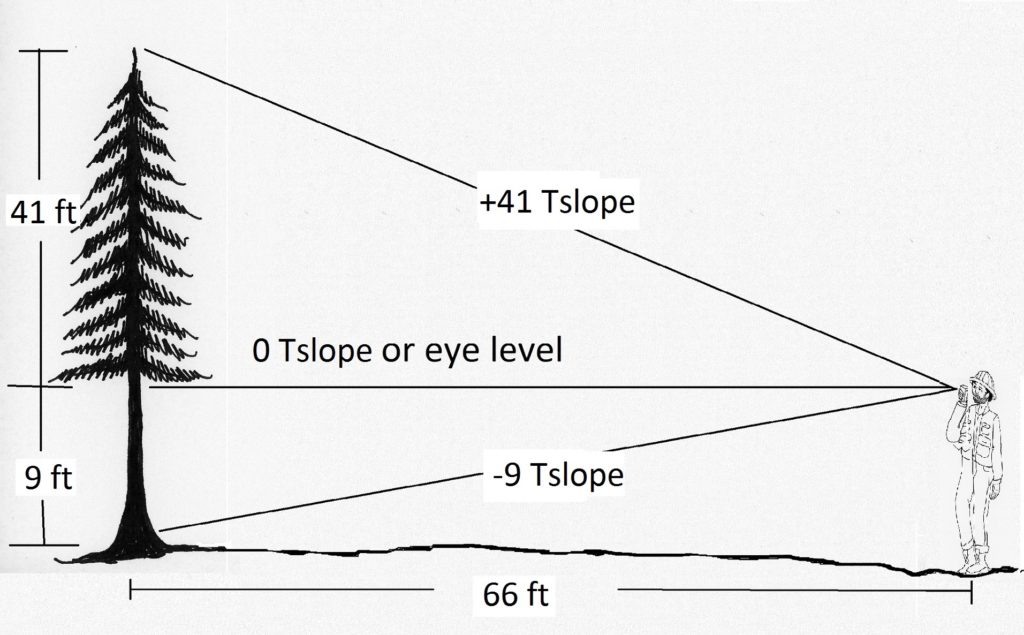
[latex]\displaystyle rise=\frac{{\left( {run} \right)}}{{66}}[/latex](Tslope)

[latex]\displaystyle rise=\frac{{\left( {66} \right)}}{{66}}[/latex](41+9)

rise (height) = 50 feet.