2.5 Measuring Height on Irregular Trees
Species considerations: It is quite easy to measure tree height on conifers because conifers have a very distinct top. Each year’s whorl of growth produces a clear tip with short lateral branches, even on hemlocks (Tsuga spp.; tree on the right in Figure 2.9).


Hardwoods on the other hand, have rounded crowns that are often a function of the amount of sun they are able to capture (Figure 2.10). Under shaded conditions, they may be very one-sided. Therefore, it is extremely important to get a clear view of the whole crown, so that side branches are not mistaken for the top.
Broken tops: Trees in which the top has blown out can be tricky. The short or nonexistent tip is often hidden by long lateral branches near the top of a tree. If the top cannot be seen clearly, it is easy to mistake the tips of the lateral branches for the top. A rounded or flat top in a conifer suggests a missing top, and this type of tree should always be examined closely (Figure 2.11). As seen previously in Figure 2.7, measuring a lateral branch instead of the tip can overestimate the tree’s height. The closer one is to the tree, the greater the error. This is another reason why it is important to walk a distance far enough from the tree to get a clear view of the top.

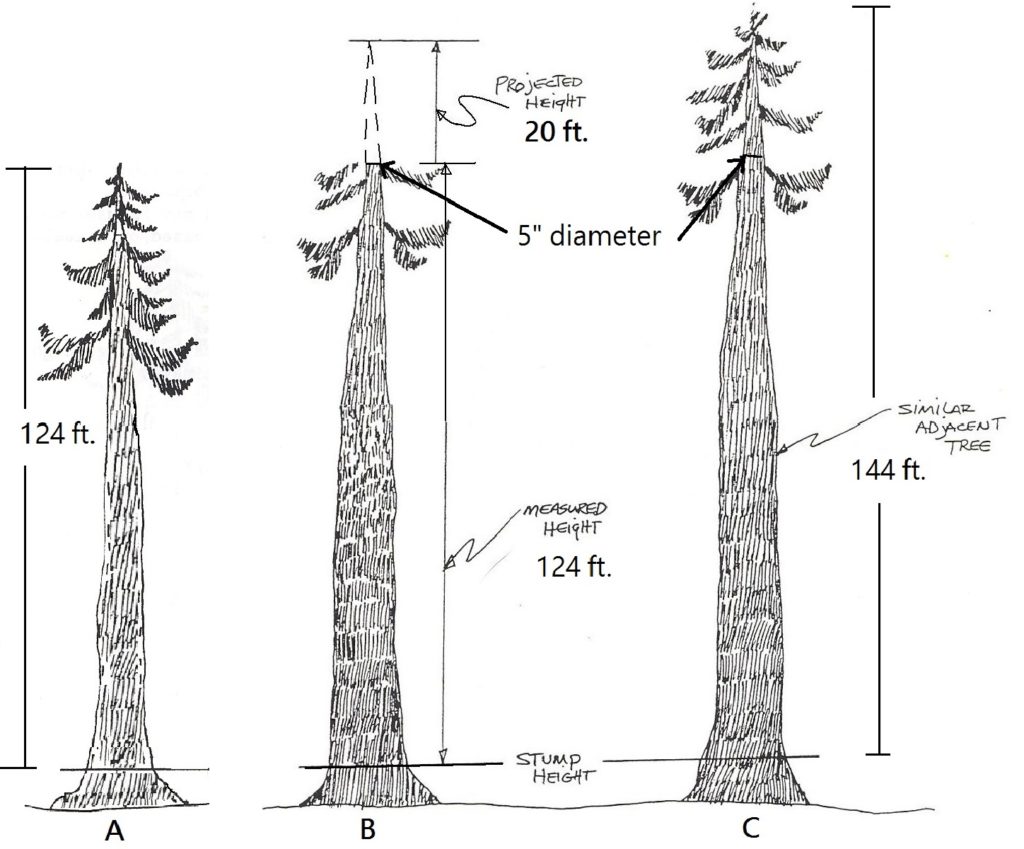
When measuring total height on trees with broken tops, the tree top must be “reconstructed” in order to maintain a tree’s correct taper, or “original” shape. Incorrect taper will affect wood volume estimates. A normal tree that is 124 feet tall (A below) has a very different shape than a tree whose top has broken out at 124 feet (B below). The standard method for reconstructing a tree’s top is to look at the surrounding trees and estimate the broken tree’s missing height from their growth. Let’s say a tree similar in diameter and taper to the broken-top tree (C below), extends 20 feet from a diameter of five inches to its tip (Figure 2.12). Using this as a guide, one could add 20 feet to the broken-top tree for a reconstructed total height of 144 feet. (This missing wood would then be subtracted to determine the tree’s net volume.)
Leaning trees: For leaning trees, it is necessary to adjust the image of the tree-to-ground triangle. In this case, the leaning tree is the hypotenuse of the triangle instead of the rise (Figure 2.13). The height of the tree can be estimated using the Pythagorean theorem and the following steps:
1. Measure out a horizontal distance from the tip of the tree until it is clearly in view.
2. Calculate the perpendicular distance from the tip of the tree to the ground (rise), using %slope readings as before.
3. Measure the horizontal distance from the perpendicular drop to the base of the tree (the run).
4. Once these two sides of the triangle have been determined, estimate the total tree height using the Pythagorean theorem to solve for the hypotenuse.
See the example in Figure 2.13 below:
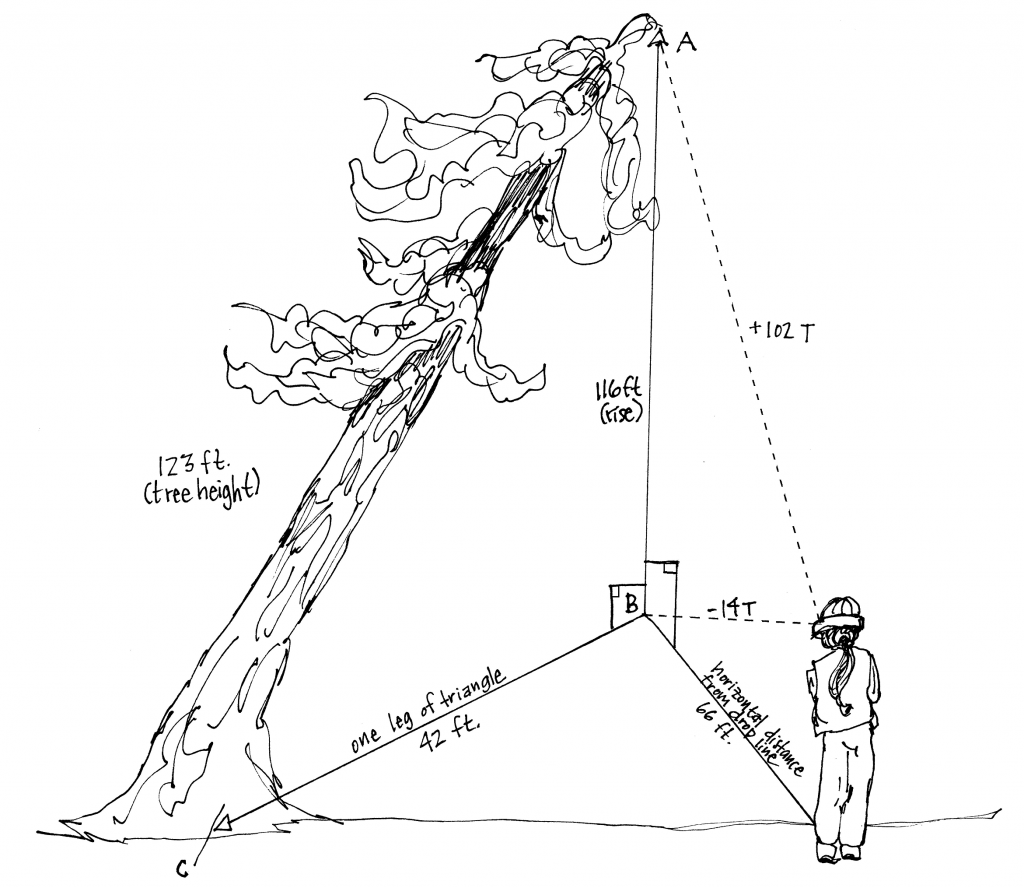
1. The technician walks out a horizontal distance from fall line AB; in this case 66 feet.
2. A Tslope reading is taken to the tip of the tree (A) (+102T), and then to the point on the ground where the AB fall line intersects the ground (B) (-14T). Using the two T slope readings, the rise of the triangle (line AB) is determined; in this case, 116 feet.
3. The horizontal distance between Point B and the stump of the tree (C) is measured with a tape to determine the run; in this case 42 feet.
4. Finally, using the Pythagorean theorem, the hypotenuse or height of the tree can be determined.
[latex]{{\text{c}}^{2}}={{\text{a}}^{2}}+{{\text{b}}^{2}}[/latex]
or
[latex]\text{c}=\sqrt{{{{\text{a}}^{2}}+{{\text{b}}^{2}}}}[/latex]
so
[latex]\text{c}=\sqrt{{{{{116}}^{2}}+{{{42}}^{2}}}}[/latex]
and
[latex]\text{c}=\sqrt{{{{{15220}}^{{}}}}}[/latex]
c = 123 feet.
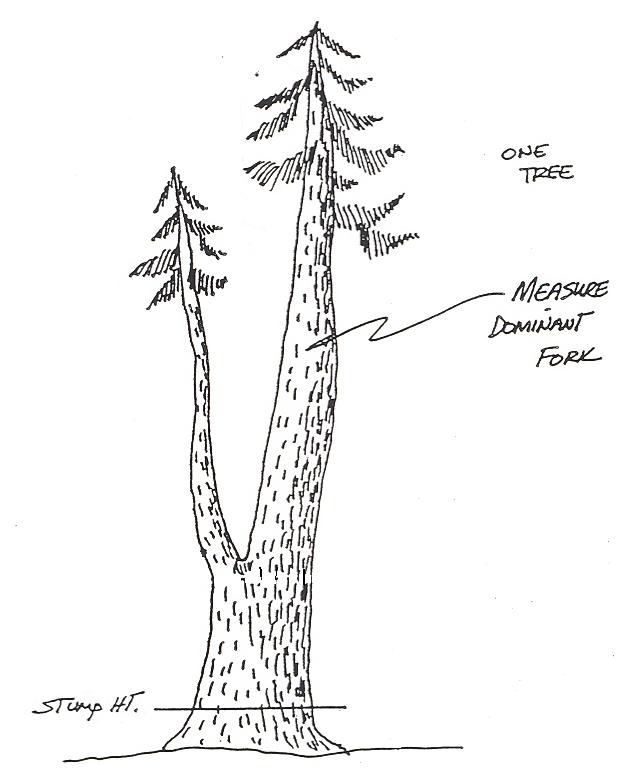
Forked Trees: On forked trees, the tallest, or dominant fork is measured (Figure 2.14). In some cases, the second fork occurs low enough in the tree to be counted as a second tree, but for most trees, the tallest fork is the only merchantable fork.

