2.7 Field Technique Tips for Measuring Tree Height

Estimating total tree height is very easy to do correctly, but does require some thought about how the measurements are taken.  Here are some tips.

1. Always walk to where one can clearly see the tree top. This can be tough to do, especially in dense stands, on extremely foggy days, or in stands with heavy brush. Dragging a tape around in brush trying to get to that special spot where the tree tip comes into view can be frustrating, but it needs to be done. It is actually pretty rare to have a tree whose crown is impossible to see somewhere within 150 feet. This is why it is important to remain flexible in selecting horizontal distances.  Commonly, errors in measuring tree height come from measuring a branch instead of the tip, measuring the wrong tree top, or guessing where the tree top is in a dense canopy.

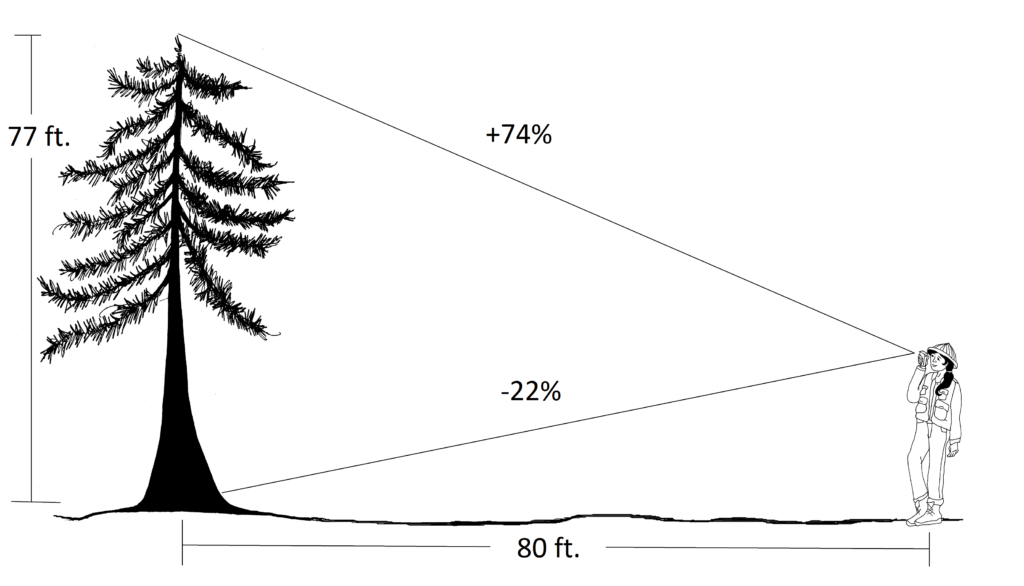
2. Do not always rely on that magical distance of 100 feet (Figure 2.16).  Once you get comfortable with the instruments in the field, find a method that allows you to be flexible in choosing your horizontal distance from a tree.  Discover a fast way to adjust your heights with varying horizontal distances. Some people have to follow a formula. If you don’t want to mess with the formula, just think of 66 (for Tslope) and 100 (for %slope) as “calibrating” distances.   For example:

• Tslope:  A horizontal distance of 33 feet from a tree is one half of the calibrating distance of 66 feet from the tree, so tree height is half of the combined Tslope readings.
• Percent slope: Likewise, 50 feet is 50 percent of 100; so a tree height measured from a horizontal distance of 50 feet is 50 percent of the slope readings. At 90 feet, the tree height is 90 percent of the slope readings, etc.
• A technician measures a tree, getting +74% to the top, and –22% to the stump. 74+22 = 98. At 60 feet from the tree (60% of 100), the tree height is 60 percent of 90 or 54 feet. At 80 feet from the tree (80% of 100), the tree height is 80 percent of 90 or 72 feet. At 120 feet from the tree (120% of 100), the tree height is 120 percent of 90 or 108 feet.

3. When the canopy is very dense, it may be difficult to discern which top belongs to the tree you are trying to measure. A partner can push repeatedly on the tree trunk at shoulder height. The force will reverberate up the trunk and make the tip wiggle, so you can pick out your tree among the other crowns.

4. A good rule of thumb is to walk out a distance that is approximately equal to the tree’s height. One should not try to measure 130-foot trees from a distance of 50 feet.

5. When determining height, always record measurements to the precision of your instrument. When holding any instrument to your eye, it is extremely difficult to hold it steady enough to measure between marks. Therefore, heights are always recorded to the nearest foot. Even though a calculator or laser may report distances and heights to one or two decimal places, the actual precision is not that great due to arm and head movements during measurement.

6. Make sure your run measurement is a horizontal distance, not a slope distance.   An incorrect run can result in an incorrect height estimate (Figure 2.17).

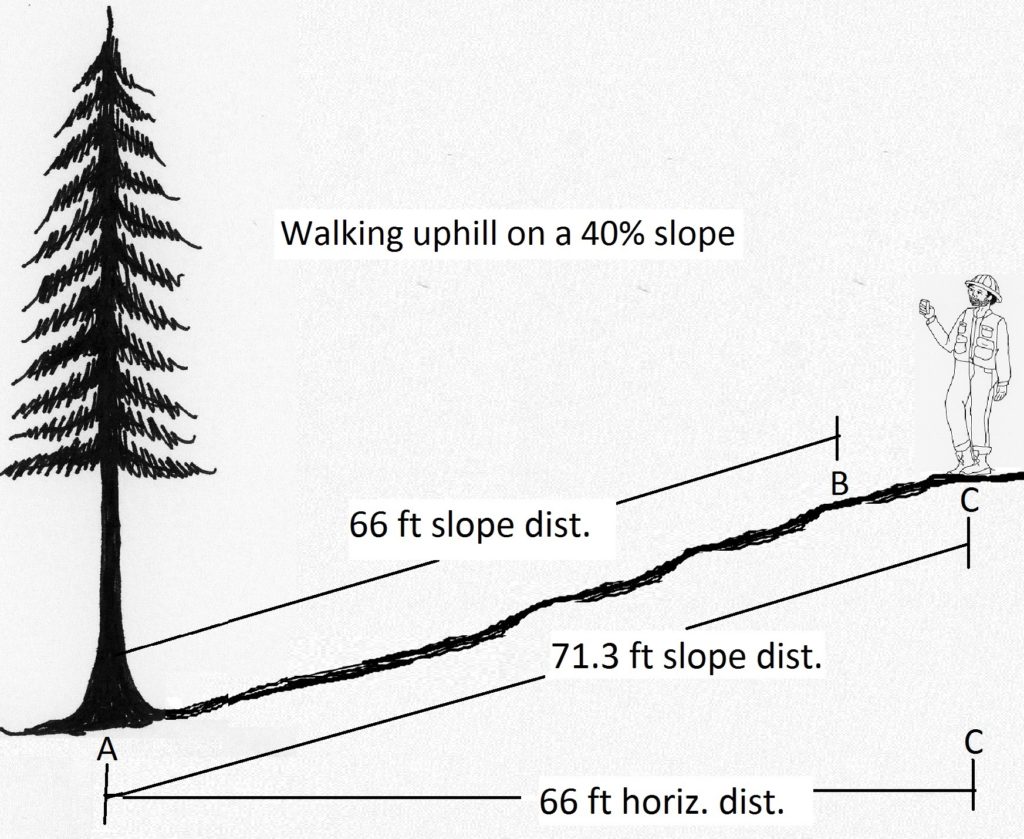
7. On slopes, walk out from the tree along the contour. Do not walk upslope and especially do not walk downslope (Figure 2.18). Walking downhill will put you beneath the tree and make the angle to the tree top even more obscure.

8. In a pinch, it may be necessary to walk either uphill from the tree or downhill from the tree. In these cases, the horizontal distance must be determined, either by using trigonometry, the Pythagorean theorem, slope distance conversion charts, or a laser rangefinder (Figure 2.17). Also note that if you measure from a place where the stump is below eye level, the bottom slope reading is subtracted from the top reading as explained in Figure 2.19.

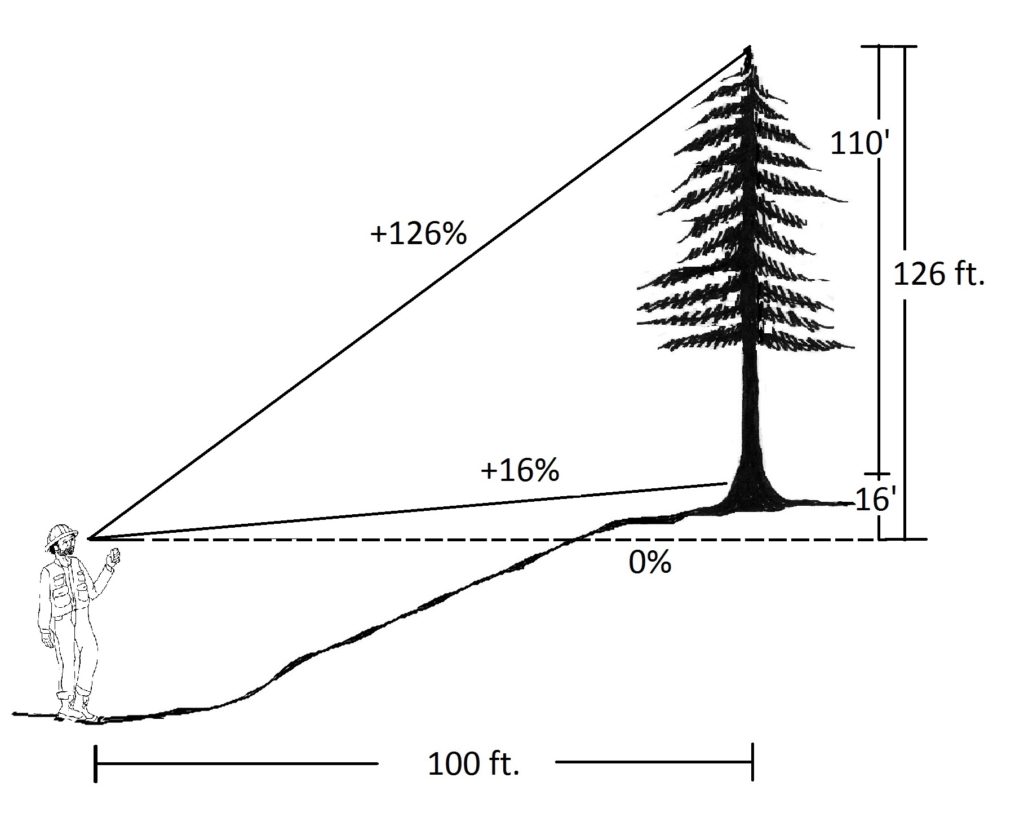
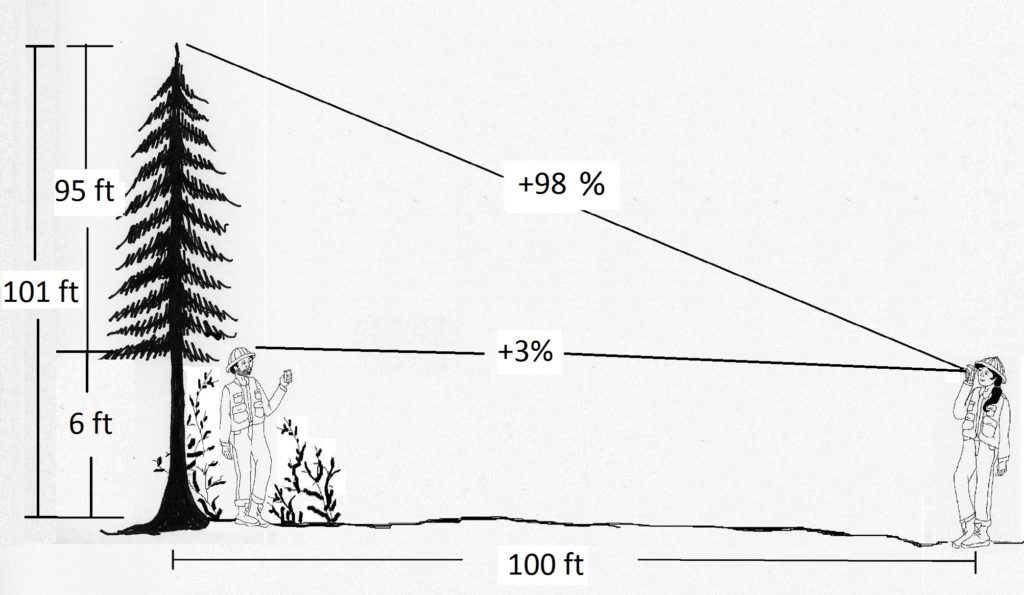
9. In situations with very thick brush, it may be impossible to see the stump of the tree. In this case, sighting on a partner’s hard hat or some other target, and adding in that height at the end, will result in a more accurate tree height as shown in Figure 2.20 below. The technician sights to the top of the tree and reads +98%. She then sights to the top of her partner’s hardhat and reads +3%.  Since both readings were taken while looking uphill, the second reading is subtracted from the first to obtain the tree height above the hat.  At 100 feet horizontal distance, 98%-3% =95 feet.  The height from the stump to her partner’s hardhat is then added, or 6 feet, for a total of 101 feet.