2.8 Summary Questions

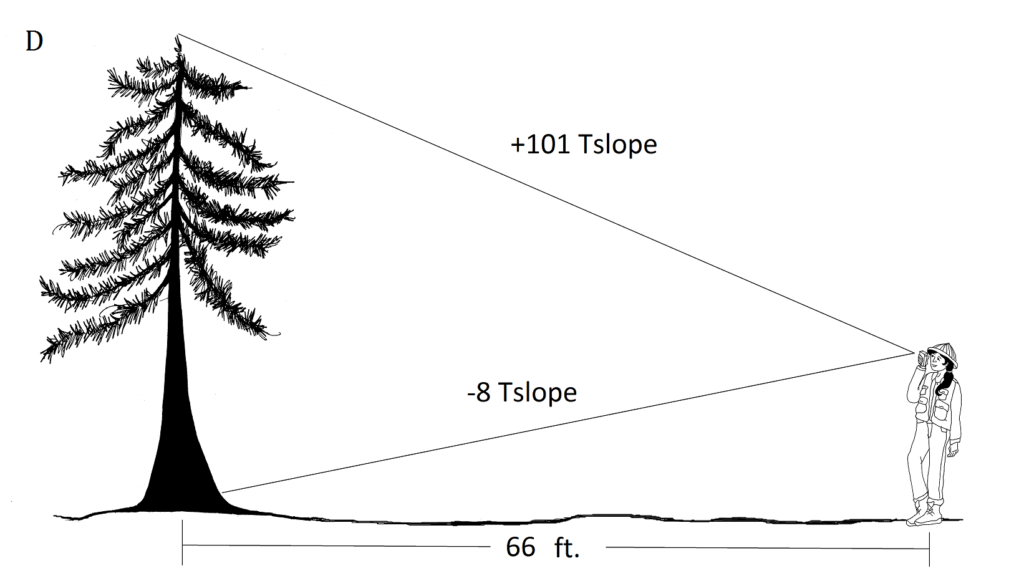
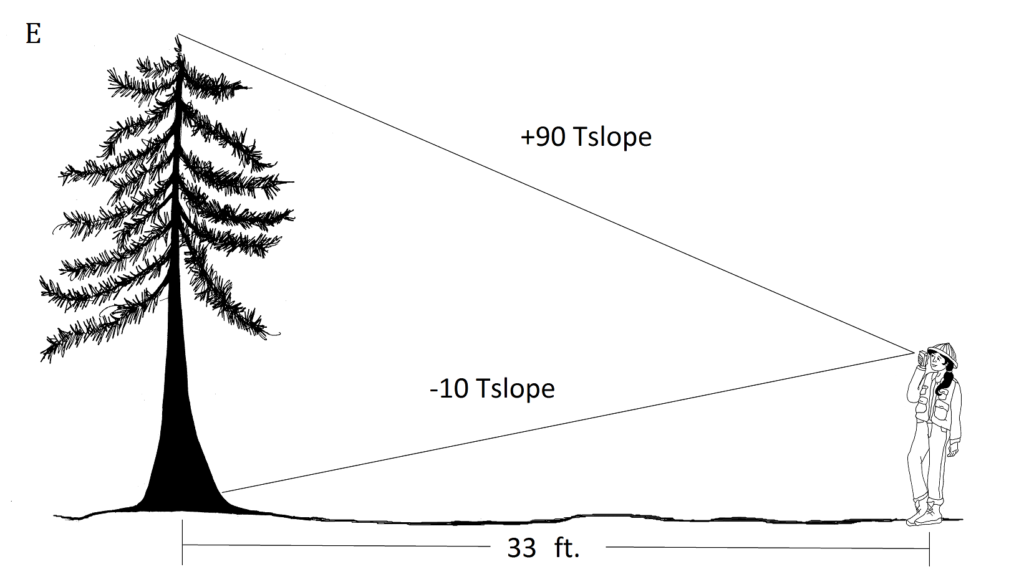
1. Determine the total heights of the trees illustrated below. Pay attention to the horizontal distances and slope scale used for each.

2. How should the total height of this flat-topped tree be determined?

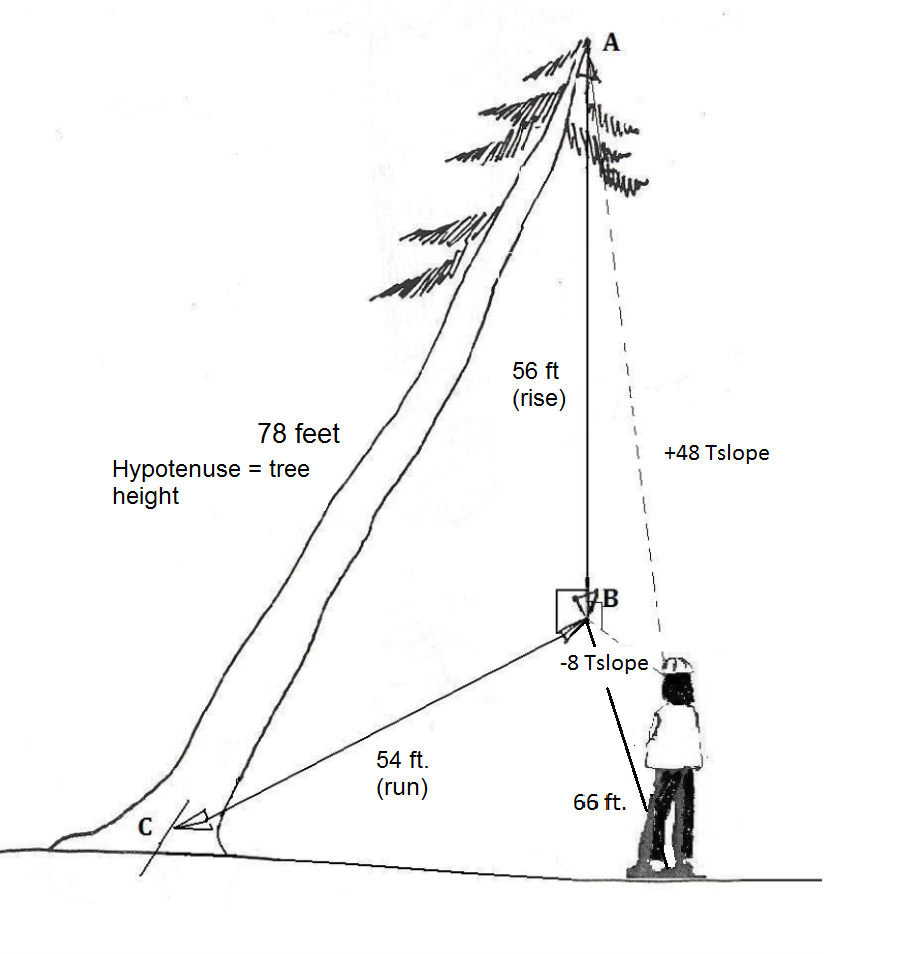
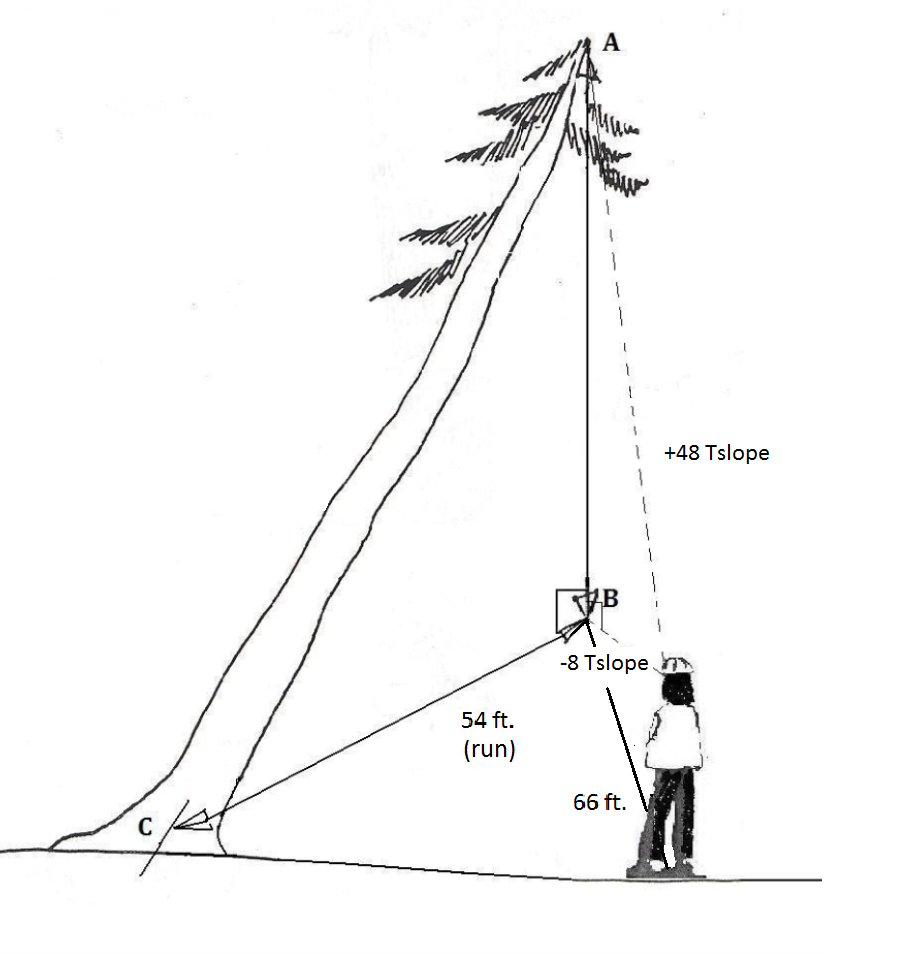
3. Calculate the height of the leaning tree.

Answers to Summary Questions

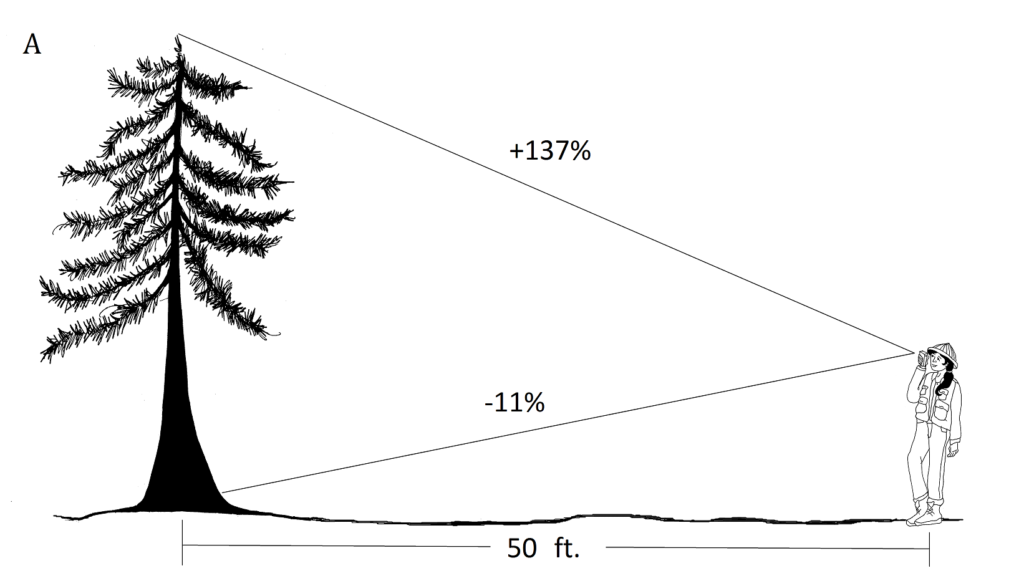
1. A. [latex]\displaystyle rise=\frac{{\left( {run} \right)}}{{100}}[/latex](%slope)

[latex]\displaystyle rise=\frac{{\left( {50} \right)}}{{100}}[/latex](137+11)

rise (height)= 74 feet

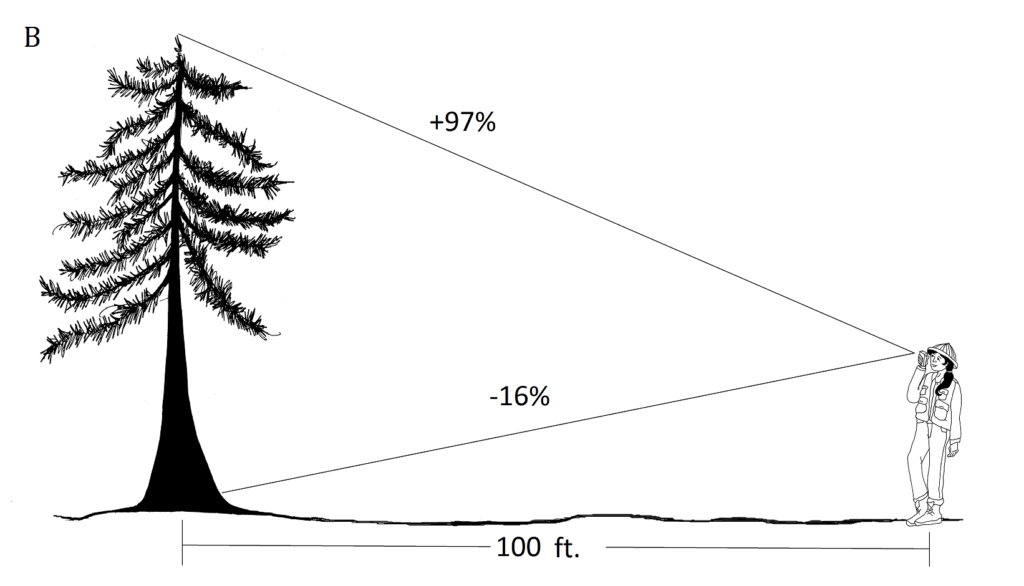
I.B. [latex]\displaystyle rise=\frac{{\left( {100} \right)}}{{100}}[/latex](97+16)

= 113 feet

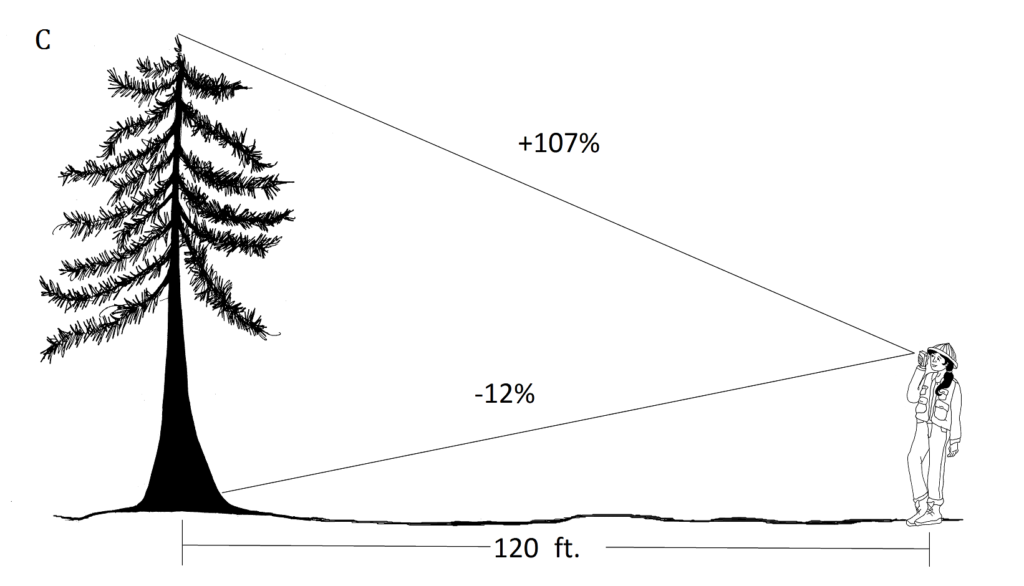
I.C. [latex]\displaystyle rise=\frac{{\left( {120} \right)}}{{100}}[/latex](107+12)

= 143 feet

I.D. [latex]\displaystyle rise=\frac{{\left( {run} \right)}}{{66}}[/latex](Tslope)

[latex]\displaystyle rise=\frac{{\left( {66} \right)}}{{66}}[/latex](101+8)

rise (height) =  109 feet

I.E. [latex]\displaystyle rise=\frac{{\left( {33} \right)}}{{66}}[/latex](90+10)

=  50 feet

2. The top of the tree will have to be reconstructed because of the broken top. This can be done by using a neighboring tree similar in size and taper as a reference.

3. a. The rise of the fall line from  the top of the tree to the ground = [latex]\displaystyle rise=\frac{{\left( {run} \right)}}{{66}}[/latex](Tslope)

[latex]\displaystyle rise=\frac{{\left( {run} \right)}}{{66}}[/latex](48+8)

=  56 feet

b.  The horizontal distance from the base of the tree to the fall line is 54 feet.  Thus you have two sides of the right triangle.

Using the Pythagorean theorem to determine the tree length (hypotenuse):

a² + b² = c²      where:

56² + 54² = c²

6052 = c²       

[latex]\sqrt{{6052}}=[/latex] 78 feet