
Life is astoundingly diverse. It is not a straightforward exercise to count species, but carefully produced estimates do exist. One such estimate predicts approximately 8.7 million species exist globally, about 2.2 million of which are marine[1]. Huge numbers of species, which likely include the vast majority of all that exist, have yet to be described.
These organisms, representing the three great domains Eukarya, Bacteria and Archaea occupy every environmental niche imaginable, from the human gut to the frozen expanses of the Antarctic, and from the rainforests of the Amazon basin to the acid waste washes of gold mines. Some organisms, like the tardigrades (Figure 1.1), or water bears, can withstand incredibly harsh conditions – from a few degrees above absolute zero to 300°F, the vacuum of outer space, and pressures greater than those at the greatest depths of the ocean. In the memorable words of Dr. Ian Malcolm in the movie, Jurassic Park, “Life finds a way”.
Despite the differing demands of existence in these widely varied environments, all living things share some common characteristics. The most noticeable of these is that from hummingbirds to humpback whales, from fungi to frogs, and from bacteria to birch trees, all living things are made up of cells. This fact was first discovered by Robert Hooke, in 1665 (Figure 1.2), when he used a microscope to look at a slice of cork and found that it seemed to be made up of tiny chambers that he named cells. Subsequent examination of other living things revealed that they too were, without exception, made up of cells. Today, we know that organisms in all three domains of life share this property – they are all made up of cells. For some, a single cell is the entire organism, while others are multicellular, like humans, wombats or weeping willows.

Figure 1.1 – Tardigrade Wikipedia
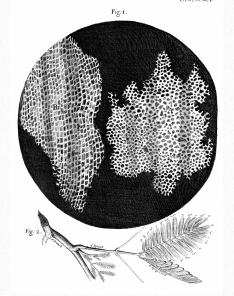
Figure 1.2 Slices of cork as seen by Hooke
The subject of this book is biochemistry, the science that explains life at the molecular level. The special characteristics of cells influence the unique chemistry of life. It is, thus fitting to take a look at cells, the setting in which the molecular events of life take place.
Figure 1.3 Bacterial cells Wikipedia Figure
“There are living systems; there is no “living matter”. No substance, no single molecule, extracted and isolated from a living being possess, of its own, the aforementioned paradoxical properties. They are present in living systems, only; that is to say, nowhere below the level of the cell.” – Jacques Monod
Cells
All cells, no matter what kind, have a plasma membrane that serves as a boundary for the cell, separating it from its surroundings. They also possess a genome made up of DNA that encodes the information for making the proteins required by the cell. To translate the information in the DNA and make the proteins it encodes, all cells have the machinery for protein synthesis, which include the structures named ribosomes and tRNAs. DNA is also the repository of information that gets copied and transmitted to the next generation, allowing living cells to reproduce.
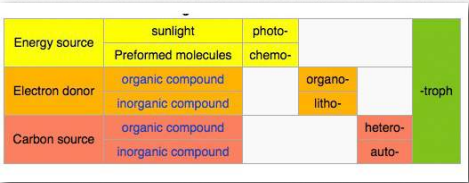
Figure 1.4 – Organization of organisms by metabolic type Wikipedia
All cells obtain and use energy. The source of this energy is different in different organisms (Figure 1.4). Phototrophs are organisms that obtain metabolic energy from light, while chemotrophs get their energy from the oxidation of chemical fuels. Organisms that can capture energy from light or from chemical sources are termed autotrophs (auto=self, troph=nourishing). Others organisms are heterotrophs, which use the organic compounds made by other organisms as their energy source. Plants and other photosynthetic organisms are autotrophs. Animals such as ourselves are heterotrophs.
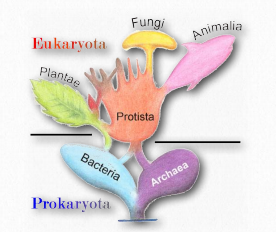
Figure 1.5 – Tree of life Wikipedia
Cells may be aerobic (i.e., use oxygen) or anaerobic (able to live without oxygen). Some anaerobic cells require an environment free of oxygen, and are referred to as obligate anaerobes. Others are cells that can live with, or without, oxygen, and are called facultative anaerobes.
Prokaryotic and eukaryotic cells
Organisms may be divided into two major groups, the prokaryotes and the eukaryotes. The cells of the former lack a nucleus and other organelles, while those of the latter are characterized by numerous internal, membrane-bounded compartments, including a nucleus.
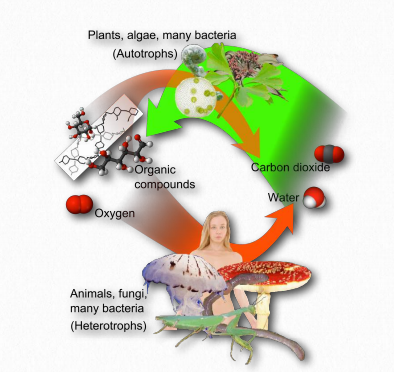
Figure 1.6 – Interplay between autotrophs and heterotrophs Wikipedia
Prokaryotes are unicellular and generally considerably smaller than their eukaryotic cousins, with sizes ranging from 0.5 to 5 µm in diameter. Prokaryotes typically have circular chromosomes, and may sometimes contain extra-chromosomal DNA elements (also Image by usually circular) called plasmids. Although the DNA in prokaryotes is not wrapped around histones, as is the case for eukaryotes, prokaryotes have proteins associated with their DNA. The DNA-protein complexes in prokaryotes create a structure called a nucleoid, which is different from the eukaryotic nucleus in not being enclosed by a nuclear envelope (Figure 1.7).

Aleia Kim Table 1.1
Prokaryotes may be divided into two broad categories, bacteria and archaea. These single-celled organisms are both ancient and widespread. Archaea were once thought to be a subgroup of bacteria, but have subsequently been shown to be a completely different group of organisms that are so distinct from both bacteria and eukaryotes that they now are classified in a domain of their own.
Bacteria
Like eukaryotic cells, bacterial cells have a plasma membrane surrounding them, but in addition, they also contain an exterior cell wall, comprised of an interlocked peptidoglycan network. On their exterior surfaces, bacteria have hair-like appendages called pili that allow them to adhere to other cells. Pili play an important role in bacterial conjugation, a process in which DNA is transferred between bacterial cells. In addition, bacterial cells may have flagella that enable them to move through their surroundings.
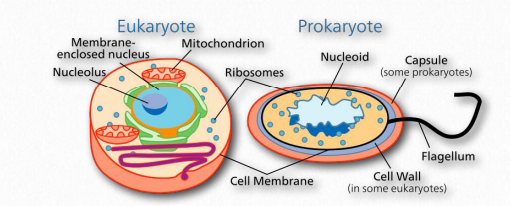
Figure 1.7 – Prokaryotic vs. eukaryotic cell structures (not to scale)
Interestingly, bacteria can communicate using chemical signals, in a process called quorum sensing. These signaling mechanisms enable bacteria to assess conditions around them. Quorum sensing plays a role in the process of infection by bacterial pathogens as well as the formation of biofilms.
Archaea
The first archaeans to be studied were all found in harsh environments such as salt flats and hot springs. They were initially believed to live only in such extreme environments (Figure 1.8). We now know that archaeans can be found in every environment, moderate or extreme. Archaea have been found in the human gut, and in such huge numbers in marine plankton that it has been suggested that they may be the most abundant organisms on earth.
While they are unicellular and superficially resemble bacteria, archaea are in some respects more similar to eukaryotes. Their molecular machinery and ribosomes are much more like those of eukaryotes than of prokaryotes. Archaea are unique among living organisms in their use of ether linkages to join the lipids used in their plasma membranes to glycerol. Not only are the ether linkages different from the ester linkages in all other forms of life, but the lipids themselves are different. In place of the fatty acids used in both bacterial and eukaryotic membranes, archaea use long isoprene-derived chains (Figure 1.9) This difference in membrane composition and structure makes archaeal membranes highly stable and may be advantageous in extreme conditions.

Figure 1.8 – Archaeans growing in acid mine waste
Like bacteria, archaea have a cell wall, but the composition is different. Some archaea have peptidoglycan-like molecules in their cell walls, while others build their cell walls entirely of glycoproteins and polysaccharides.
Eukaryotes
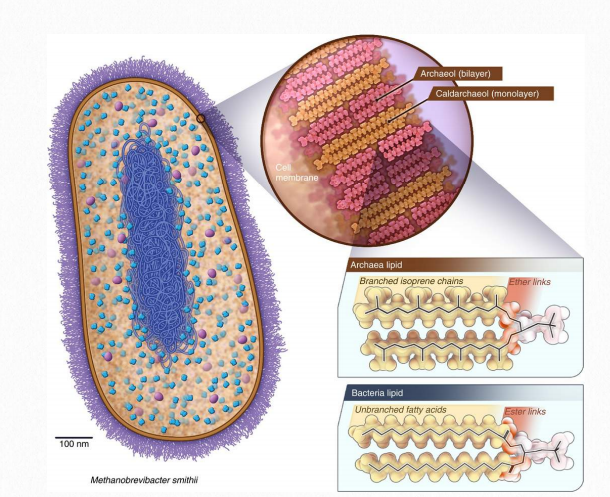
Figure 1.9 Archaeal membrane, top, showing unusual ether linkages and isoprene chains and bacterial membrane, below. Wikipedia
Eukaryotic cells are found in both unicellular and multicellular organizational schemes. Unicellular forms include yeast and many protists like Paramecium and Amoeba. Multicellular eukaryotes include plants, animals, and fungi. Eukaryotic cells are surrounded by a plasma membrane. Animal cells have no cell walls, whereas plant cells use cellulose, hemicellulose, and pectins to build cell walls outside their plasma membranes. Fungal cells have cell walls that contain the polymer chitin, which is also found in the exoskeletons of arthropods.
Figure 1.10 Paramecium Wikipedia
Eukaryotic cells are typically much larger (typically 10-100 µm) and contain considerably more DNA than prokaryotic cells. The most distinctive feature of eukaryotic cells, however, is the presence of a variety of internal membrane-bounded structures, called organelles.
Organelles
Eukaryotic cells are characterized by internal membrane-bounded compartments, or organelles. These compartments divide up the interior of the cell into discrete parts that have specialized functions.
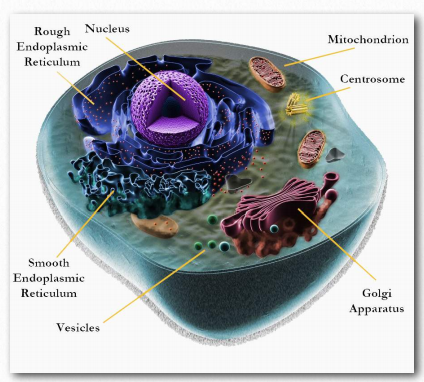
Figure 1.11 Animal cell structure Wikipedia
The presence of multiple compartments within the cell permits reactions requiring specific conditions to be carried out in isolation from the rest of the cell. For example, the formation of disulfide bonds in proteins is possible in the conditions within the endoplasmic reticulum, but would not readily occur in the different environment of the cytosol. The presence of membrane-bounded compartments also allows reactants to be more concentrated because of the smaller volume of the organelle.
Eukaryotic DNA in a cell is divided into linear bundles called chromosomes. Chromosomes contain the genomic DNA wrapped around cores of proteins called histones. The ends of linear eukaryotic chromosomes have telomeres, containing short repeated DNA sequences.
The chromosomes in eukaryotic cells are surrounded by the nuclear envelope, a double membrane structure that encloses the nucleus (Figure 1.12). Within the nucleus, there are enzymes required for the replication and transcription of genetic information. The presence of the nuclear envelope also regulates which proteins can enter the nucleus at any given time.
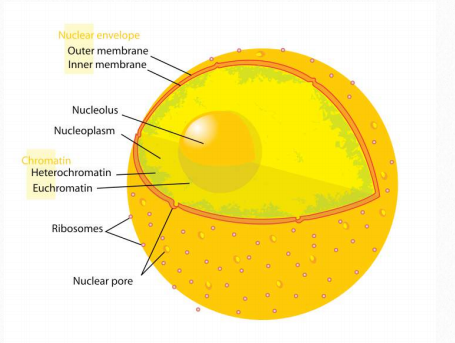
Figure 1.12 Cell nucleus
Mitochondria and chloroplasts have their own DNA, separate from and in addition to the nuclear DNA. This DNA is small and circular and resembles a prokaryotic chromosome. Mitochondria and chloroplasts also have their own ribosomes and tRNAs and can carry out their own protein synthesis. These organelles are likely derived from prokaryotes that once lived as endosymbionts within ancient eukaryotic cells and eventually became integrated into their host cells.
The cytoskeleton
Another interesting feature of eukaryotic cells is the presence of an internal skeleton-like structure called a cytoskeleton. The cytoskeleton is made up of a network of interlinking protein fibers Figure 1.13).
Although the word “skeleton” may suggest a rigid and fixed structure, the cytoskeleton is dynamic, with both microfilaments and microtubules disassembling and rearranging themselves on an ongoing basis, as needed.
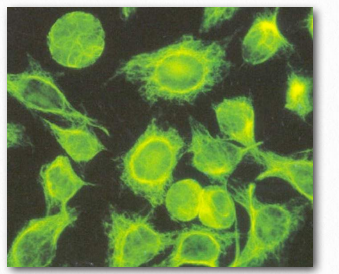
Figure 1.13 Cultured cells stained to show intermediate filaments Wikipedia
Figure 1.14 – β-tubulin in Tetrahymena Wikipedia
The cytoskeleton helps to organize the contents of the cell. Interactions among cytoskeletal proteins and components of the extracellular matrix are crucial in maintaining tissue structure.
Tissues
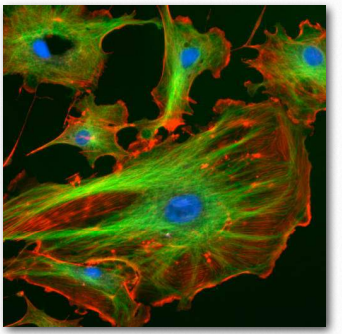
Figure 1.15 – The cytoskeleton. Actin filaments are in red, microtubules in green, nucleus in blue
Cells in multicellular organisms are organized into tissues that play specialized roles in the body. Animals have four types of tissues in their bodies – epithelium, connective tissue, nerve tissue, and muscle tissue.
Connective tissue
Of the four animal tissues, connective tissue is the one that serves as the “glue” to hold everything together. Connective tissue fills the gaps between all the other tissues of the body, including the nervous system.
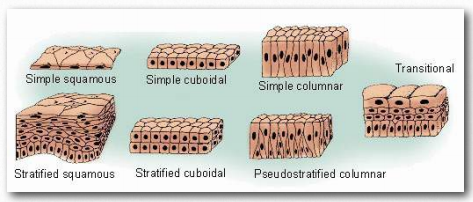
Figure 1.16 – Types of epithelial tissue
Nerve tissue
The nervous system of humans contains two main components. The brain and spinal cord comprise the central nervous system (CNS) and nerves branching from these make up the peripheral nervous system.
Nerve cells are also called neurons. Neurons can transmit and receive signals.
Nervous system functions include receiving input from senses, controlling muscles and glands, homeostasis, integration of information, and mental activity.
Muscle tissue
Mammals have three types of muscle tissue – 1) skeletal/striated muscle; 2) smooth, non-striated muscle; and 3) cardiac muscle. Cardiac muscle and smooth muscle are notable for contracting involuntarily. Both can be activated through nerve stimuli from the central nervous system or by innervation from the peripheral plexus or by endocrine/hormonal activation. Striated muscles, by contrast, only contract voluntarily by (mostly) conscious action influenced by the central nervous system.
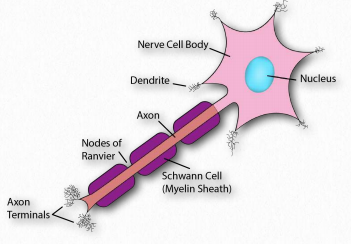
Figure 1.17 – Nerve cell anatomy Image by Pehr Jacobson

