Suppose–and we decided to be a bit cheeky here–that an economy only produces two things: ‘Likes’ and ‘Retweets’. These are like corn and steel, but…let’s say…modernized. We can think about this as an economy with two sectors: the Likes Sector, which uses both Likes and Retweets to produce Likes; and the Retweets Sector, which also uses both Likes and Retweets, but to produce Retweets.

Now, let’s say that the economy doesn’t produce any extra Retweets over time, but it does produce a surplus of Likes. That is, in a given period of production, the system will use up as many Retweets as it produced in the previous period, but it will produce more Likes than it uses. To be more specific, let’s say the model looks like this:

Likes Sector: [latex]10L + 60R → 310L[/latex]

Retweets Sector: [latex]48L + 2R → 62R[/latex]

In the above depiction, the left-hand side of the arrows indicates Likes and Retweets used up in production, and the right-hand side shows the output produced. We could also illustrate this as:

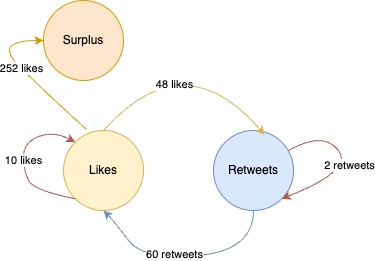
Note that a total of 62 Retweets are used in production and the total Retweet output is 62. Hence, there is no surplus of Retweets being generated. However, while the Likes Sector produces 310 Likes, the whole system only uses 10 + 48 = 58 Likes in production. This tells us that the system (the economy) is producing a surplus of 252 Likes.

Now we want to determine the relative prices of our two goods–that is, how much is a Retweet worth in terms of Likes, or vice versa? To figure this out, we’ll need to make an assumption: the surplus of Likes are distributed as profits with the rate of profit being the same between the two sectors. So let’s break down what profits and profit rates look like for each sector.

Profit and Profit Rates

We’ll conceptualize profit rates as net returns (profits) in the sector divided by total outlays by the sector. The Likes sector’s profits are the total Likes produced, less the Likes used up in production, and less the Retweets they had to purchase from the other sector for production. That comes to 310 Likes produced minus 10 Likes used up in production minus 60 Retweets also used up in production. Now, to get the profit rate we divide by the sector’s outlays–that is, what was used in production: 10 Likes and 60 Retweets. Hence, the rate of profit for the Likes sector can be written as:

[latex]\text{Rate of Profit}_\text{Likes} = \frac{310L - 10L - 60R}{10L + 60R}[/latex]

The profit rate for the Retweet sector is a bit simpler because it doesn’t produce a surplus. The Retweet sector’s profits are simply the value of the Retweets sold to the Likes sector less the cost of the Likes purchased from the Likes sector. As you can see in the model above, the Likes sector used 60 Retweets, which are the sales (or revenues) of the Retweets sector. Likewise, the Retweets sector used 48 Likes, which are its purchases from the Likes sector (or costs). Hence, the net returns to the Retweets sector comes out to 60 Retweets minus 48 Likes. And, just like we did before, to get the sector’s profit rate, we divide that by the sector’s outlays:

[latex]\text{Rate of Profit}_\text{Retweets} = \frac{60R - 48L}{48L + 2R}[/latex]

Solving for Relative Prices

Now that we know the two sectors’ profit rates, we can return to the assumption made above and set up the equation that will ultimately tell us relative prices. Since profit rates are equal between the sectors the equation simply sets the two profit rates above equal:

[latex]\text{Rate of Profit}_\text{Retweets} = \text{Rate of Profit}_\text{Likes}[/latex]

[latex]\frac{60R - 48L}{48L + 2R} = \frac{310L - 10L - 60R}{10L + 60R}[/latex]

Now for a bit of basic algebra. First, cross-multiply so we don’t have to deal with fractions:

[latex](60R - 48L)(10L + 60R) = (310L - 10L - 60R)(48L + 2R)[/latex]

A bit more algebra will get us to the result we’re looking for, but before that, we’re going to do a little trick. Since we’re only interested in the relative prices between the two products, we can treat one of them as a numeraire, which, to make a long story short, means we can drop one of the letters in our equation and just solve for the other. We’ll make Likes the numeraire and solve for R, which will give us the value of Retweets in terms of Likes. Thus, the equation becomes:

[latex](60R - 48)(10 + 60R) = (310 - 10 - 60R)(48 + 2R)[/latex]

Notice, all we did in the above equation is drop the L’s from the previous equation. Now multiply through to get:

[latex]600R+3,600R^2-480-2,880R = 14,880+620R-480-20R-2,880R-120R^2[/latex]

We can reduce each side down to:

[latex]3,600R^2 - 2,280R - 480 = -120R^2 -2,880R + 14,400[/latex]

The term -2,280R shows up on both sides, so that will cancel out. Then we can move the -120R² on the right to the left by adding 120R² to both sides. And we can move the -480 on the left to the right by adding 480 to both sides. This gives us:

[latex]3,720R^2 = 14,880[/latex]

Divide both sides by 3,720 to get:

[latex]R^2 = 4[/latex]

And finally, take the square root of both sides to get:

[latex]R = 2[/latex]

(Technically, it would be plus or minus 2, but since a negative price doesn’t make sense for our model, we’ll just keep the positive value.)

This means that one Retweet is worth 2. Two what? Two Likes. So, whatever dollar value you might want to give a Like, according to our model a Retweet would have to sell for twice as much for the economy to (1) sustainably distribute Likes and Retweets between the two sectors to ensure continued production of 62 Retweets and 310 Likes each period; and (2) as we assumed earlier, distribute the surplus in the form of profits between the two sectors so that the rate of profit is equal.