Let’s review the basic properties of the orthodox theory of the firm as given in previous chapters (“Cost Assumptions for Profit Maximizing Firms,” “Perfect Competition,” and “Monopoly”).  To keep things simple, we’ll focus on the short run behavior of a single firm, and we’ll look to the similarities of this behavior regardless of whether the market is competitive or monopolistic.  First, the firm is portrayed as a functional relationship between inputs (factors) and outputs (products).  Because we’re considering the short run, there are variable and fixed inputs, and therefore variable and fixed costs.

Second, the firm accepts the demand for its product as given and determines how much it should produce—its quantity of output (Q)—so that its profits are maximized.  The output that maximizes profits is where the cost of producing the last unit equals the revenue from selling it—that is, where marginal cost (MC) equals marginal revenue (MR).  Orthodox economists assume that the firm is subject to diminishing marginal returns, and therefore marginal cost will always eventually rise to meet marginal revenue and will cause average total cost (ATC) to eventually rise (giving it its ‘U’ shape).  Hence, the very simple Hypothesis 1: over some short-run period, managers are aware of their firms’ marginal cost associated with increasing (or decreasing) output, and they generally find that marginal cost increases over a relevant range of production.

Now, consider the conditions presented in the chapters “Cost Assumptions for Profit Maximizing Firms” and “Perfect Competition”:

1. If MC < ATC, then ATC is decreasing (marginal cost is ‘dragging down’ average total cost the same way a low test score would drag down your course grade).  Therefore, if ATC is decreasing, it must be the case that MC < ATC.
2. Profits = Q(P-ATC), where P represents price.  Therefore, firms make losses when P < ATC, break even when P = ATC, and make profits when P > ATC.
3. Profit maximizing firms under perfect competition produce where MC = MR = P.

We can read these three conditions in reverse to establish a necessary condition for firms to avoid making a loss.  Plugging (3) into (2), it should be clear that, since the firm will produce where P = MC, the profit equation can be restated as Profits = Q(MC – ATC) under perfect competition.  Hence, if the firm is going to break even or make a profit then MC must be ≥  ATC.  Taking this back to (1), then, for MC to be equal to or greater than ATC, ATC must either be constant or increasing at some reasonable level of output.

Hence, Hypothesis 2: if firms maximize profits by producing a quantity where marginal cost equals marginal revenue, then under competitive conditions firms must normally be producing in a situation in which average total cost is either constant or increasing.  Really, this is just an extension of hypothesis one which allows us to test our theory by looking at average total costs rather than marginal costs.

Testing the Theory

It is generally held that a developed science should be capable of expressing ideas about how the world works in hypotheses, and that these hypotheses should be compared with actual observations to determine how well the theory explains what we see in the real world.  Fortunately (and perhaps surprisingly), a considerable number of studies on both costs and prices have been produced going back over 100 years.  Saving the reader a laborious trek through all of them, we’ll just look at a couple to test the validity of our hypotheses.

In 1998 Alan Blinder and colleagues published a book, Asking About Prices, which was not actually concerned with microeconomics (it was concerned with testing theories of macroeconomic price ‘stickiness’), but just the same can help us test our hypotheses [1].  Their approach was somewhat uncommon to orthodox economics at the end of the 20th century: they simply asked business people about how they did things.  For our purposes, their work on marginal costs (see p. 103) sheds light on hypothesis 1.  Asking business executives about the shape of their marginal cost curve was apparently a bit tricky.  Evidently, most do not normally consider the concept of marginal cost, so the surveyors had to repeat, rephrase, and further explain the question before a response could be given.

And the responses were not encouraging for the orthodox theory of the firm.  Firms representing only 11% of GDP were believed to have upward sloping marginal cost curves.  Nearly half reported constant marginal costs, and, almost shockingly, 41% reported decreasing marginal costs (suggesting increasing returns).  Evidently, the ‘law’ of diminishing marginal returns is more like a local custom, appropriate to only a small part (about 11%) of the US economy.

In fact, similar findings had been reported over 50 years ago.  In an article published in the American Economic Review in 1952, Wilford Eitemen and Glenn Guthrie reported their findings from a survey of manufacturing companies across the US.  Specifically, they found that only 5% of the goods produced conformed to the standard ‘U’-shaped depiction of average total costs.  The majority (60%) of products were reported as having average total cost curves which simply declined as output increased up to full capacity.  (Almost all remaining products were reported as similar but with a slight rise in average total costs just before capacity was reached.)

Designing the Average Total Cost Curve

Eitemen offered a simple, intuitive reason why we should expect that most average total cost curves would always decline with increased output.  One way to look at the matter is in terms of the percentage of designed full capacity output at which you would want your production process to operate most efficiently.  To give an example, imagine you’re an engineer and you have been tasked with designing a machine (or a factory, or the layout of an office) that can produce some maximum number of units in a given day.  In designing the machine, you find that it will have to operate more or less efficiently depending on how heavily it’s being used.  Would you design it to operate most efficiently when it’s only running at 20% capacity?  Maybe 60%?  Perhaps 99%?

Most would say that a production process should work best when it’s operating somewhere near the level of output it was designed to be capable of producing–otherwise, why should it be made to produce so much output in the first place?  Translate ‘work best’ into ‘operate at lowest average total cost’ and the implication should be clear: a ‘U’-shaped average total cost curve indicates a production process that was designed to be capable of producing up to some maximum amount inefficiently.  In contrast, a declining average total cost curve indicates that the production process was made to work best when it’s producing as much as it was designed to be capable of producing–the most efficient, lowest average total cost point being at or near 100% of full capacity output.

Just to be sure that this argument makes sense for a large range of designed production processes, let’s consider a scenario in which it’s simply impossible to engineer a machine that’s capable of efficiently producing the desired level of output.  For example, you, the engineer, were tasked with designing a machine that could produce 1,000 units (of whatever) per hour, but you’ve determined that this is only possible if the machine is run in such a way as to generate extreme friction, frequent downtime for maintenance, and wasted materials.  You find that it’s possible to create a machine that doesn’t have these problems, but it would only be capable of producing 500 units per hour.  You report the situation back to your boss; what does she say?

The boss is likely to say ‘fine, let’s make two machines that produce 500 units per hour efficiently’.  After all, there’s little sense in setting up a production process that we know at the outset is going to waste material and break down all the time.  And with two of the efficiently producing machines, we can still hit our target of 1,000 units per hour just as well.

Whether one machine that can produce efficiently at 1,000 units per hour, or two at 500 units per hour, the implication for the cost curves associated with this production process is essentially the same. Those cost curves are illustrated in figure 1, below.

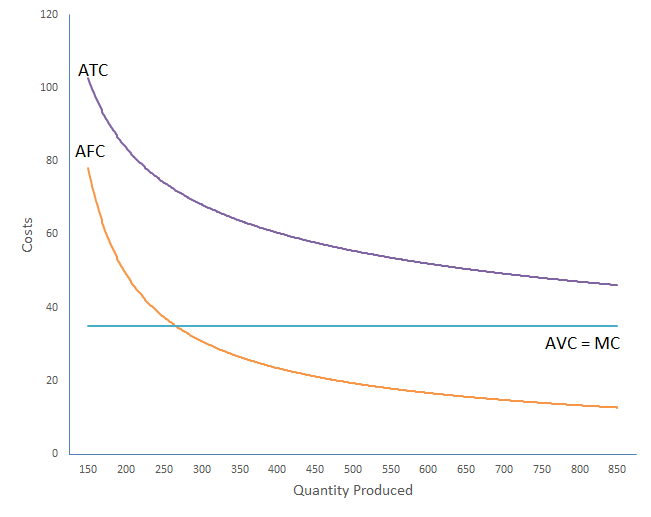
Notice that average total cost is relatively high when output is low, but declines as output increases. In the simplest sense, you could think of this in terms of machines that produce more efficiently when they’re run at or near the range at which they were designed to produce.  Thinking of it this way, average variable cost simply represents the material and labor costs per unit, which are most likely going to be the same regardless of how much is being produced in a given period of time, since, when the machine isn’t being used, the workers won’t be working and materials won’t be processed. This means that the additional cost per unit produced (marginal cost) is the same as average variable cost, and hence is also constant.

But really this cost structure is likely to represent not just a single machine (or pair of machines), but a more general production process. Whether it’s a machine shop, a grocery store, a restaurant, or an office, these production processes are typically designed to operate efficiently up to or near the point of full capacity—that is, the most they’re designed to be capable of producing. They will include fixed inputs which are used over longer periods of time, and variable inputs used more or less immediately in the production processes.  And because variable cost will generally be constant (although in some cases it may actually decline), average total cost will have the same shape as average fixed cost—declining as those costs are spread over larger quantities of output—but raised by the constant amount of average variable cost.

Is agriculture an exception?

Okay, you might be thinking, but this applies to manufacturing contexts–or really any production process that gets designed by people.  What about industries that deal directly with the constraints imposed by nature herself–for instance, farming? Doesn’t the ‘law’ of diminishing marginal returns still apply here?The answer: maybe, but maybe not.  Recall the example given in Chapter 23, Section 23.3, “The Structure of Costs in the Short Run.”  There, it was argued that irrigating farmland–that is, adding water as a variable input to a fixed input of soil–follows the same cost structure as orthodox economists assume to be the case for most firms: adding more water to the land initially produces larger and larger increases in crop output, but, crucially, diminishing returns set in eventually and the output you get from adding more water gets smaller and smaller.Suppose those numbers are accurate for a market garden with 10 acres of land.

The numbers in Table 1 below are the same as in chapter 23, with the first column giving the amount of average daily water used per acre per day, and output given in hundreds of pounds of produce per year.  Notice that marginal cost decreases as more water is added initially, but beginning with the third unit of water marginal cost increases due to diminishing returns.

Table 1. Water, Output, and Costs

Water	Output	Fixed Cost	Variable Cost	Total Cost	Marginal Cost
1	16	$160	$80	$240	$5.00
2	40	$160	$160	$320	$3.33
3	60	$160	$240	$400	$4.00
4	72	$160	$320	$480	$6.67
5	80	$160	$400	$560	$10.00

However, it must be emphasized here that diminishing returns to watering only becomes an issue because in this short-run situation, there is by definition a fixed amount of land and because we assume that the land is fully employed. Of course, if the available land weren’t fixed then we wouldn’t be in the short run, but what about the second part? What if the farmer were able to produce the output he desired without using all the land he had?

In this case, it would be more efficient, less costly, and therefore more profitable to water only a fraction of the total land up to the point just before diminishing returns kicked in.  With the numbers in Table 1 above that would be 2 units of water.  So, if our table represents costs for 10 acres of land then producing 80 units of output will require 5 units of water at a (variable) cost of $400. But what if the farmer only desired to produce 16 units of output? You might think that this would require one gallon of water, giving the costs in the first row of Table 1, making for a variable cost of $80. But that’s not quite right. If the farmer instead used two gallons of water per acre, but only grew on 4 acres, then he would get 40% of the output indicated in the second row of Table 1, which comes out to 16. And, since he only watered 4 acres instead of 10, his variable cost should only be 40% of what is indicated in the table–that is, 0.4 × $160 = $64.

This was a point made by economist Pierro Sraffa way back in 1925 (and explained in more detail by contemporary economist Steve Keen in his Debunking Economics). In essence, even where diminishing returns are present in the production processes–for instance, when they are imposed by nature–they can still be avoided so long as the output desired is smaller than what can be produced efficiently with only a fraction of the land or other fixed input. And wherever and whenever this is the case, the producer will use the same amount of variable input per unit of fixed input (in our example, water per acre of land), and simply vary the amount of fixed input used.

The main implication? Variable cost per unit of output (AVC) doesn’t change as output increases or decreases (up to the point of full employment of the fixed input), giving the same basic shape of our cost curves as in Figure 1 above.

Implications for the Orthodox Theory of the Firm

Returning to the three postulates we used to develop hypothesis 2, Eitemen and Guthrie’s findings indicate a clear departure from the standard model of firm behavior.  If most firms believe their average total costs decline as output increases, then mathematically their marginal cost curves must be below (‘dragging down’) their average total costs.  (This would be the case if the firm’s marginal costs are constant or declining with increased output, as Blinder et al. indicate is common throughout the economy.) Now, if marginal costs are always less than average total costs, then there are only two possible conclusions to be drawn:

1. Firms produce a quantity where MC = MR.  But, since MC is always < ATC, and under perfect competition profits = Q(MC-ATC), then firms in perfectly competitive markets will always make a loss.  This doesn’t seem like an attractive conclusion–surely we can find firms in competitive markets that manage to make a profit.  So it’s worth considering the alternative:
2. Firms do not produce a quantity where MC = MR.  That is, under the cost structure that most firms report, the standard profit maximization behavior postulated in the orthodox theory of the firm is not only unrealistic, it’s impossible.

Clearly, the implications of these findings do not bode well for the orthodox theory of the firm presented in earlier chapters.  The preponderance of evidence may not wholly refute the orthodox model, but it does expose severe limitations. In the breakout box below, two additional hypotheses are examined, giving greater reason to abandon the orthodox theory of the firm.  The section that follows then introduces a few basic concepts from an alternative, heterodox viewpoint.

Two More Hypotheses

From the orthodox perspective, we can imagine a firm incrementally increasing its, say, weekly output, and continuing to do so as long as its marginal revenue is greater than its marginal cost.  Once the additional revenue of one additional unit of output just covers the cost of that unit’s production, the firm settles on that level of output–profit maximizing equilibrium has been reached where MC = MR.  Assuming that marginal cost must be positive (most workers won’t pay their boss to let them work more hours, but perhaps there are exceptions), then marginal revenue must also be positive.Now, refer back to chapter “Elasticity,” specifically the section asking “Does Raising Price Bring in More Revenue.”  There you learned that a firm that is able to set its own price can increase revenues by cutting prices if demand is elastic.  If on the other hand demand is inelastic, cutting your price will increase your sales (that’s the law of demand after all), but the lower price will weigh heavier on your revenues than the gained sales, and your revenues will actually decline.  Mathematically, this works out to a simple rule: if demand is elastic then selling more will increase revenues–which is to say that marginal revenue is positive when the elasticity of demand > 1 (and MR is zero when the elasticity of demand = 1, and negative when elasticity of demand is < 1).  Hence, hypothesis 3: If firms produce where MC = MR, then MR must be positive, and therefore demand must be elastic.

Blinder et al. (1998 p. 99) found some support for this–but not much.  While noting many businesses do not actually calculate or even think along these lines, the authors found that, among those that could give an answer, 84% believed demand to be inelastic (and, by implication, negative marginal revenue).  In fact, 41% believed that the elasticity of demand was zero–that is, a price cut would not increase sales at all–which is literally as inelastic as it can get.

Now consider a more general issue.  In chapter “Supply and Demand” you were introduced to the centerpiece of orthodox economics: the market model. The chief argument of that model is that prices in the market will adjust to bring supply and demand into an equilibrium in which the quantity people wish to sell is equal to the quantity people wish to purchase–that is, the price mechanism acts to clear markets.  This model fits into the broader narrative of orthodox thought which holds that capitalist economies are organized by price adjustments in the complex network of markets that make up these economies. Therefore, Hypothesis 4: unless the world changes very seldom or very slowly, leaving most markets in their previously established equilibria for long stretches of time, prices should be changing rapidly with frequent bidding, as in an auction market.

By now you could probably predict what the evidence was going to tell us about this important part of standard orthodox theory: throughout most of the modern US economy prices change relatively infrequently.  Blinder et al. (1998, p. 84) find that 49% of responding firms change their prices no more than once in a year or even longer.  Indeed, only 22% reprice daily, weekly, or monthly.  The auction market model at the core of orthodox economics exists, indeed; but, it would appear that it lies somewhere between minor and insignificant in today’s economy.

References

Blinder, Alan, et al. Asking about prices: a new approach to understanding price stickiness. Russell Sage Foundation. 1998.

Keen, Steve. Debunking Economics: The Naked Emperor Dethroned? Zed Books. 2011

Sraffa, Priero. “The Laws of Returns under Competitive Conditions.” The Economic Journal, Vol. 36, No. 144, pp. 535-50. 1926.