1 Order of Operations
We’ll begin with a look at order of operations. In many situations in life, the order in which we perform certain actions is important. For example, if you are putting on your shoes and socks, you need to put a sock on your foot before you put a shoe on that foot. However, if you put on your left sock first, it doesn’t really matter whether the next thing you put on is your left shoe or your right sock, as long as you don’t try putting on your right shoe next. A multi-step math calculation can be the same way; you might have some steps that need to happen in a specific sequence, but there may be some steps that you can do in whatever order you prefer.
Evaluating an Expression
To evaluate an expression means to simplify it and find its value.
Exercises
- Evaluate by performing the addition first:
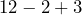
- Evaluate by performing the subtraction first:
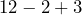
When we evaluate an expression, we want to have a single correct answer. It isn’t very helpful for the answer to be “maybe 7, or maybe 13”. Mathematicians have decided on an order of operations, which tells us which steps should be done before other steps. You can think of them as the rules of the road.
Order of Operations: PEMDAS
P: Work inside of parentheses or grouping symbols, following the order PEMDAS as necessary inside the grouping symbols.
E: Evaluate exponents.
MD: Perform multiplications and divisions from left to right.
AS: Perform additions and subtractions from left to right.
Exercises
Evaluate each expression.
Based on Exercises 3 & 4, we can see that Exercise 1 told us to use the wrong order of operations. If there are no parentheses, we must evaluate by first performing the subtraction and then performing the addition.
Before we move on, you should be aware that there are a handful of ways to show multiplication. All of the following represent 
:
In this textbook, you will most often see the dot, like , or parentheses directly next to a number, like . We tend to avoid using the symbol because it can be mistaken for the letter x.
Exercises
Evaluate each expression.
Exponents
An exponent indicates repeated multiplication. For example, 
and 
. The exponent tells us how many factors of the base are being multiplied together.
Exercises
Evaluate each expression.
Grouping Symbols
In the next set of exercises, the only differences are the parentheses, but every exercise has a different answer.
Exercises
Evaluate each expression.
It is possible to have grouping symbols nested within grouping symbols; for example, 
.
To make it somewhat easier to match up the pairs of left and right parentheses, we can use square brackets instead: ![7+(5^2-[3(17-12\div4)+2\cdot5]\div4)](https://openoregon.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-b87edf08166eeaba351077e46538009d_l3.png "Rendered by QuickLaTeX.com")
.
Exercises
Simplify the expression.
A fraction bar is another grouping symbol; it tells us to perform all of the steps on the top and separately perform all of the steps down below. The final step is to divide the top number by the bottom number.
Exercises
Evaluate each expression.
We will look at formulas in a later module, but let’s finish by translating from words to a mathematical expression.
Exercises
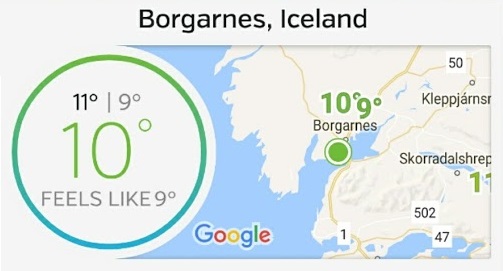
- You can find the approximate Fahrenheit temperature by doubling the Celsius temperature and adding
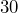. If the temperature is 
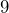°C, what is the approximate Fahrenheit temperature? Write an expression and evaluate it. - You can find the approximate Celsius temperature by subtracting 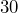from the Fahrenheit temperature and then dividing by
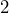. If the temperature is 
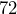°F, what is the approximate Celsius temperature? Write an expression and evaluate it.
to find the value
