Scientific Notation

Morgan Chase

11 Scientific Notation

“Number 10” by yoppy is licensed under CC BY 2.0

Powers of Ten

Decimal notation is based on powers of 10: 0.1 is $\frac{1}{10^1}$ , 0.01 is $\frac{1}{10^2}$ , 0.001 is $\frac{1}{10^3}$ , and so on.

We represent these powers with negative exponents: $\frac{1}{10^1}=10^{-1}$ , $\frac{1}{10^2}=10^{-2}$ , $\frac{1}{10^3}=10^{-3}$ , etc.

Negative exponents: $\frac{1}{10^n}=10^{-n}$

Note: This is true for any base, not just 10, but we will focus only on 10 in this course.

With our base 10 number system, any power of 10 can be written as a 1 in a certain decimal place.

$10^{4}$	$10^{3}$	$10^{2}$	$10^{1}$	$10^{0}$	$10^{-1}$	$10^{-2}$	$10^{-3}$	$10^{-4}$
$10,000$	$1,000$	$100$	$10$	$1$	$0.1$	$0.01$	$0.001$	$0.0001$

If you haven’t watched the video “Powers of Ten” from 1977 on YouTube, take ten minutes right now and check it out. Your mind will never be the same again.

Scientific Notation

Let’s consider how we could rewrite some different numbers using these powers of 10.

Let’s take 50,000 as an example. 50,000 is equal to $5\times10,000$ or $5\times10^4$ .

Looking in the other direction, a decimal such as 0.0007 is equal to $7\times0.0001$ or $7\times10^{-4}$ .

The idea behind scientific notation is that we can represent very large or very small numbers in a more compact format: a number between $1$ and $10$ , multiplied by a power of $10$ .

A number is written in scientific notation if it is written in the form $a\times10^n$ , where $n$ is an integer and $a$ is any real number such that $1\leq{a}<10$ .

Note: An integer is a number with no fraction or decimal part: … -3, -2, -1, 0, 1, 2, 3 …

Although we generally try to avoid using the “x” shaped multiplication symbol, it is frequently used with scientific notation.

Exercises

Earth and Mars are two of the smaller planets. Earth has a mass of approximately 5,970,000,000,000,000,000,000,000 kilograms, and Mars has a mass of approximately 639,000,000,000,000,000,000,000 kilograms. Can you determine which mass is larger?

Clearly, it is difficult to keep track of all those zeros. Let’s rewrite those huge numbers using scientific notation.

Exercises

Earth has a mass of approximately 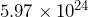$5.97\times10^{24}$ kilograms, and Mars has a mass of approximately 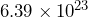$6.39\times10^{23}$ kilograms. Can you determine which mass is larger?

It is much easier to compare the powers of 10 and determine that the mass of the Earth is larger because it has a larger power of 10. You may be familiar with the term order of magnitude; this simply refers to the difference in the powers of $10$ of the two numbers. Earth’s mass is one order of magnitude larger because 24 is 1 more than 23.

Exercises

Suppose someone tells you their salary is “six figures”.

To the nearest dollar, what is their minimum possible salary? Write the answer in standard notation and in scientific notation.
To the nearest dollar, what is their maximum possible salary? Write the answer in standard notation and in scientific notation.

We can apply scientific notation to small decimals as well.

Exercises

The radius of a hydrogen atom is approximately 0.000000000053 meters. The radius of a chlorine atom is approximately 0.00000000018 meters. Can you determine which radius is larger?

Again, keeping track of all those zeros is a chore. Let’s rewrite those decimal numbers using scientific notation.

Exercises

The radius of a hydrogen atom is approximately 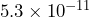$5.3\times10^{-11}$ meters. The radius of a chlorine atom is approximately 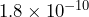$1.8\times10^{-10}$ meters. Can you determine which radius is larger?

The radius of the chlorine atom is larger because it has a larger power of 10; the digits 1 and 8 for chlorine begin in the tenth decimal place, but the digits 5 and 3 for hydrogen begin in the eleventh decimal place.

Scientific notation is very helpful for really large numbers, like the mass of a planet, or really small numbers, like the radius of an atom. It allows us to do calculations or compare numbers without going cross-eyed counting all those zeros.

Exercises

Write each of the following numbers in scientific notation.

$1,234$
$10,200,000$
$0.000870$
$0.0732$

Convert the following numbers from scientific notation to standard decimal notation.

$3.5\times10^4$
$9.012\times10^7$
$8.25\times10^{-3}$
$1.4\times10^{-5}$

Multiplying & Dividing with Scientific Notation

You may be familiar with a shortcut for multiplying numbers with zeros on the end; for example, to multiply $300\times4,000$ , we can multiply the significant digits $3\times4=12$ and count up the total number of zeros, which is five, and write five zeros on the back end of the $12$ : $1,200,000$ . This shortcut can be applied to numbers in scientific notation.

To multiply powers of $10$ , add the exponents: $10^m\cdot10^n=10^{m+n}$

Exercises

Multiply each of the following and write the answer in scientific notation.

$(2\times10^3)(4\times10^4)$
$(5\times10^4)(7\times10^8)$
$(3\times10^{-2})(2\times10^{-3})$
$(8\times10^{-5})(6\times10^9)$

When the numbers get messy, it’s probably a good idea to use a calculator. If you are dividing numbers in scientific notation with a calculator, you may need to use parentheses carefully. The following rule is true, but you may just want to use a calculator instead.

To divide powers of $10$ , subtract the exponents: $10^m\div10^n=10^{m-n}$

Exercises

New Jersey has the highest population density of the 50 states.^[1] Its population is 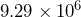$9.29\times10^{6}$ people and its land area is 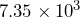$7.35\times10^{3}$ square miles. Divide these numbers to find the population density in people per square mile.
California has the highest population density of all states west of the Mississippi River.^[2] Its population is 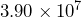$3.90\times10^{7}$ people and its land area is 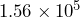$1.56\times10^{5}$ square miles. Divide these numbers to find the population density in people per square mile.
The mass of a proton is 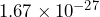$1.67\times10^{-27}$ kg. The mass of an electron is 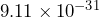$9.11\times10^{-31}$ kg. Divide these numbers to determine approximately how many times greater the mass of a proton is than the mass of an electron.

Engineering Notation

Closely related to scientific notation is engineering notation, which uses powers of $1,000$ . This is the way large numbers are often reported in the news; if roughly $37,000$ people live in Oregon City, we say “thirty-seven thousand” and we might see it written as “37 thousand”; it would be unusual to think of it as $3.7\times10,000$ and report the number as “three point seven ten thousands”.

One thousand = $10^3$ , one million = $10^6$ , one billion = $10^9$ , one trillion = $10^{12}$ , and so on.

In engineering notation, the power of $10$ is always a multiple of $3$ , and the other part of the number must be between $1$ and $1,000$ .

A number is written in engineering notation if it is written in the form $a\times10^n$ , where $n$ is a multiple of $3$ and $a$ is any real number such that $1\leq{a}<1,000$ .

Note: Prefixes for large numbers such as kilo, mega, giga, and tera are essentially engineering notation, as are prefixes for small numbers such as micro, nano, and pico. We’ll see these in Module 16.

Exercises

Write each number in engineering notation, then in scientific notation.

The U.S. population is around 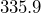$335.9$ million people.^[3]
The world population is around 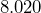$8.020$ billion people.^[4]
The U.S. national debt is around 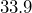$33.9$ trillion dollars.^[5]

Divide the U.S. national debt by the U.S. population to determine the amount of debt per person.

For a visualization of the relative sizes of a million, a billion, and a trillion, see this graphic made by Chris Kane, graphic artist and my friend from high school (PDF file).

Exercise Answers

Source: https://en.wikipedia.org/wiki/New_Jersey ↵
Source: https://en.wikipedia.org/wiki/List_of_states_and_territories_of_the_United_States_by_population_density ↵
Retrieved from https://www.census.gov/popclock/, January 1, 2024 ↵
Retrieved from https://www.census.gov/popclock/, January 1, 2024 ↵
Retrieved from https://fiscaldata.treasury.gov/datasets/debt-to-the-penny/, January 1, 2024 ↵

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License