Area of Regular Polygons

Morgan Chase

23 Area of Regular Polygons

You may use a calculator throughout this module.

an aerial view of the Pentagon building — “The Pentagon” by David B. Gleason is licensed under CC BY-SA 2.0

The Pentagon building spans $28.7$ acres ( $116,000\text{ m}^2$ ), and includes an additional $5.1$ acres ( $21,000\text{ m}^2$ ) as a central courtyard.^[1] (That’s roughly 25 American football fields… or 23 Canadian football fields.) In this module, we will focus on calculating the area of regular polygons such as this one.

A regular polygon has all sides of equal length and all angles of equal measure. Because of this symmetry, a circle can be inscribed—drawn inside the polygon touching each side at one point—or circumscribed—drawn outside the polygon intersecting each vertex. We’ll focus on the inscribed circle first.

Using the Distance from the Center to an Edge

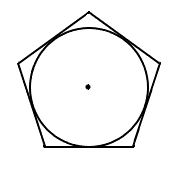
a circle inside a regular pentagon. the circle touches the center of all five sides of the pentagon. — inscribed circle

Let’s call the radius of the inscribed circle lowercase $r$ ; this is the distance from the center of the polygon perpendicular to one of the sides. (The inner radius is more commonly called the apothem and labeled $a$ , but we are trying to keep the jargon to a minimum in this textbook.)

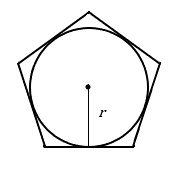
a regular pentagon with a circle inside it touching the center point of each side of the pentagon, and a radius drawn from the center straight down to the center of the bottom side, labeled lowercase r

We can derive a formula for the area of a regular polygon by dividing the polygon into equally-sized triangles and combining the areas of those triangles. If the length of each side of is $s$ , each triangle’s area is its base times its height divided by 2, or $s\cdot{r}\div2$ . If the polygon has $n$ sides, then there are $n$ of these triangles, and the total combined area is $n\cdot{s}\cdot{r}\div2$ .

Area of a Regular Polygon (with a radius drawn to the center of one side)

For a regular polygon with $n$ sides of length $s$ , and inscribed (inner) radius $r$ ,

$A=nsr\div2$

Note: This formula is more commonly written as one-half the apothem times the perimeter: $A=\frac{1}{2}ap$ . The apothem is what we’re calling $r$ , and the perimeter is $n\cdot{s}$ , so $A=\frac{1}{2}ap$ and $A=nsr\div2$ are equivalent formulas.

Exercises

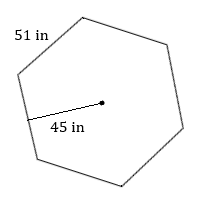
Calculate the area of this regular hexagon.
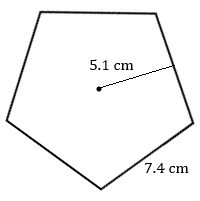
Calculate the area of this regular pentagon.
A stop sign has a height of 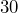$30$ inches, and each edge measures 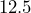$12.5$ inches. Find the area of the sign.

Using the Distance from the Center to a Vertex

Okay, but what if we know the distance from the center to a vertex (a corner of the polygon) instead of the distance from the center to an edge? We’ll need to imagine a circumscribed circle.

a circle outside a regular pentagon. all five corner points of the pentagon touch the circle. — circumscribed circle

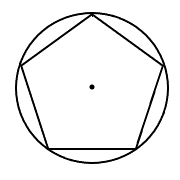
Let’s call the radius of the circumscribed circle capital $R$ ; this is the distance from the center of the polygon to one of the vertices (corners).

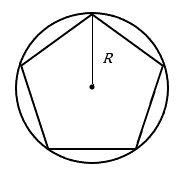
a regular pentagon inside a circle with all five corner points on the circle, and a radius from the center to one corner point labeled capital R

Area of a Regular Polygon (with a radius drawn to a vertex)

For a regular polygon with $n$ sides of length $s$ , and circumscribed (outer) radius $R$ ,

$A=0.25ns\sqrt{4R^2-s^2}$

or

$A=ns\sqrt{4R^2-s^2}\div4$

Your author created this formula because every other version of it uses trigonometry, which we haven’t covered yet. ^[2]

Exercises

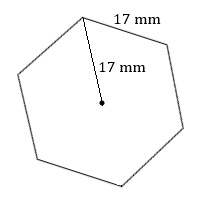
Calculate the area of this regular hexagon.
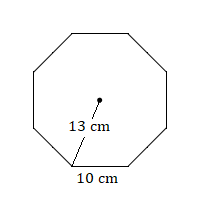
Calculate the area of this regular octagon.
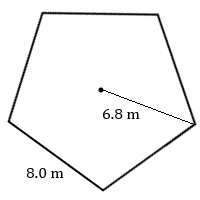
Calculate the area of this regular pentagon.

Fun fact: In a regular hexagon, the radius to a vertex is always equal to the side length. If you divide the hexagon into six equilateral triangles, you’ll see why.

Composite Figures with Regular Polygons

As you know, a composite figure is a geometric figure which is formed by joining two or more basic geometric figures. Let’s look at a composite figure formed by a circle and a regular polygon.

Exercises

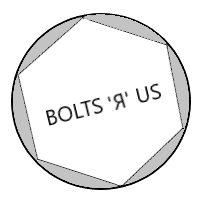
a hexagon labeled "bolts r us" inscribed in a circle

The hexagonal head of a bolt fits snugly into a circular cap with a circular hole with inside diameter 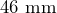$46\text{ mm}$ as shown in this diagram. Opposite sides of the bolt head are 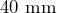$40\text{ mm}$ apart. Find the total empty area in the hole around the edges of the bolt head.

Exercise Answers

Source: https://en.wikipedia.org/wiki/The_Pentagon ↵
This formula is derived from dividing the polygon into n equally-sized triangles and combining the areas of those triangles; it includes a square root because it involves the Pythagorean theorem. ↵

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License