9 Percents Part 1
In this module, we will look at the basics of percents, and how percents are related to fractions and decimals. Then we will solve some straightforward percent problems.
We’ll return to percents in modules 12 and 27 and solve more complicated problems. This will give you a chance to develop your skills gradually without getting confused.
Percent Basics
The word percent means “per one hundred”. You can think of a percent as a fraction with a denominator of 100.
Exercises
- What percent of the squares are shaded blue?
- What percent of the squares are not shaded blue?
To write a percent as a fraction: drop the percent sign, write the number over 100, and simplify if possible. (Notice that if a percent is greater than 100%, the fraction will be greater than 1, and if a percent is less than 1%, the fraction will be less than 
.)
of Earth’s surface is covered by water.
of Earth’s land surface is permanent cropland.
of Earth’s atmosphere is carbon dioxide.
of the number of jobs in 2022.To write a percent as a decimal: drop the percent sign and move the decimal point two places to the left. (Notice that if the percent is not a whole number, the decimal will extend beyond the hundredths place.)
Exercises
Write each percent from Exercises 3 through 6 as a decimal.
To write a decimal as a percent: move the decimal point two places to the right and insert a percent sign.
Exercises
Write each decimal number as a percent.
To write a fraction as a percent, write the fraction as a decimal by dividing the numerator by the denominator, then move the decimal point two places to the right and insert a percent sign.
Alternate method: If the denominator of the fraction is a factor of 100, it can easily be built up to have a denominator of 
.
Exercises
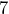out of 
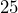students were tardy on Wednesday. Write 
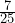as a percent.- A package of
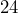m&m’s contained 
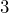orange m&m’s. Write 
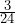as a percent.
Solving Percent Problems: Finding the Amount
You may use a calculator for the remainder of this module if needed.
We often use the words amount and base in a percent problem. The amount is the answer we get after finding the percent of the original number. The base is the original number, the number we find the percent of. (You may also think of the amount as the part, and the base as the whole.) We can call the percent the rate.
Be sure to change the percent to a decimal before multiplying.
Exercises
- What is
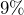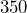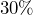of 
? 
of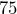 
is what number?- Find
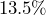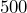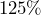of 
. 
of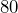 
is equal to what amount?- What number is
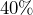of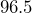 
? - Calculate
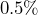of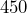 
.
Suppose you buy an electric drill with a retail price of 
in a city with 
sales tax.
- Find the amount of the tax. Round to the nearest cent, if necessary.
- How much do you pay in total?
- Source: https://en.wikipedia.org/wiki/Earth#Surface ↵
- Source: https://en.wikipedia.org/wiki/Earth#Surface ↵
- Source: https://en.wikipedia.org/wiki/Atmosphere_of_Earth#Composition ↵
- Source: Bureau of Labor Statistics, U.S. Department of Labor, Occupational Outlook Handbook, Heating, Air Conditioning, and Refrigeration Mechanics and Installers, at https://www.bls.gov/ooh/installation-maintenance-and-repair/heating-air-conditioning-and-refrigeration-mechanics-and-installers.htm ↵
