33 Non-Right Triangle Trigonometry

Your author among the California Redwoods.

You may use a calculator throughout this module.

Basic trigonometry applies to right triangles, but there are two useful formulas that can be used with non-right triangles; these are known as the Law of Sines and the Law of Cosines.

The Law of Sines allows you to use a proportion to solve for a missing value in a triangle.

The Law of Cosines is essentially the Pythagorean Theorem with an extra twist that makes it work with any kind of triangle.

These formulas have applications in many fields, most obviously in surveying and forestry where distances cannot be measured directly.

Law of Sines

Suppose we have a triangle with its vertices labeled A, B, C, and the sides opposite each vertex labeled a, b, and c.

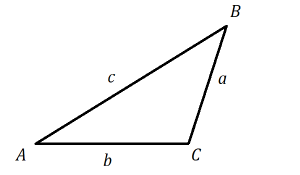
right triangle with acute angle A opposite side a, acute angle B opposite side b, and obtuse angle C opposite side c   right triangle with acute angle A opposite side a, acute angle B opposite side b, and acute angle C opposite side c

The Law of Sines is useful when you are dealing with two sides and two angles; if you know three of those values, you can use the formula to figure out the fourth value. Depending on which sides and angles you know, you’ll use one of these three versions:

\frac{\text{sin }A}{a}=\frac{\text{sin }B}{b}          \frac{\text{sin }B}{b}=\frac{\text{sin }C}{c}          \frac{\text{sin }C}{c}=\frac{\text{sin }A}{a}

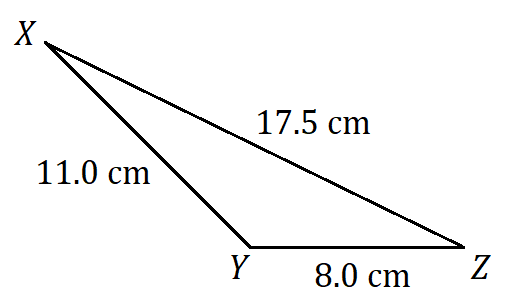
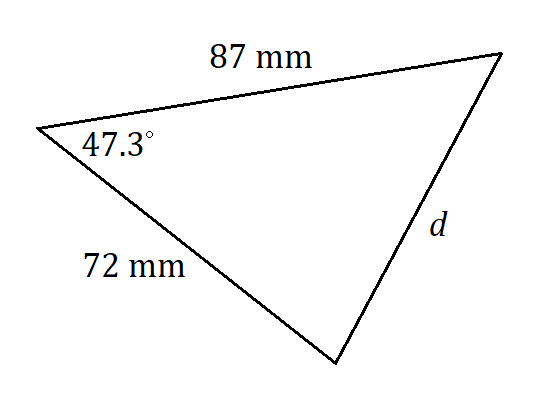
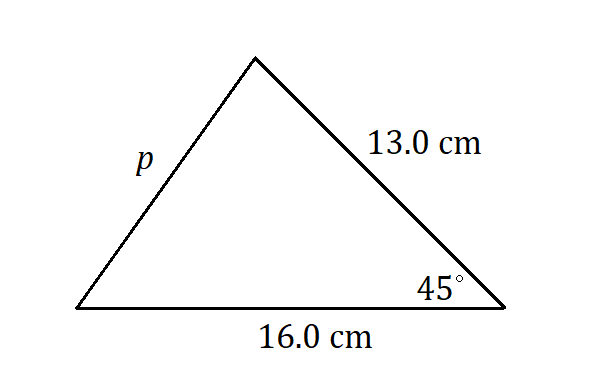
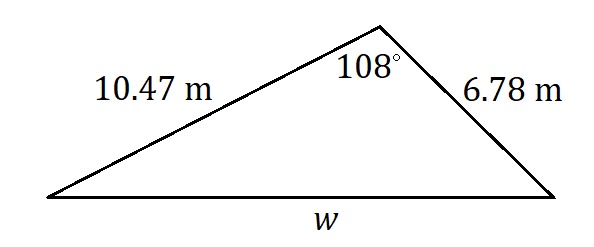
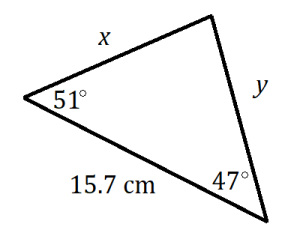
Exercises

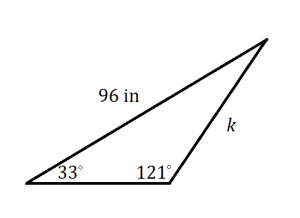
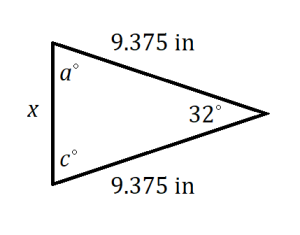
Determine the unknown value(s) in each triangle.

  1. obtuse triangle labeled from the top going counterclockwise: side 96 in, angle 33 degrees, unmarked side, angle 121 degrees, side k, unmarked angle.
  2. acute triangle labeled from the top going clockwise: side 9.375 in, angle 32 degrees, side 9.375 in, angle c degrees, side x, angle a degrees.
  3. acute triangle labeled from the top going counterclockwise: side x, angle 51 degrees, side 15.7 cm, angle 47 degrees, side y, unmarked angle.
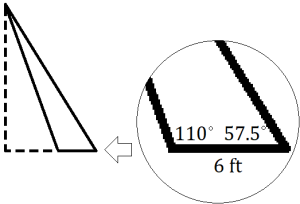
  4. A utility pole is supported by two guy wires as shown in the figure below. The shorter wire makes a 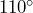110^\circ angle with the sidewalk, the longer wire makes a 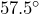57.5^\circ angle with the sidewalk, and the wires meet the sidewalk a distance of 6 feet from each other. Determine the approximate length of each wire.
    a tall narrow obtuse triangle with a 110 degree angle at the bottom left, a 57.5 degree angle at the bottom right, and a bottom side labeled 6 feet

When we need to determine an angle measure, we sometimes have a situation with two possible results: the angle could be acute or obtuse. (For this ambiguous situation to arise, we must know the lengths of two sides and the measure of an acute angle that is not between those two sides.) The inverse sine function on a calculator will always be programmed to give an acute angle measure for the result. If it is clear that the angle should be obtuse, simply subtract the calculator’s result from 180 degrees.

Exercises

Determine the unknown angle measure in each triangle.

  1. Assume that n represents an acute angle.
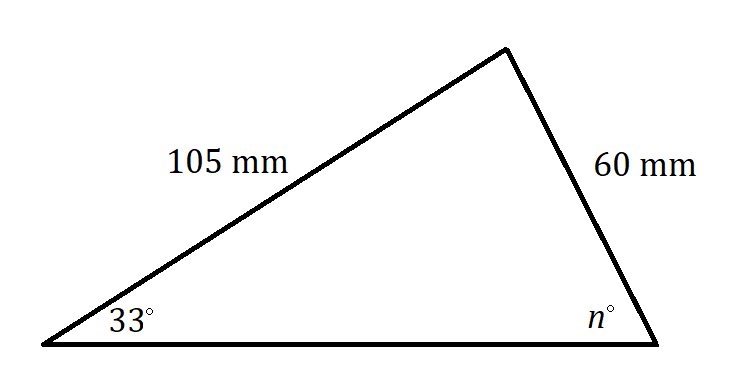
    triangle labeled from the bottom left going counterclockwise: angle marked 33 degrees, unmarked horizontal side, acute angle marked n degrees, side 60 mm, unmarked angle, side 105 mm.
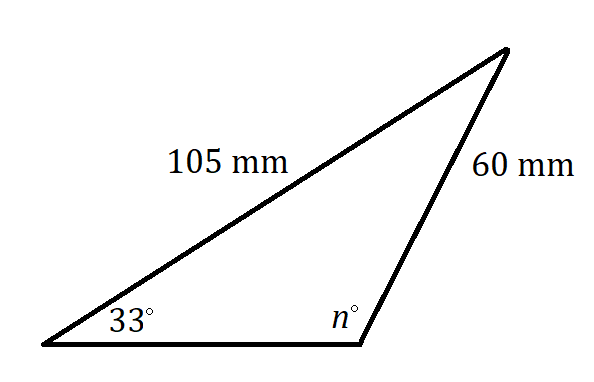
  2. Assume that n represents an obtuse angle.
    triangle labeled from the bottom left going counterclockwise: angle marked 33 degrees, unmarked horizontal side, obtuse angle marked n degrees, side 60 mm, unmarked angle, side 105 mm.

Law of Cosines

Again, suppose we have a triangle with its vertices labeled A, B, C, and the sides opposite each vertex labeled a, b, and c.

right triangle with acute angle A opposite side a, acute angle B opposite side b, and obtuse angle C opposite side c   right triangle with acute angle A opposite side a, acute angle B opposite side b, and acute angle C opposite side c

 

The Law of Cosines is useful when you are dealing with three sides and one angle; if you know three of those values, you can use the formula to figure out the fourth value.

If you’re trying to determine one of the side lengths, use this version.

c=\sqrt{a^2+b^2-2ab\text{ cos }C}

If you’re trying to determine an angle measure, use this version.

C=\text{cos}^{-1}\left(\frac{a^2+b^2-c^2}{2ab}\right)

In either case, the side you name c must be opposite the angle you name C.

Exercises

Determine the unknown value in each triangle.
  1. acute triangle with a 47.3 degree angle at the left, formed by an 87 mm side and a 72 mm side, with the third side marked d.
  2. acute triangle with a 45 degree angle at the lower right, formed by a 16.0 cm side and a 13.0 cm side, with the third side marked p.
  3. obtuse triangle with a 108 degree angle at the top, formed by a 10.47 m side and a 6.78 m side, with the third horizontal side marked w.

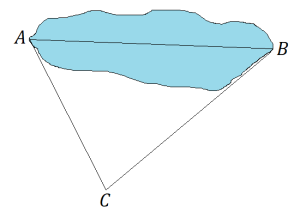
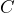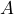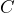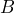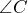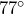  1. Amateur surveyors have determined that the distance from C to A is 53 meters, the distance from C to B is 75 meters, and the measure of \angle C is 77^\circ, as shown in the figure below. What is the length of the pond?

    acute triangle ABC with a pond between endpoints A and B

  2. Determine the measure of each angle.

    triangle labeled from the upper left going counterclockwise: acute angle X, side 11.0 cm, obtuse angle Y, side 8.0 cm, acute angle Z, side 17.5 cm.

Exercise Answers

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Technical Mathematics, 2nd Edition Copyright © 2024 by Morgan Chase is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.