Slope

Bob Brown; Morgan Chase

32 Slope

Bob Brown and Morgan Chase

two houses built on a street that slopes down to the left — This section of Kearney Street in San Francisco is too steep for a sidewalk and has stairs instead. Photo by Marcus Lenk on Unsplash.

You may use a calculator throughout this module.

The slope of a surface is a measure of its steepness. In some cases, such as a walkway or ramp or street, a shallow slope is safer than a steep slope. In other cases, such as a roof, a steep slope may be preferred because it allows rainwater or accumulated snow to move off the roof surface more easily than a shallow slope.^[1]

We will first look at slope in terms of vertical and horizontal distances, and we will then look at slope in terms of angles. Come on, let’s hit the slopes!

Slope as a Ratio

Slope is defined as the ratio of the vertical rise to the horizontal run.

a right triangle with southwest angle marked, south leg marked 'horizontal run' and east leg marked 'vertical rise (positive)' another right triangle with southeast angle marked, south leg marked 'horizontal run' and west leg marked 'vertical rise (negative)'; marked angle below a dashed line that extends horizontally east from northwest corner of triangle

$\text{slope}=\frac{\text{vertical rise}}{\text{horizontal run}}$

A line that is increasing in height has a positive slope.
A line that is decreasing in height has a negative slope.^[2]
The slope of a horizontal line is 0; it is not increasing or decreasing.

A slope may be expressed as a ratio, a decimal, or a percent grade. For example, consider this loading ramp with a vertical rise of 23.5 inches and a horizontal run of 132 inches.

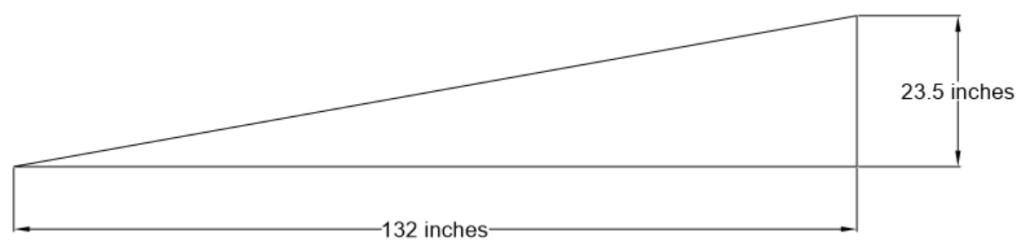
As a ratio, the slope is 23.5 : 132. Dividing the rise by the run gives a decimal value of approximately 0.18. Moving the decimal point two places to the right gives a grade of approximately 18%.

Exercises

Express each slope in three ways: as a ratio, a decimal, and a percent grade.

(This is the preferred maximum slope for sidewalks.)
(This is the maximum allowed slope for sidewalks.)^[3]
(This is the maximum allowed slope for ADA-accessible ramps.)^[4]
(This is the preferred maximum slope for open pit mines.)

Slope as an Angle

The steepness of a line may also be described by its angle of elevation above the horizontal (or its angle of depression below the horizontal).

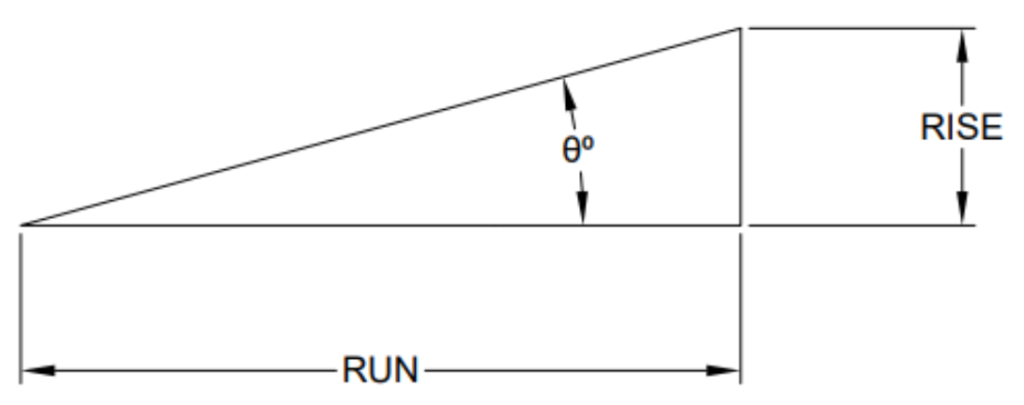
right triangle with southwest angle marked theta, south horizontal leg marked 'run' and east vertical leg marked 'rise'

Notice that the vertical rise is the side opposite the angle, and the horizontal run is the side adjacent to the angle. Therefore, trigonometry tells us that $\text{tangent}=\frac{\text{opposite}}{\text{adjacent}}=\frac{\text{rise}}{\text{run}}$ . The tangent of the angle is equal to the slope.

$\text{tan }\theta=\frac{\text{rise}}{\text{run}}$

Or, thinking about it in reverse, the inverse tangent of the slope is the angle.

$\text{tan}^{-1}\left(\frac{\text{rise}}{\text{run}}\right)=\theta$

Exercises

Determine the angle of elevation for each slope. Round to the nearest hundredth of a degree.

For proper drainage, the ground around a building should slope downwards, away from the building.

The minimum downward grade of the ground is 1%. Assuming this grade, if a point on the ground is 50 feet horizontally from the base of the house, how much lower is the ground at that point?
The preferred minimum downward grade of the ground is 2%. Assuming this grade, if a point on the ground is 50 feet horizontally from the base of the house, how much lower is the ground at that point?
The maximum acceptable downward grade of the ground is 10%. Assuming this grade, if a point on the ground is 50 feet horizontally from the base of the house, how much lower is the ground at that point?

A motion sensor needs to be installed on the outside of a warehouse door 12 feet above the ground. The sensor should go off if anyone approaching the warehouse gets within 20 feet of the door. What angle from vertical should the sensor point away from the building to detect someone at the appropriate distance from the warehouse? Round your answer to the nearest degree.
A ramp is being constructed to the entrance to a public building that is 2.5 feet higher than the level courtyard in front of the entrance. Assuming that the ramp will be continuous with no switchbacks or level platforms,^[5] what is the minimum horizontal distance required for the ramp so that it will comply with ADA regulations?

man with white beard in wheelchair on paved forest path — Photo by Forest Service Pacific Northwest Region on flickr.

Exercise Answers

Source: https://www.nachi.org/roof-slope-pitch.htm ↵
We won't worry about negative slopes in this textbook, because we can always express a negative slope using a word like "decrease", "decline", or "depression" in combination with a positive number. ↵
Source: https://www.ada-compliance.com/ada-compliance/403-walking-surfaces ↵
Source: https://www.ada-compliance.com/ada-compliance/405-ramps ↵
If you were curious, this is the maximum rise allowed for this situation; a rise of more than 2.5 feet would require a switchback or a level platform. ↵

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License