31 Right Triangle Trigonometry
Bob Brown and Morgan Chase

You may use a calculator throughout this module.
The word “trigonometry” essentially means the measurement of triangles. In this module, we will focus on right triangles. If we know some information about a right triangle, such as the measure of one side and one angle, we can use trigonometry to determine the measure of another side.
Sine, Cosine, Tangent
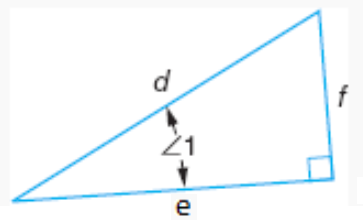
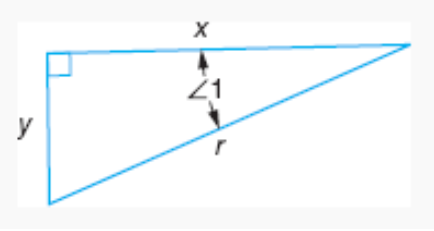
Consider one of the acute angles in a right triangle.
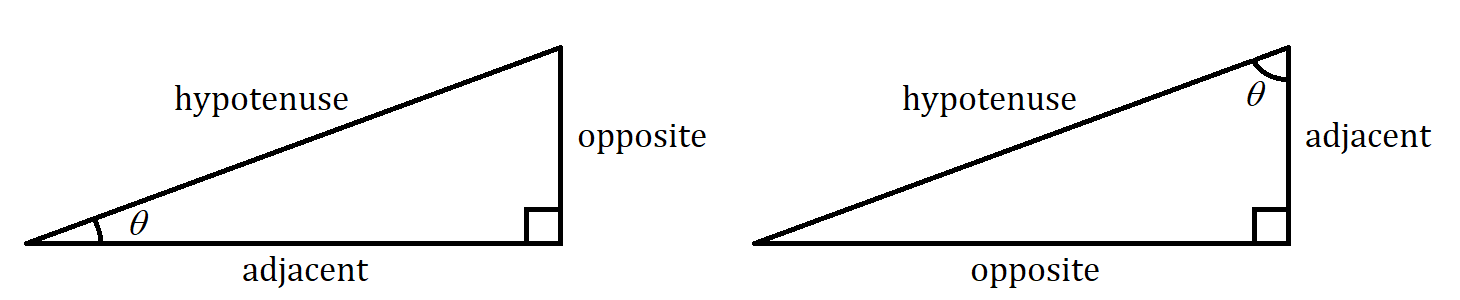
- The sine of the angle is the ratio of the opposite side to the hypotenuse.
- The cosine of the angle is the ratio of the adjacent side to the hypotenuse.
- The tangent of the angle is the ratio of the opposite side to the adjacent side.
Exercises
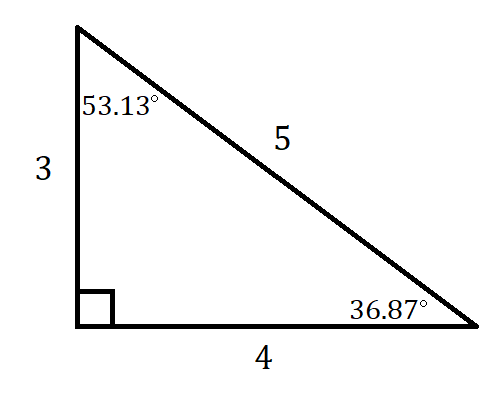
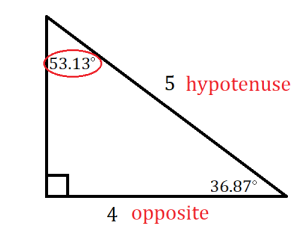
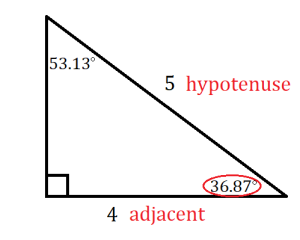
Now let’s look at a specific example, a right triangle with sides of length 3, 4, and 5. Measuring the angles with a protractor will show us that the smaller acute angle is approximately ![]() and the larger acute angle is
and the larger acute angle is ![]() ; to the nearest hundredth of a degree, these values are
; to the nearest hundredth of a degree, these values are ![]() and
and ![]() .
.
Exercises
- sin
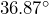
- cos
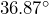
- tan
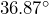
- sin
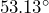
- cos
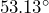
- tan
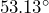
Note that we would have gotten the same results for any right triangle whose sides are in the ratio 3:4:5. If the sides had been 6, 8, 10, the angles measures would still be ![]() and
and ![]() . If the sides had been 30, 40, 50, the angles measures would still be
. If the sides had been 30, 40, 50, the angles measures would still be ![]() and
and ![]() .
.
Or to look at it another way, any right triangle with angles ![]() and
and ![]() will have these relationships: the shorter leg is
will have these relationships: the shorter leg is ![]() the hypotenuse, the longer leg is
the hypotenuse, the longer leg is ![]() the hypotenuse, and the shorter leg is
the hypotenuse, and the shorter leg is ![]() the longer leg. Your scientific calculator knows this and is programmed with all the trigonometric values you need.
the longer leg. Your scientific calculator knows this and is programmed with all the trigonometric values you need.
Exercises
Use your calculator to determine each of the following as a decimal (rounded to four significant figures, if necessary). Be sure that your calculator is in degree mode, not radian mode, before you begin.
- sin
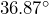
- cos
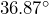
- tan
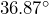
- sin
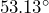
- cos
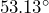
- tan
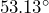
You may notice some repeated answers here, which makes sense because, for example, the side opposite the ![]() angle is adjacent to the
angle is adjacent to the ![]() angle, which means that sin
angle, which means that sin ![]() must be equal to cos
must be equal to cos ![]() .
.
Trigonometry Applications
The sine, cosine, and tangent ratios apply to any right triangle, not just a 3-4-5 triangle, which is what makes trigonometry so useful. If we know the measure of one side and one acute angle in a right triangle, we can use SOHCAHTOA to find the length of another side of the triangle. For each of the following exercises, we’ll need to decide whether the parts we’re dealing with will require us to use sine, cosine, or tangent.
Exercises
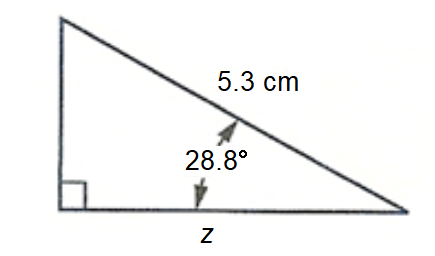
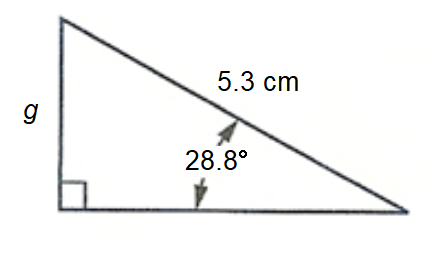
Determine the length of the labeled unknown side of each right triangle. Round each answer appropriately.
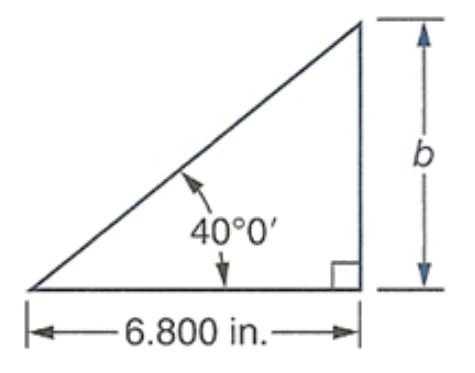
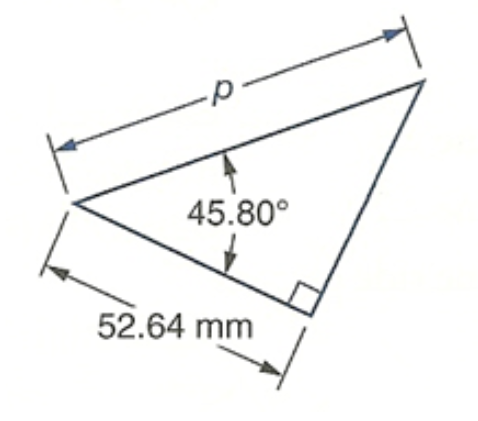
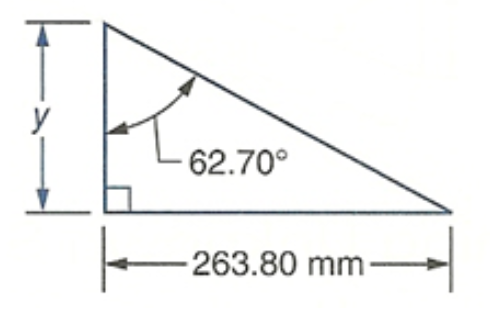
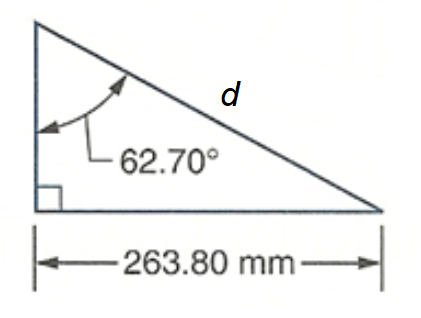
- A guy wire is attached to a utility pole. The wire is anchored to the ground 15 feet from the base of the pole, forming a
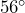 angle with the level ground. What is the length of the wire, to the nearest foot?
angle with the level ground. What is the length of the wire, to the nearest foot? - A 19-foot ladder is leaning against a wall, forming a
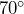 angle with the level ground. What is the vertical height of the place where the ladder contacts the wall?
angle with the level ground. What is the vertical height of the place where the ladder contacts the wall? - During intermission of a hockey game, one lucky fan gets to shoot a puck from the blue line at the goal, 64 feet away, for the chance to win a team jersey. Actually, there is a sheet of fabric blocking the entire goal except for a 6-inch wide hole in the bottom center. If the fan shoots the puck hard enough, aiming directly at the center of the hole, they win. If their aim is off by
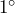 , will they still win the jersey? (If it helps, a hockey puck is 3 inches in diameter.)
, will they still win the jersey? (If it helps, a hockey puck is 3 inches in diameter.)

Inverse Sine, Inverse Cosine, Inverse Tangent
Okay, we now know how to find the length of a side if we know an angle and another side. But what if we know the lengths of the sides and want to determine a missing angle? Rather than carefully making a scale drawing and using a protractor, we can use a calculator.
Your calculator’s SIN, COS, and TAN keys take an angle measure for the input and give a ratio (in decimal form) as the output. Your calculator’s ![]() ,
, ![]() , and
, and ![]() keys allow you to work backwards; they take a ratio for the input and give an angle measure for the output.
keys allow you to work backwards; they take a ratio for the input and give an angle measure for the output.
Exercises
Use your calculator to determine each of the following angle measures (rounded to the nearest hundredth of a degree, if necessary).
Inverse Trigonometry Applications
Exercises
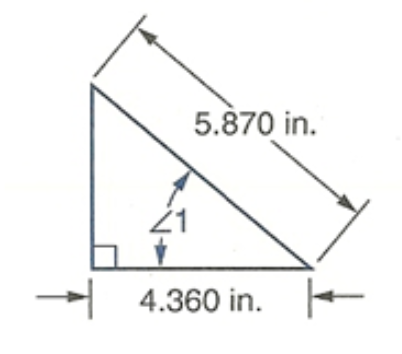
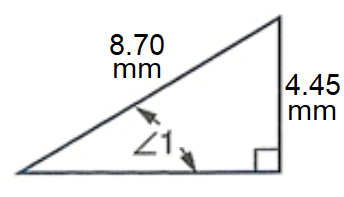
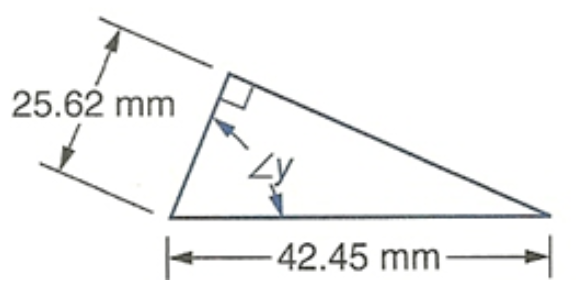
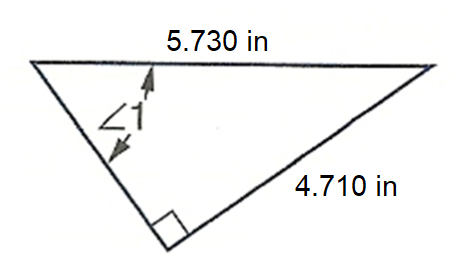
Determine the measure of the marked angle. Round each answer to the nearest hundredth of a degree.
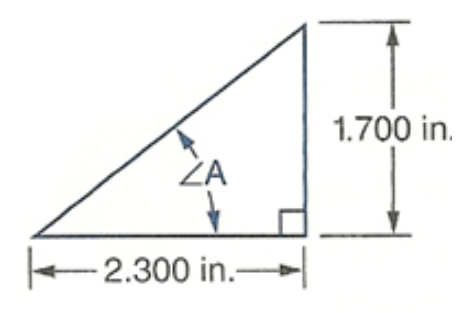
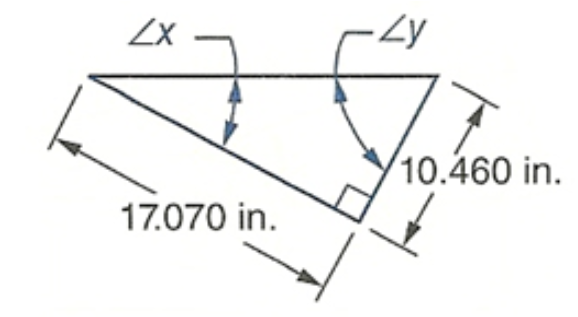
- A rule of thumb for ladder safety is that the vertical height where the ladder touches the wall should be four times the horizontal distance from the base of the ladder to the wall.[1] To the nearest degree, what is the angle between the ladder and the floor in this scenario?
- The entrance to a public building is 2 feet higher than the courtyard in front of the entrance. A ramp is being constructed, continuous with no switchbacks or level platforms, with a surface length of 25 feet. ADA regulations[2] limit the angle of elevation to a maximum of approximately
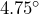 . Does the ramp’s design meet ADA standards?
. Does the ramp’s design meet ADA standards?

Using Multiple Methods
In Module 18, we used the Pythagorean Theorem, ![]() , to determine the length of an unknown side in a right triangle. We can use the Pythagorean Theorem in conjunction with trigonometry to solve a problem in more than one way or to double-check our results.
, to determine the length of an unknown side in a right triangle. We can use the Pythagorean Theorem in conjunction with trigonometry to solve a problem in more than one way or to double-check our results.
Exercises
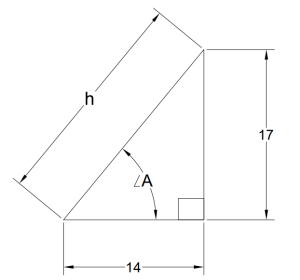
- First, use inverse tangent to determine the value of
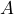 . Round to the nearest tenth of a degree.
. Round to the nearest tenth of a degree. - Next, use sine with
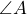 to determine the value of
to determine the value of 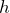 . Round to the nearest tenth.
. Round to the nearest tenth. - Next, use cosine with
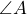 to determine the value of
to determine the value of 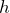 . Round to the nearest tenth.
. Round to the nearest tenth. - Finally, use the Pythagorean Theorem to determine the value of
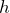 . Round to the nearest tenth.
. Round to the nearest tenth. - Compare your answers for Exercises 36-38. Are they the same or are they different?

- The Wallowa Lake Tramway in Eastern Oregon carries passengers along a
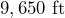 cable, with a vertical rise of
cable, with a vertical rise of 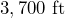 . Although the cable is not straight along its entire length, let’s assume that it is. To the nearest degree, what is the angle of elevation of the cable?
. Although the cable is not straight along its entire length, let’s assume that it is. To the nearest degree, what is the angle of elevation of the cable? - What is the approximate horizontal run covered by the tramway cable?

- Source: https://www.americanladderinstitute.org/page/Ladders101 ↵
- This is implied at https://www.ada-compliance.com/ada-compliance/ada-ramp but not directly stated. We'll verify this angle measure in the next module. ↵