8 Perimeter and Circumference
You may use a calculator throughout this module if needed.
Perimeter
A polygon is a closed geometric figure with straight sides. Common polygons include triangles, squares, rectangles, parallelograms, trapezoids, pentagons, hexagons, octagons… Just as a perimeter fence runs along the outside edge of a region, the perimeter of a polygon is the total distance around the outside. In general, to find the perimeter of a polygon, you can add up the lengths of all of its sides.
Also, if you haven’t already, now is the time to get in the habit of including units in your answers.
Exercises
- Find the perimeter of the triangle.
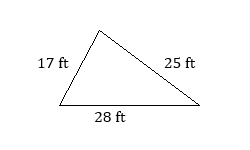
- Find the perimeter of the trapezoid.
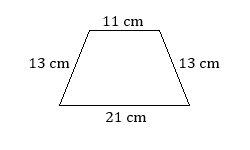
If we know that some of the sides of a polygon are equal, we can use a formula as an alternative to adding up all of the lengths individually. The first formula shown below uses the variable 
for the side of a square. The rectangle formulas use 
for length and 
for width, or 
for base and 
for height; these terms are interchangeable.
Perimeter Formulas
Square: 
Rectangle: 
or 
Rectangle: 
or 
Exercises
- Find the perimeter of the square.
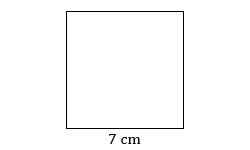
- Find the perimeter of the rectangle.
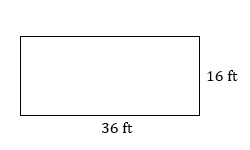
- A storage area, which is a rectangle that is
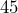feet long and 
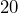feet wide, needs to be fenced around all four sides. How many feet of fencing is required? (To keep it simple, ignore any gates or other complications.) - Giancarlo is putting crown molding around the edge of the ceiling of his living room. If the room is a
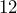-foot by 
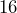-foot rectangle, how much crown molding does he need?
The sides of a regular polygon are all equal in length. Therefore, multiplying the length of a side by the number of sides will give us the perimeter.
Perimeter Formula
Regular Polygon with 
sides of length : 
Exercises
Find the perimeter of each regular polygon.
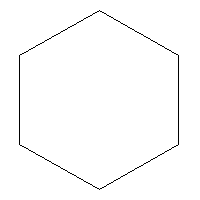
- Each side of the hexagon is
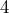inches long.
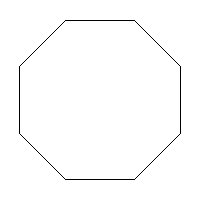
- Each side of the octagon is
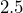centimeters long.
Circumference
The distance around the outside of a circle is called the circumference, rather than the perimeter. Let’s review some circle vocabulary before moving on.
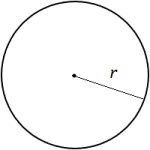
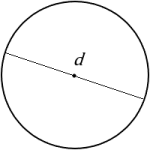
Every point on a circle is the same distance from its center. This distance from the center to the edge of the circle is called the radius. The distance from one edge to another, through the center of the circle, is called the diameter. As you can see, the diameter is twice the length of the radius.
Throughout history, different civilizations have discovered that the circumference of a circle is slightly more than 
times the length of its diameter. (By the year 2000 BCE, the Babylonians were using the value 
and the Egyptians were using the value 
.)[1] The value 
is an even better approximation for the ratio of the circumference to the diameter. However, the actual value cannot be written as an exact fraction; it is the irrational number 
, pronounced “pie”, which is approximately 
.
Circumference Formulas
Any scientific calculator will have a key; using this will give you the most accurate result, although you should be sure to round your answer appropriately. (Remember from Module 5 that we need to pay attention to significant figures when multiplying or dividing.) Many people use 
as an approximation for , but this can lead to round-off error. If you must use an approximation for , use .
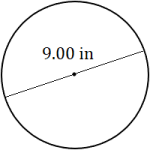
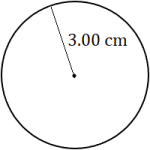
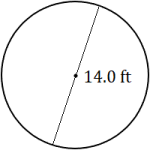
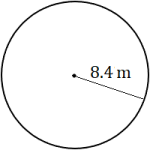
Exercises
Calculate the circumference of each circle. Round each answer to the appropriate level of accuracy.
- This information comes from Chapter 1 of the book A History of Pi by Petr Beckmann. It is a surprisingly interesting read. ↵
a closed geometric figure with straight sides
the distance around the outside of a figure
a figure with all of its sides the same length and all of its angles the same degree measure
the distance around the outside of a circle
the distance from the center to the edge of a circle
the distance across a circle, through the center
