5 Accuracy and Significant Figures

In the first few modules, we rarely concerned ourselves with rounding; we assumed that every number we were told was exact and we didn’t have to worry about any measurement error. However, every measurement contains some error. A standard sheet of paper is ![]() inches wide and
inches wide and ![]() inches high, but it’s possible that the actual measurements could be closer to
inches high, but it’s possible that the actual measurements could be closer to ![]() and
and ![]() inches. Even if we measure something very carefully, with very sensitive instruments, we should assume that there could be some small measurement error.[1]
inches. Even if we measure something very carefully, with very sensitive instruments, we should assume that there could be some small measurement error.[1]
Exact Values and Approximations
A number is an exact value if it is the result of counting or a definition.
A number is an approximation if it is the result of a measurement or of rounding.
Exercises
Identify each number as an exact value or an approximation.
- An inch is
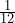 of a foot.
of a foot. - This board is
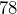 inches long.
inches long. - There are
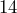 students in class.
students in class. - A car’s tachometer reads
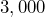 rpm.
rpm. - A right angle measures
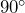 .
. - The angle of elevation of a ramp is
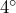 .
.
Accuracy and Significant Figures

Because measurements are inexact, we need to consider how accurate they are. This requires us to think about significant figures—often abbreviated “sig figs” in conversation—which are the digits in the measurement that we trust to be correct. The accuracy of a number is equal to the number of significant figures. (By the way, the terms “significant digits” and “significant figures” are used interchangeably.) The following rules aren’t particularly difficult to understand but they can take time to absorb and internalize, so we’ll include lots of examples and exercises.
Significant Figures
- All nonzero digits are significant.
Ex: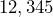 has five sig figs, and
has five sig figs, and 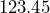 has five sig figs.
has five sig figs. - All zeros between other nonzero digits are significant.
Ex: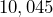 has five sig figs, and
has five sig figs, and 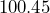 has five sig figs.
has five sig figs. - Any zeros to the right of a decimal number are significant.
Ex: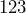 has three sig figs, but
has three sig figs, but 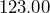 has five sig figs.
has five sig figs. - Zeros on the left of a decimal number are NOT significant.
Ex: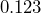 has three sig figs, and
has three sig figs, and 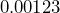 has three sig figs.
has three sig figs. - Zeros on the right of a whole number are NOT significant unless they are marked with an overbar.
Ex: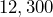 has three sig figs, but
has three sig figs, but 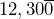 has five sig figs.
has five sig figs.
Another way to think about #4 and #5 above is that zeros that are merely showing the place value—where the decimal point belongs—are NOT significant.
Exercises
Determine the accuracy (i.e., the number of significant figures) of each number.

In 1856, the first official measurement of the height of Mount Everest—called Sagarmatha in Nepal and Chomolungma in Tibet—was announced. The height was determined to be exactly ![]() feet, but there was concern that people would think this was only a rough estimate rounded to the nearest thousand feet. Therefore, the height was announced as
feet, but there was concern that people would think this was only a rough estimate rounded to the nearest thousand feet. Therefore, the height was announced as ![]() feet, so that everyone seeing that number would believe that the measurement was correct to the nearest foot.[2] Yes, to demonstrate the correctness of the measurement, an incorrect measurement was announced.
feet, so that everyone seeing that number would believe that the measurement was correct to the nearest foot.[2] Yes, to demonstrate the correctness of the measurement, an incorrect measurement was announced.
Instead of fudging a number like ![]() to show that it is correct to the nearest foot, we can write it with an an overbar to indicate that the zeros are significant. Putting
to show that it is correct to the nearest foot, we can write it with an an overbar to indicate that the zeros are significant. Putting ![]() in a newspaper headline in 1856 would probably have confused people, but you can handle it because you’re in a math class. Writing
in a newspaper headline in 1856 would probably have confused people, but you can handle it because you’re in a math class. Writing ![]() is our way of saying “Really, to the nearest foot, it’s exactly
is our way of saying “Really, to the nearest foot, it’s exactly ![]() feet!”
feet!”
Exercises
Determine the accuracy (i.e., the number of significant figures) of each number.
Two things to remember: we don’t put an overbar over a nonzero digit, and we don’t need an overbar for any zeros on the right of a decimal number because those are already understood to be significant.
Accuracy-Based Rounding
As we saw in Module 3, it is often necessary to round a number. We often round to a certain place value, such as the nearest hundredth, but there is another way to round. Accuracy-based rounding considers the number of significant figures rather than the place value.
Accuracy-based rounding:
- Locate the rounding digit to which you are rounding by counting from the left until you have the correct number of significant figures.
- Look at the test digit directly to the right of the rounding digit.
- If the test digit is 5 or greater, increase the rounding digit by 1 and drop all digits to its right. If the test digit is less than 5, keep the rounding digit the same and drop all digits to its right.
Exercises
Round each number so that it has the indicated number of significant figures.
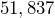 (three sig figs)
(three sig figs)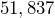 (four sig figs)
(four sig figs)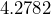 (two sig figs)
(two sig figs)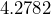 (three sig figs)
(three sig figs)
When the rounding digit of a whole number is a ![]() that gets rounded up to a
that gets rounded up to a ![]() , we must write an overbar above that
, we must write an overbar above that ![]() .
.
Similarly, when the rounding digit of a decimal number is a ![]() that gets rounded up to a
that gets rounded up to a ![]() , we must include the
, we must include the ![]() in that decimal place.
in that decimal place.
Exercises
Round each number so that it has the indicated number of significant figures. Be sure to include trailing zeros or an overbar if necessary.
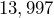 (two sig figs)
(two sig figs)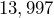 (three sig figs)
(three sig figs)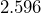 (two sig figs)
(two sig figs)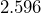 (three sig figs)
(three sig figs)
The height of Mount Everest has changed over the years due to plate tectonics and earthquakes. In December 2020, it was jointly announced by Nepal and China that the summit of Mount Everest has an elevation of ![]() ft.[3]
ft.[3]
- Round
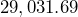 ft to two sig figs.
ft to two sig figs. - Round
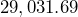 ft to three sig figs.
ft to three sig figs. - Round
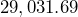 ft to four sig figs.
ft to four sig figs. - Round
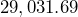 ft to five sig figs.
ft to five sig figs. - Round
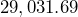 ft to six sig figs.
ft to six sig figs.
Accuracy when Multiplying and Dividing
Suppose you needed to square the number ![]() . You could rewrite
. You could rewrite ![]() as the improper fraction
as the improper fraction ![]() and then figure out that
and then figure out that ![]() , which equals the repeating decimal
, which equals the repeating decimal ![]()
Because most people prefer decimals to fractions, we might decide to round ![]() to
to ![]() and find that
and find that ![]() . The answer
. The answer ![]() looks very accurate, but it is a false accuracy because there is round-off error involved. Only when we round to three sig figs do we get an accurate result:
looks very accurate, but it is a false accuracy because there is round-off error involved. Only when we round to three sig figs do we get an accurate result: ![]() rounded to three sig figs is
rounded to three sig figs is ![]() , which is accurate because
, which is accurate because ![]() rounded to three sig figs is also
rounded to three sig figs is also ![]() . It turns out that because
. It turns out that because ![]() has only three significant figures, our answer must be rounded to three significant figures.
has only three significant figures, our answer must be rounded to three significant figures.
Don’t round off the original numbers; do the necessary calculations first, then round the answer as your last step.
Exercises
Use a calculator to multiply or divide as indicated. Then round to the appropriate level of accuracy.
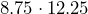
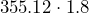
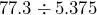
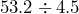
- Suppose you are filling a 5-gallon can of gasoline. The gasoline costs
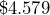 per gallon, and you estimate that you will buy
per gallon, and you estimate that you will buy 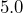 gallons. How much should you expect to spend?
gallons. How much should you expect to spend?
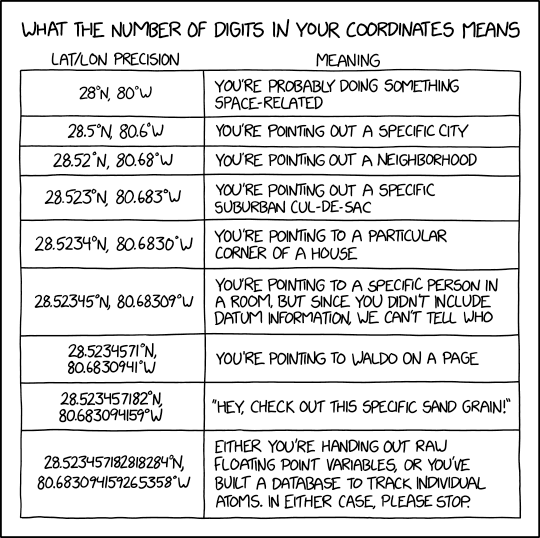
Bonus material: Here is a comic strip from xkcd.com showing that including a lot of decimal digits can give a false sense of accuracy.
- Here is an example of a speed camera with gigantic measurement error: https://youtube.com/shorts/cCYy29RuhV8 ↵
- Source: https://en.wikipedia.org/wiki/Mount_Everest#cite_ref-tas1982_33-0 ↵
- Source: https://www.washingtonpost.com/world/asia_pacific/mount-everest-height-nepal-china/2020/12/08/a7b3ad1e-389a-11eb-aad9-8959227280c4_story.html ↵

