Triangles

Morgan Chase

18 Triangles

Triangular supports hold a boat in the air while it undergoes repairs at the Front Street Shipyard in Belfast, Maine.

Classifying Triangles

We can classify triangles into three categories based on the lengths of their sides.

Equilateral triangle: all three sides have the same length
Isosceles triangle: exactly two sides have the same length
Scalene triangle: all three sides have different lengths

We can also classify triangles into three categories based on the measures of their angles.

Obtuse triangle: one of the angles is an obtuse angle
Right triangle: one of the angles is a right angle
Acute triangle: all three of the angles are acute

Exercises

Classify each triangle by angle and side. For example, “acute scalene”.)

You may use a calculator for the remainder of this module.

Similar Triangles

In one of the diagrams in Module 17, the parallel lines included two similar triangles, although they may be hard to see.

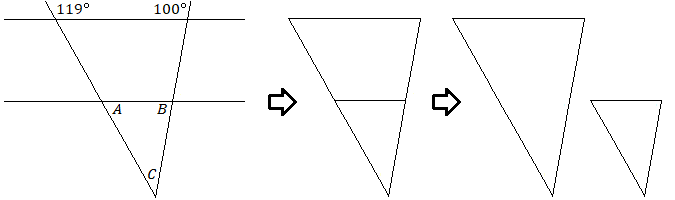
Two triangles are similar if the three angles of one triangle have the same measure as the three angles of the second triangle. The lengths of the sides of similar triangles will be in the same proportion. The triangles will have the same shape but the lengths will be scaled up or down.

Exercises

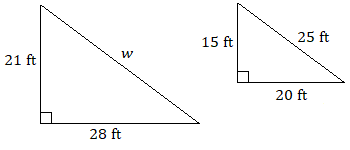
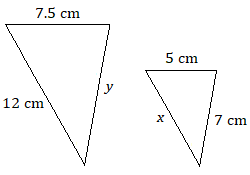
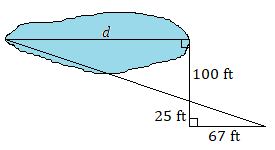
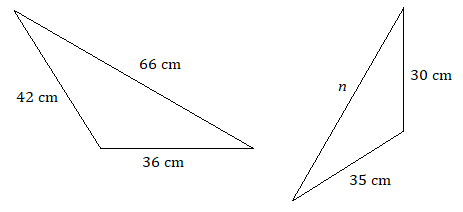
Assume that each pair of triangles are similar. Use a proportion to find each unknown length.

Recognizing corresponding sides can be more difficult when the figures are oriented differently.

Exercises

Assume that each pair of triangles are similar. Use a proportion to find each unknown length.

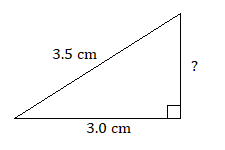
The Pythagorean Theorem

In a right triangle, the two sides that form the right angle are called the legs. The side opposite the right angle, which will always be the longest side, is called the hypotenuse.

The Pythagorean theorem says that the sum of the squares of the lengths of the legs is equal to the square of the length of the hypotenuse.

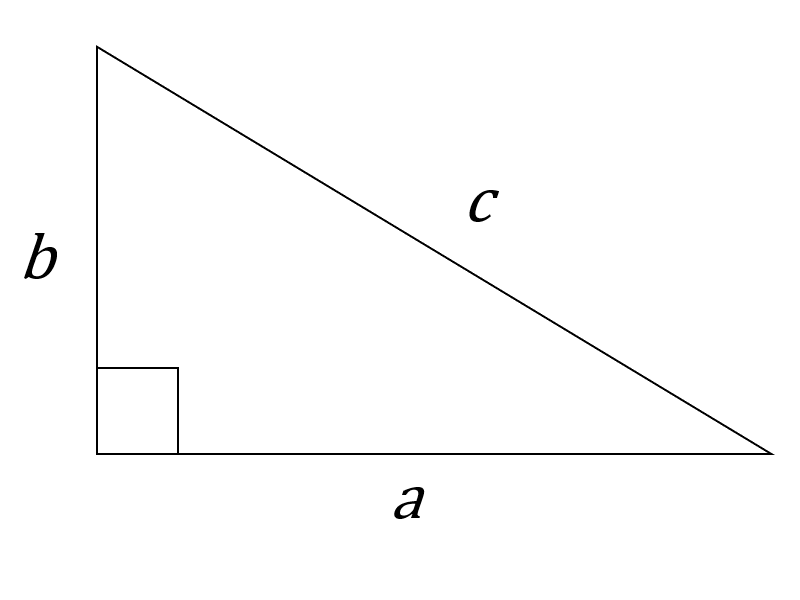
The Pythagorean Theorem

In a right triangle with legs $a$ and $b$ and hypotenuse $c$ ,

$a^2+b^2=c^2$

If you know the lengths of all three sides of a triangle, you can use the Pythagorean theorem to verify whether the triangle is a right triangle or not. The ancient Egyptians used this method for surveying when they needed to redraw boundaries after the yearly flooding of the Nile washed away their previous markings.^[1]

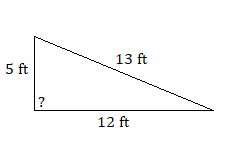
Exercises

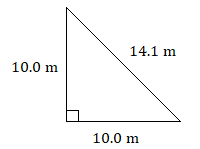
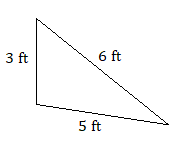
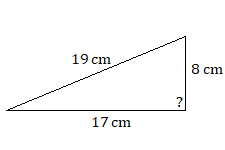
Use the Pythagorean theorem to determine whether either of the following triangles is a right triangle.

Before we continue, we need to briefly discuss square roots. Calculating a square root is the opposite of squaring a number. For example, $\sqrt{49}=7$ because $7^2=49$ . If the number under the square root symbol is not a perfect square like $49$ , then the square root will be an irrational decimal that we will round off as necessary.

Exercises

Use a calculator to find the value of each square root. Round to the hundredths place.

$\sqrt{50}$
$\sqrt{296}$
$\sqrt{943}$

We most often use the Pythagorean theorem to calculate the length of a missing side of a right triangle. Here are three different versions of the Pythagorean theorem arranged to find a missing side, so you don’t have to use algebra with $a^2+b^2=c^2$ .

The Pythagorean Theorem, three other versions

$c=\sqrt{a^2+b^2}$

$b=\sqrt{c^2-a^2}$

$a=\sqrt{c^2-b^2}$

Exercises

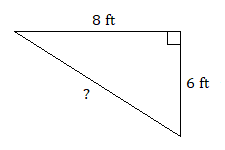
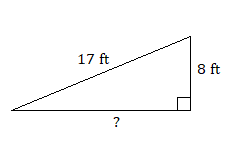
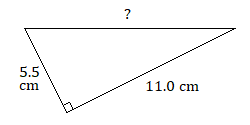
Find the length of the missing side for each of these right triangles. Round to the nearest tenth, if necessary.

Exercise Answers

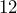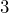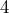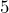The surveyors were called "rope-stretchers" because they used a loop of rope $12$ units long with $12$ equally-spaced knots. Three rope-stretchers each held a knot, forming a triangle with lengths $3$ , $4$ , and $5$ units. When the rope was stretched tight, they knew that the angle between the 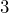$3$ -unit and 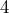$4$ -unit sides was a right angle because 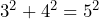$3^2+4^2=5^2$ . From Discovering Geometry: an Inductive Approach by Michael Serra, Key Curriculum Press, 1997. ↵

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License