4 Fractions

Working with fractions is one of the most hated/feared/avoided topics in lower-level mathematics. If you’ve always struggled with fractions, now is the time to face them. Don’t avoid them and hope they’ll go away. (They won’t.) We’ll start with the basics of what fractions are and proceed from there.
Writing Fractions
A fraction describes equal parts of a whole: ![]()
Using official math vocabulary: ![]()
Exercises
The month of April had ![]() rainy days and
rainy days and ![]() days that were not rainy.
days that were not rainy.
- What fraction of the days were rainy?
- What fraction of the days were not rainy?
Simplifying Fractions
Two fractions are equivalent if they represent the same number. (The same portion of a whole.) To build an equivalent fraction, multiply the numerator and denominator by the same number.
Exercises
- Write
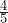 as an equivalent fraction with a denominator of
as an equivalent fraction with a denominator of 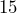 .
. - Write
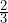 as an equivalent fraction with a denominator of
as an equivalent fraction with a denominator of 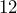 .
.
Many fractions can be simplified, or reduced. Here are four special cases.
Exercises
Simplify each fraction, if possible.
A fraction is completely reduced, or in simplest form, or in lowest terms, when the numerator and denominator have no common factors other than ![]() . To reduce a fraction, divide the numerator and denominator by the same number.
. To reduce a fraction, divide the numerator and denominator by the same number.
Exercises
Reduce each fraction to simplest form.
Multiplying Fractions
To multiply fractions, multiply the numerators and multiply the denominators straight across. If possible, simplify your answer.
Exercises
Multiply each pair of numbers. Be sure that each answer is in simplest form.
To find a fraction of a number, multiply.
Exercises
- To pass his workplace training, Nathan must correctly answer at least
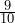 of
of 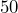 questions. How many questions must he answer correctly to pass the training?
questions. How many questions must he answer correctly to pass the training?
Dividing Fractions
To divide by a fraction, multiply by the reciprocal of the second number. (Flip the second fraction upside-down.)
Exercises
Divide. Be sure that each answer is in simplest form.
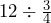
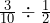
- Suppose you need to measure
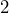 cups of flour, but the only scoop you can find is
cups of flour, but the only scoop you can find is 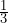 cup. How many scoops of flour will you need?
cup. How many scoops of flour will you need?
Comparing Fractions
If two fractions have the same denominator, we can simply compare their numerators.
If two fractions have different denominators, we can rewrite them with a common denominator and then compare their numerators.
Exercises
- Banana bread recipe A requires
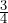 cup of sugar, whereas banana bread recipe B requires
cup of sugar, whereas banana bread recipe B requires 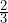 cup of sugar. Which recipe requires more sugar?
cup of sugar. Which recipe requires more sugar?

Adding & Subtracting Fractions
To add or subtract two fractions with the same denominator, add or subtract the numerators and keep the common denominator.
Exercises
- Jack ate
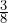 of a pizza. Mack ate
of a pizza. Mack ate 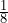 of the pizza. What fraction of the pizza did they eat together?
of the pizza. What fraction of the pizza did they eat together? - Tracy ate
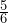 of a pizza. Stacy ate
of a pizza. Stacy ate 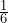 of the pizza. How much more of the pizza did Tracy eat?
of the pizza. How much more of the pizza did Tracy eat?
To add or subtract two fractions with different denominators, first write them with a common denominator. Then add or subtract them.
Exercises
A ![]() -inch thick sheet of plywood is going to be laid onto a
-inch thick sheet of plywood is going to be laid onto a ![]() -inch thick sheet of plywood.
-inch thick sheet of plywood.
- What is the combined thickness of the two sheets?
- What is the difference in thickness of the two sheets of plywood?
Jacqueline budgets ![]() of her monthly income for food and
of her monthly income for food and ![]() of her monthly income for rent.
of her monthly income for rent.
- What fraction of her monthly income does she budget for these two expenses combined?
- What fraction more of her monthly income does she budget for her rent than for her food?
Fractions and Decimals
To write a fraction as a decimal, divide the numerator by the denominator.
A decimal that ends (eventually has a remainder of ![]() ) is called a terminating decimal. Fun fact: If the denominator of a fraction has no prime factors other than
) is called a terminating decimal. Fun fact: If the denominator of a fraction has no prime factors other than ![]() ‘s and
‘s and ![]() ‘s, the decimal will terminate. Also, the fraction can be built up to have a denominator of
‘s, the decimal will terminate. Also, the fraction can be built up to have a denominator of ![]() , or
, or ![]() , or
, or ![]() …
…
Exercises
Write each fraction as a decimal.
A decimal that continues a pattern of digits is called a repeating decimal. We can represent the repeating digits by using either an overbar or ellipsis (three dots)…
Exercises
Write each fraction as a decimal.
Improper Fractions & Mixed Numbers
A fraction which has a larger numerator than denominator is called an improper fraction. Because an improper fraction is larger than ![]() , it can also be written as a mixed number, with a whole number followed by a fractional part.
, it can also be written as a mixed number, with a whole number followed by a fractional part.
Keep in mind that a mixed number represents an addition, not a multiplication. For example, ![]() means
means ![]() , not
, not ![]() .
.
To write an improper fraction as a mixed number:
- Divide the numerator by the denominator to get the whole number part.
- The remainder after dividing is the new numerator.
- Keep the same denominator.
Exercises
Rewrite each improper fraction as a mixed number.
To write a mixed number as an improper fraction:
- Multiply the whole number part by the denominator.
- Add this result to the original numerator to get the new numerator.
- Keep the same denominator.
Exercises
Rewrite each mixed number as an improper fraction.
Adding or subtracting mixed numbers can be fairly simple or more complicated, depending on the numbers. One approach is to work with the fractional parts separately from the whole numbers. For example, ![]() can be rewritten as
can be rewritten as ![]() and rearranged to
and rearranged to ![]() . Then
. Then ![]() and, with a little more work,
and, with a little more work, ![]() , so the result is
, so the result is ![]() .
.
Exercises
Multiplying or dividing mixed numbers is more complicated than it may appear. Change any mixed numbers into improper fractions before doing the calculation, then change the answer back to a mixed number if possible.
Exercises
- Multiply:
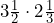
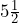 cups of water will be divided equally into
cups of water will be divided equally into 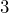 jars. How much water will go into each jar?
jars. How much water will go into each jar?

