10 Ratios, Rates, Proportions

As we saw in the previous module, a percent is a fraction that compares a number to 100. This is an example of a ratio. In this module, we will focus on ratios and rates, which look like fractions, and then we’ll finish up with proportions, which look like two fractions set equal to each other. Many of the examples in this module can be worked without a calculator, while others are best done with a calculator because you’ll be multiplying big numbers or dividing messy decimals. You can ask your instructor for guidance if you aren’t sure whether a calculator is appropriate.

Ratios & Rates

A ratio is the quotient of two numbers or the quotient of two quantities with the same units. (Pop quiz… Which operation gives you a quotient: addition, subtraction, multiplication, or division?)

When writing a ratio as a fraction, the first quantity is the numerator and the second quantity is the denominator. If the fraction can be simplified, reduce it to lowest terms.

Exercises

  1. Find the ratio of 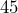45 minutes to 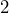2 hours. Simplify the fraction, if possible.

A rate is the quotient of two quantities with different units. You must include the units.

When writing a rate as a fraction, the first quantity is the numerator and the second quantity is the denominator. If the fraction can be simplified, reduce it to lowest terms.

Exercises

  1. A car travels 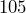105 miles in 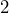2 hours. Write the rate as a fraction.

Unit Rates

For practical purposes, expressing a rate as a reduced fraction is not always useful. Expressing a rate as a single number with units such as miles per hour is often more meaningful. This is called a unit rate because it expresses the quantity in the numerator that corresponds to one unit of the denominator.

To find the unit rate, divide the numerator by the denominator and express the rate as a mixed number or decimal. The units can be expressed with the word “per”: miles per hour, dollars per gallon, grams per deciliter, pounds per square inch, and so on.

Exercises

  1. A car travels 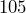105 miles in 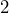2 hours. Write the car’s average speed as a unit rate.

A unit price is a rate with the price in the numerator and a denominator equal to 1. The unit price tells the cost of one unit or one item. To find the unit price, divide the cost by the size or number of items.

You may use a calculator to calculate the unit price.

Exercises

  1. A 15.8-ounce box of Carmella Creeper cereal costs $5.29. Determine the unit price.
  2. An 18.8-ounce box of Count Chocula cereal costs $5.29. Determine the unit price.
  3. The Monster Cereals are on sale, 2 boxes for $9. If you buy a 16-ounce box of Franken Berry cereal and a 16-ounce box of Boo Berry cereal, what is the unit price per ounce?

Proportions

A proportion says that two ratios (or rates) are equal.

Exercises

Determine whether each proportion is true or false by simplifying each fraction.

  1. \frac{6}{8}=\frac{21}{28}
  2. \frac{10}{15}=\frac{16}{20}

A common method of determining whether a proportion is true or false is called cross-multiplying or finding the cross products. We multiply diagonally across the equal sign. In a true proportion, the cross products are equal.

\frac{a}{b}=\frac{c}{d}  →   {a}\cdot{d}={b}\cdot{c}

Exercises

Determine whether each proportion is true or false by cross-multiplying.

  1. \frac{6}{8}=\frac{21}{28}
  2. \frac{10}{15}=\frac{16}{20}
  3. \frac{14}{4}=\frac{15}{5}
  4. \frac{0.8}{4}=\frac{5}{25}

As we saw in Module 7, we can use a variable to stand for a missing number. If a proportion has a missing number, we can use cross multiplication to solve for the missing number. This is as close to algebra as we get in this textbook.

To solve a proportion for a variable:

  1. Set the cross products equal to form an equation of the form {a}\cdot{d}={b}\cdot{c}.
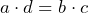  2. Isolate the variable by rewriting the multiplication equation as a division equation.
  3. Check the solution by substituting the answer into the original proportion and finding the cross products.

You may discover slightly different methods that you prefer. If you think “Hey, can’t I do this a different way?”, you’re probably right.

Exercises

Solve for the variable.

  1. \frac{8}{10}=\frac{x}{15}
  2. \frac{3}{2}=\frac{7.5}{n}
  3. \frac{3}{k}=\frac{18}{24}
  4. \frac{w}{6}=\frac{15}{9}
  5. \frac{5}{4}=\frac{13}{x}
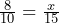
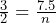
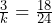
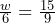
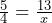
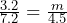  6. \frac{3.2}{7.2}=\frac{m}{4.5} (calculator recommended)

Problems that involve rates, ratios, scale models, etc. can be solved with proportions. When solving a real-world problem using a proportion, be consistent with the units.

You may use a calculator for the remainder of this module if needed.

Exercises

  1. Tonisha drove her car 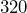320 miles and used 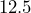12.5 gallons of gas. At this rate, how far could she drive using 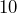10 gallons of gas?
  2. Marcus worked 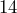14 hours and earned 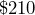\textdollar210. At the same rate of pay, how long would he have to work to earn \textdollar300?
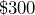  3. Taylor is trying to figure out the straight-line distance from Portland to Mt. Hood. On their map, 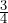\frac{3}{4} inch represents 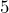5 miles. The distance between Portland and Mt. Hood on the map is pretty close to 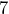7 inches. What is the actual distance?
  4. Púki the cat lives in a Reykjavík bookstore and likes to sleep on a warm tabletop video screen. Suppose you have a picture of Púki that is 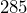285 pixels wide and 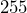255 pixels high but you need to reduce it in size so that it is 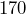170 pixels high. If the height and width are kept proportional, what is the width of the picture after it has been reduced?
    That’s pronounced “pookee”, not “pyookee”.

 

Exercise Answers

definition

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Technical Mathematics, 2nd Edition Copyright © 2024 by Morgan Chase is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.