25 Converting Units of Volume
You may use a calculator throughout this module.

Just as we saw with area, converting between units of volume requires us to be careful because cubic units behave differently than linear units.
Quantities of mulch, dirt, or gravel are often measured by the cubic yard. How many cubic feet are in one cubic yard?
![]() yard =
yard = ![]() feet, so we can divide the length into three sections, the width into three sections, and the height into three sections to convert all three dimensions of the cube from yards to feet. This forms a
feet, so we can divide the length into three sections, the width into three sections, and the height into three sections to convert all three dimensions of the cube from yards to feet. This forms a ![]() by
by ![]() by
by ![]() cube, which shows us that
cube, which shows us that ![]() cubic yard equals
cubic yard equals ![]() cubic feet. The linear conversion ratio of
cubic feet. The linear conversion ratio of ![]() to
to ![]() means that that the conversion ratio for the volumes is
means that that the conversion ratio for the volumes is ![]() to
to ![]() , or
, or ![]() to
to ![]() .
.
Here’s another way to think about it without a diagram: ![]() , so
, so ![]() . To remove the parentheses, we must cube the number and cube the units:
. To remove the parentheses, we must cube the number and cube the units: ![]() .
.
More generally, we need to cube the linear conversion factors when converting units of volume. If the linear units have a ratio of ![]() to
to ![]() , the cubic units will have a ratio of
, the cubic units will have a ratio of ![]() to
to ![]() .
.
U.S. System: Converting Measurements of Volume
![]()
![]()
![]()
Exercises
- True story: A friend at the National Guard base gave us three long wooden crates to use as raised planting beds. (The crates probably carried some kind of weapons or ammunition, but our friend wouldn’t say.) Henry, who was taking geometry in high school, was asked to measure the crates and figure out how much soil we needed. The inside dimensions of each crate were
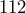 inches long,
inches long, 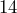 inches wide, and
inches wide, and 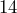 inches deep. We wanted to fill them most of the way full with soil, leaving about
inches deep. We wanted to fill them most of the way full with soil, leaving about 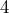 inches empty at the top. How many cubic yards of soil did we need to order from the supplier?
inches empty at the top. How many cubic yards of soil did we need to order from the supplier? - True story, continued: We decided to check our answer and did a rough estimate by rounding each dimension to the nearest foot, then figuring out the volume from there. Did this give the same result?

We can convert between units of volume and liquid capacity. As you might expect, the numbers are messy in the U.S. system.
![]()
![]()
Exercises
- A circular wading pool has a diameter of roughly 5 feet and a depth of 6 inches. How many gallons of water are required to fill it about
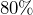 of the way full?
of the way full? - A standard U.S. soda pop can has a diameter of
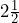 inches and a height of
inches and a height of 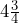 inches. Verify that the can is able to hold
inches. Verify that the can is able to hold 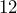 fluid ounces of liquid.
fluid ounces of liquid. - A water jug that is roughly cube-shaped is advertised with dimensions
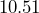 inches deep,
inches deep, 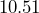 inches wide, and
inches wide, and 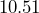 inches high. How many gallons is its capacity?
inches high. How many gallons is its capacity?

Metric System: Converting Measurements of Volume
![]()
![]()
![]()
![]()
![]()
It’s no surprise that the metric conversion ratios for volume are all powers of ![]() … but they are actually powers of
… but they are actually powers of ![]() , or
, or ![]() , because the linear conversions get cubed when we go three-dimensional.
, because the linear conversions get cubed when we go three-dimensional.
Exercises
- The circular soaking tubs at Hot Lake Springs in La Grande, Oregon have an inner diameter of
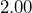 meters, and the water has a depth of
meters, and the water has a depth of 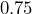 meters. What is the approximate volume of water, in liters, in one of the tubs?
meters. What is the approximate volume of water, in liters, in one of the tubs?

- A
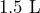 carton of orange juice has a square base
carton of orange juice has a square base 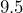 centimeters on each side, and the height of the rectangular section is
centimeters on each side, and the height of the rectangular section is 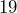 centimeters. (Ignore the triangular section at the top.) Verify that the carton holds
centimeters. (Ignore the triangular section at the top.) Verify that the carton holds 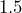 liters of juice.
liters of juice. - A
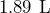 carton of POG juice has a square base
carton of POG juice has a square base 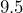 centimeters on each side, and the height of the rectangular section is
centimeters on each side, and the height of the rectangular section is 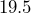 centimeters. This is not enough volume to hold
centimeters. This is not enough volume to hold 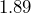 liters of juice unless the sides of the carton bulge out. If you unfold the triangular top section to make a rectangular column and squeeze the sides of the carton so they aren’t bulging out, what height will the juice rise to?
liters of juice unless the sides of the carton bulge out. If you unfold the triangular top section to make a rectangular column and squeeze the sides of the carton so they aren’t bulging out, what height will the juice rise to?

Both Systems: Converting Measurements of Volume
Converting volumes between the U.S. and metric systems will of course involve messy decimal values. For example, because ![]() , we can cube both numbers and find that
, we can cube both numbers and find that ![]()
![]() . The conversions in the table below are rounded to five significant figures.
. The conversions in the table below are rounded to five significant figures.
Exercises
- A large dumpster in Iceland has a volume of
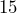 cubic meters. Convert this to cubic yards.
cubic meters. Convert this to cubic yards. - Suppose you need to know the volume of an Icelandic dumpster in cubic feet. Convert
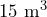 to
to 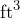 .
.

- A “two yard” dumpster at a campground in Washington has a volume of
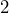 cubic yards. Convert this to cubic meters.
cubic yards. Convert this to cubic meters.

- The engine of a 1964 Corvette has 8 cylinders with a bore (diameter) of
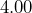 inches and a stroke (height) of
inches and a stroke (height) of 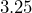 inches. Find the total displacement (volume) of the cylinders in this engine, rounded to the nearest cubic inch.[1]
inches. Find the total displacement (volume) of the cylinders in this engine, rounded to the nearest cubic inch.[1] - Convert the displacement of the Corvette engine into cubic centimeters.
- Convert the displacement of the Corvette engine into liters.

- A hardware store sells pea gravel in
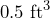 bags. The bags are also marked
bags. The bags are also marked 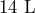 . Verify that these two measures are equivalent.
. Verify that these two measures are equivalent.
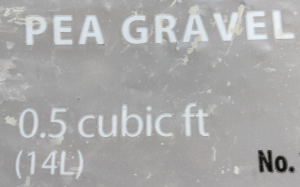
Density
The density of a material is its weight per volume such as pounds per cubic foot, or mass per volume such as grams per cubic centimeter. Multiplying the volume of an object by its density will give its weight or mass.
Exercises
- A
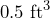 bag of pea gravel weighs approximately 50 pounds. Determine the density of pea gravel in pounds per cubic foot.
bag of pea gravel weighs approximately 50 pounds. Determine the density of pea gravel in pounds per cubic foot. - The standard size of a gold bar in the U.S. Federal Reserve is
 inches by
inches by 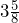 inches by
inches by 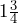 inches.[2] The density of gold is
inches.[2] The density of gold is 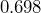 pounds per cubic inch. How much does one gold bar weigh?
pounds per cubic inch. How much does one gold bar weigh? - A cylindrical iron bar has a diameter of
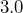 centimeters and a length of
centimeters and a length of 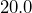 centimeters. The density of iron is
centimeters. The density of iron is 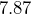 grams per cubic centimeter. What is the bar’s mass, in kilograms?
grams per cubic centimeter. What is the bar’s mass, in kilograms?
Volumes of Similar Solids
Earlier in this module, it was stated that if the linear units have a ratio of ![]() to
to ![]() , the cubic units will have a ratio of
, the cubic units will have a ratio of ![]() to
to ![]() . This applies to similar solids as well.
. This applies to similar solids as well.
We’ll verify this in the following exercises.
Exercises
 A table tennis (ping pong) ball has a diameter of
A table tennis (ping pong) ball has a diameter of ![]() centimeters. A wiffle® ball has a diameter twice that of a table tennis ball.
centimeters. A wiffle® ball has a diameter twice that of a table tennis ball.
- Determine the volume of the wiffle® ball.
- Determine the volume of the table tennis ball.
- What is the ratio of the volumes of the two balls?
Rectangular solid ![]() has dimensions
has dimensions ![]() inches by
inches by ![]() inches by
inches by ![]() inches. Rectangular solid
inches. Rectangular solid ![]() has dimensions triple those of
has dimensions triple those of ![]() ’s.
’s.
- Determine the volume of the larger solid,
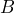 .
. - Determine the volume of the smaller solid,
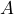 .
. - What is the ratio of the volumes of the two solids?
- The formula is often written as
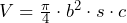 , where
, where  is the number of cylinders. ↵
is the number of cylinders. ↵ - Source: https://www.usmint.gov/about/mint-tours-facilities/fort-knox ↵

