20 Composite Figures
You may use a calculator in this module as needed.
Many objects have odd shapes made up of simpler shapes. A composite figure is a geometric figure which is formed by—or composed of—two or more basic geometric figures.
We will look at a handful of fairly simple examples, but this concept can of course be extended to much more complicated figures.
Composite Figures with Polygons
To find the area of a composite figure, it is generally a good idea to divide it into simpler shapes—rectangles, triangles, etc.—and either add or subtract their areas as necessary. You may need to figure out some unmarked dimensions during the process.
Exercises
A floor plan of a room is shown. The room is a 
-foot by 
-foot rectangle, with a 
-foot by 
-foot rectangle cut out of the south side.
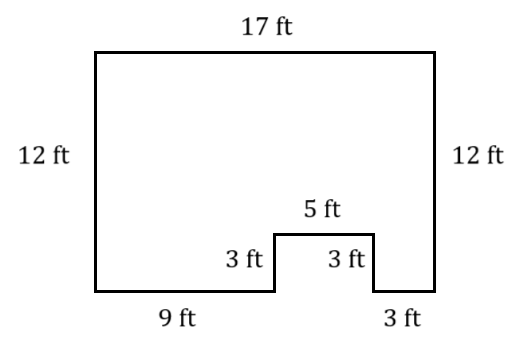
- Determine the amount of molding required for the perimeter of the room.
- Determine the amount of flooring required to cover the entire area.
A trapezoid is formed by removing two right triangles from a rectangle, as shown.
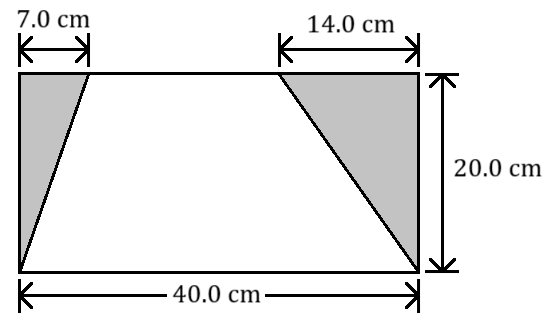
- Determine the area of the trapezoid without using the trapezoid formula from Module 19.
- Determine the area of the trapezoid using the trapezoid formula from Module 19. Does this agree with your previous answer?
A plan for an irregular parking lot is shown.
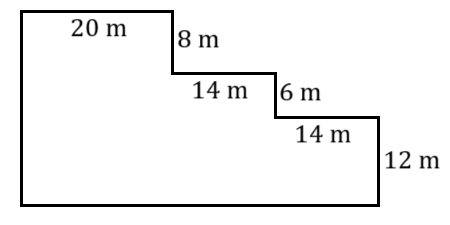
- Calculate the perimeter.
- Calculate the area.
Composite Figures with Circles
If a composite figure includes parts of circles, you’ll need to approximate you answer because your calculation will have 
in it.
Exercises
meters.
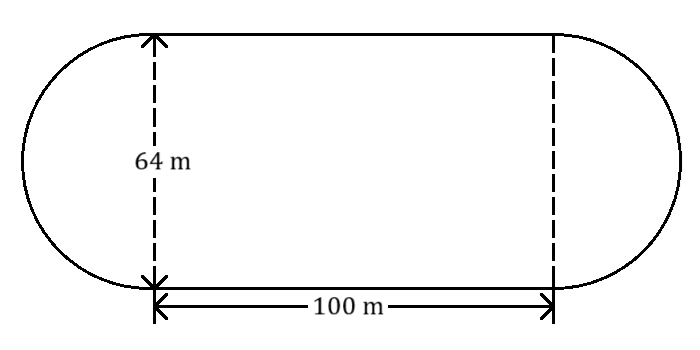
- Determine the distance around the track. Will the track be the right length?
- After the new track is built, landscapers need to lay sod on the field inside the track. What is the area of the field inside the track?
The radius of the quarter circle is 
centimeters.
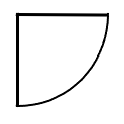
- Calculate the area.
- Calculate the perimeter.
A quarter circle has been removed from a circle with a diameter of 
feet.
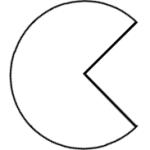
- Calculate the area.
- Calculate the perimeter.
If we need to determine a fraction or percent out of the whole, we may be able to solve the problem without knowing any actual measurements.
Exercises
- Circular disks are being cut from squares of sheet metal, with the remainder around the corners being discarded. Assuming that the circles are made as large as possible, what percent of the sheet metal will be discarded?
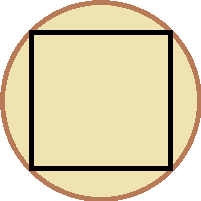
- A log with a circular cross-section is being planed to create a beam with a square cross-section. Assuming that the beam is made as large as possible, what percent of the log will be removed?
