Area of Polygons and Circles

Morgan Chase

19 Area of Polygons and Circles

You may use a calculator in this module as needed.

We have seen that the perimeter of a polygon is the distance around the outside. Perimeter is a length, which is one-dimensional, and so it is measured in linear units (feet, centimeters, miles, etc.). The area of a polygon is the amount of two-dimensional space inside the polygon, and it is measured in square units: square feet, square centimeters, square miles, etc.

You can always think of area as the number of squares required to completely fill in the shape.

Area: Rectangles and Squares

Exercises

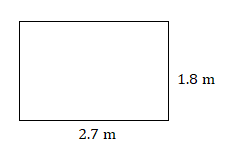
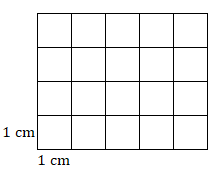
Find the area of this rectangle.
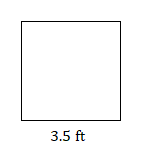
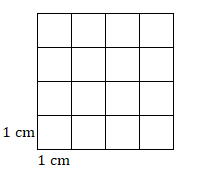
Find the area of this square.

There are of course formulas for finding the areas of rectangles and squares; we don’t have to count little squares.

Area of a Rectangle

$A=lw$ ^[1] or $A=bh$

Area of a Square

$A=s^2$

Exercises

Find the area of each figure.

Area: Parallelograms

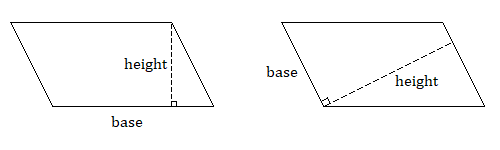
Another common polygon is the parallelogram, which looks like a tilted rectangle. As the name implies, the pairs of opposite sides are parallel and have the same length. Notice that, if we label one side as a base of the parallelogram, we have a perpendicular height which is not the length of the other sides.

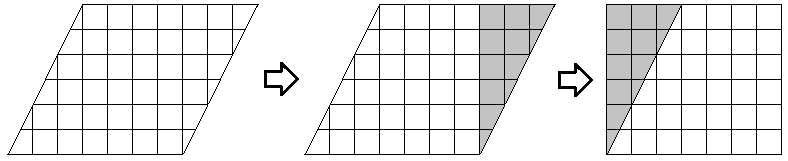
The following set of diagrams shows that we can cut off part of a parallelogram and rearrange the pieces into a rectangle with the same base and height as the original parallelogram. A parallelogram with a base of $7$ units and a vertical height of $6$ units is transformed into a $7$ by $6$ rectangle, with an area of $42$ square units.

Therefore, the formula for the area of a parallelogram is identical to the formula for the area of a rectangle, provided that we are careful to use the base and the height, which must be perpendicular.

Area of a Parallelogram

$A=bh$

Exercises

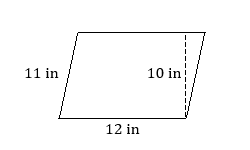
Find the area of each parallelogram.

Area: Triangles

When we are finding the area of a triangle, we need to identify a base and a height that is perpendicular to that base. If the triangle is obtuse, you may have to imagine the height outside of the triangle and extend the base line to meet it.

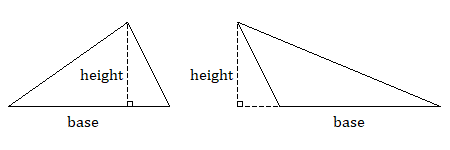
As shown below, any triangle can be doubled to form a parallelogram. Therefore, the area of a triangle is one half the area of a parallelogram with the same base and height.

Area of a Triangle

$A=\frac{1}{2}bh$ or $A=bh\div2$

As with a parallelogram, remember that the height must be perpendicular to the base.

Exercises

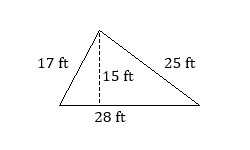
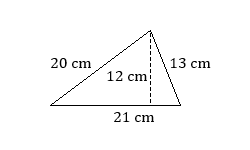
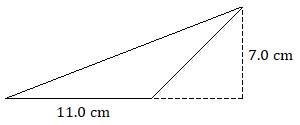
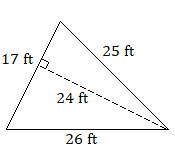
Find the area of each triangle.

Area: Trapezoids

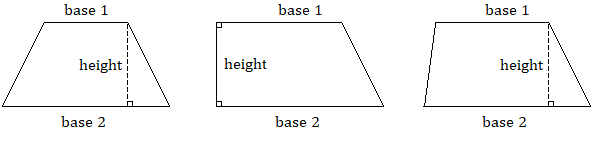
A somewhat less common quadrilateral is the trapezoid, which has exactly one pair of parallel sides, which we call the bases. The first example shown below is called an isosceles trapezoid because, like an isosceles triangle, its two nonparallel sides have equal lengths.

There are a number of ways to show where the area formula comes from, but the explanations are better in video because they can be animated.^[2]^[3]^[4]

Area of a Trapezoid

$A=\frac{1}{2}h(b_1+b_2)$ or $A=(b_1+b_2)h\div2$

Don’t be intimidated by the subscripts on $b_1$ and $b_2$ ; it’s just a way to name two different measurements using the same letter for the variable. (Many people call the bases $a$ and $b$ instead; feel free to write it whichever way you prefer.) Whatever you call them, you just add the two bases, multiply by the height, and take half of that.

Exercises

seven trapezoids arranged in a circle to form a seven-sided polygon

The soaking tubs at Hot Lake Springs in La Grande, Oregon have benches formed by seven trapezoids. Each bench has an outer edge 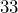$33$ inches long, an inner edge 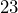$23$ inches long, and the edges are 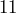$11$ inches apart. How much seating area do the benches provide? (Ignore the gaps between the boards.)

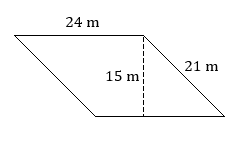
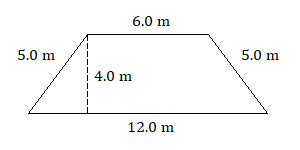
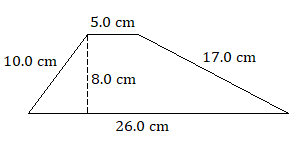
Find the area of each trapezoid.

Rocky the cat lounges at Hot Lake Springs.

Area: Circles

The area of a circle is $\pi$ times the square of the radius: $A=\pi{r^2}$ . The units are still square units, even though a circle is round. (Think of the squares on a round waffle.) Because we can’t fit a whole number of squares—or an exact fraction of squares—inside the circle, the area of a circle will be an approximation.

If your calculator doesn’t have a $\pi$ key, use the approximation $\pi\approx3.1416$ .

Area of a Circle

$A=\pi{r^2}$

Exercises

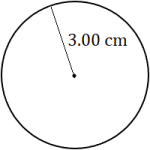
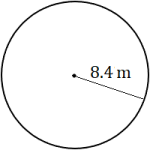
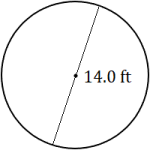
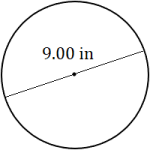
Find the area of each circle. Round each answer to the appropriate number of significant figures.

Exercise Answers

You might choose to use capital letters for the variables here because a lowercase letter "l" can easily be mistaken for a number "1". ↵
https://youtu.be/yTnYRpcZA9c ↵
https://youtu.be/WZtO3oERges ↵
https://youtu.be/uLHc6Br2veg ↵

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License