22 Surface Area of Common Solids
You may use a calculator throughout this module.
We will now turn our attention from two-dimensional figures to three-dimensional figures, which we often call solids, even if they are hollow inside.
In this module, we will look the surface areas of some common solids. (We will look at volume in a later module.) Surface area is what it sounds like: it’s the sum of the areas of all of the outer surfaces of the solid. When you are struggling to wrap a present because your sheet of wrapping paper isn’t quite big enough, you are dealing with surface area.
 There are two different kinds of surface area that are important: the lateral surface area (LSA) and total surface area (TSA).
There are two different kinds of surface area that are important: the lateral surface area (LSA) and total surface area (TSA).
To visualize the difference between LSA and TSA, consider a can of food. The lateral surface area would be used to measure the size of the paper label around the can. The total surface area would be used to measure the amount of sheet metal needed to make the can. In other words, the total surface area includes the top and bottom, whereas the lateral surface area does not.
Surface Area: Rectangular Solids
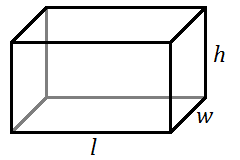
A rectangular solid looks like a rectangular box. It has three pairs of equally sized rectangles on the front and back, on the left and right, and on the top and bottom.
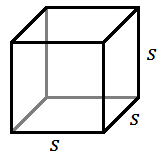
A cube is a special rectangular solid with equally-sized squares for all six faces.
The lateral surface area is the combined total area of the four vertical faces of the solid, but not the top and bottom. If you were painting the four walls of a room, you would be thinking about the lateral surface area.
The total surface area is the combined total area of all six faces of the solid. If you were painting the four walls, the floor, and the ceiling of a room, you would be thinking about the total surface area.
 For a rectangular solid with length
For a rectangular solid with length ![]() , width
, width ![]() , and height
, and height ![]() …
…
![]()
![]()
![]()
 For a cube with side length
For a cube with side length ![]() …
…
![]()
![]()
Note: These dimensions are sometimes called base, depth, and height.
Exercises
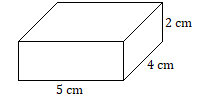
- Find the lateral surface area of this rectangular solid.
- Find the total surface area of this rectangular solid.
Surface Area: Cylinders
 As mentioned earlier in this module, the lateral surface area of a soup can is the paper label, which is a rectangle. Therefore, the lateral surface area of a cylinder is a rectangle; its width is equal to the circumference of the circle,
As mentioned earlier in this module, the lateral surface area of a soup can is the paper label, which is a rectangle. Therefore, the lateral surface area of a cylinder is a rectangle; its width is equal to the circumference of the circle, ![]() , and its height is the height of the cylinder.
, and its height is the height of the cylinder.
Since a cylinder has equal-sized circles at the top and bottom, its total surface area is equal to the lateral surface area plus twice the area of one of the circles.
For a cylinder with radius ![]() and height
and height ![]() …
…
![]()
![]()
![]()
Be aware that if you are given the diameter of the cylinder, you will need to cut it in half before using these formulas.
Exercises
 A cylinder has a diameter of
A cylinder has a diameter of ![]() and a height of
and a height of ![]() .
.
- Find the lateral surface area.
- Find the total surface area.
Surface Area: Spheres
 The final solid of this module is the sphere, which can be thought of as a circle in three dimensions: every point on the surface of a sphere is the same distance from the center. Because of this, a sphere has only one important measurement: its radius. Of course, its diameter could be important also, but the idea is that a sphere doesn’t have different dimensions such as length, width, and height. A sphere has the same radius (or diameter) in every direction.
The final solid of this module is the sphere, which can be thought of as a circle in three dimensions: every point on the surface of a sphere is the same distance from the center. Because of this, a sphere has only one important measurement: its radius. Of course, its diameter could be important also, but the idea is that a sphere doesn’t have different dimensions such as length, width, and height. A sphere has the same radius (or diameter) in every direction.
We would need to use calculus to derive the formula for the surface area of a sphere, so we’ll just assume it’s true and get on with the business at hand. Notice that, because a sphere doesn’t have top or bottom faces, we don’t need to worry about finding the lateral surface area. The only surface area is the total surface area.
For a sphere with radius ![]() or diameter
or diameter ![]() …
…
![]() or
or ![]()
Coincidentally, the surface area of a sphere is ![]() times the area of the cross-sectional circle at the sphere’s widest part. You may find it interesting to try to visualize this, or head to the kitchen for a demonstration: if you cut an orange into four quarters, the peel on one of those quarter oranges has the same area as the circle formed by the first cut.
times the area of the cross-sectional circle at the sphere’s widest part. You may find it interesting to try to visualize this, or head to the kitchen for a demonstration: if you cut an orange into four quarters, the peel on one of those quarter oranges has the same area as the circle formed by the first cut.
Exercises
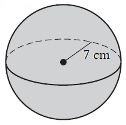
- Find the surface area of this sphere.
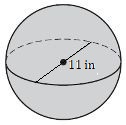
- Find the surface area of this sphere.

