13 The US Measurement System

You may use a calculator throughout this module if needed.

Robin the orange cat under a US bicentennial flag
Robin the cat has the spirit of ’76.

The U.S. customary system of measurement developed from the system used in England centuries ago.[1] To convert from one unit to another, we often have to perform messy calculations like dividing by 16 or multiplying by 5,280.

We could solve these unit conversions using proportions, but there is another method that is more versatile, especially when a conversion requires more than one step. This method goes by various names, such as dimensional analysis or the factor label method. The basic idea is to begin with the measurement you know, then multiply it by a conversion ratio that will cancel the units you don’t want and replace it with the units you do want.

It’s okay if you don’t have the conversion ratios memorized; just be sure to have them available. If you discover other conversion ratios that aren’t provided here, go ahead and write them down!

U.S. System: Measurements of Length

1 foot = 12 inches

1 yard = 3 feet

1 mile = 5,280 feet

Let’s walk through two examples to demonstrate the process.

Suppose you’re a fan of Eminem[2] or the Byrds[3] and you’re curious about how many feet are in 8 miles. We can start by writing 8\text{ mi} as a fraction over 1 and then use the conversion ratio 1\text{ mi}=5,280\text{ ft} to cancel the units.

\frac{8\text{ mi}}{1}\cdot\frac{5280\text{ ft}}{1\text{ mi}}=8\cdot5280}\text{ ft}=42,240\text{ ft}

Now suppose that you want to convert a measurement from feet to miles. (Maybe you’re watching The Twilight Zone episode “Nightmare at 20,000 Feet”[4] and wondering how many miles high that is.) We’ll start by writing 20000\text{ ft} as a fraction over 1 and then use the conversion ratio 1\text{ mi}=5,280\text{ ft} to cancel the units.

\frac{20000\text{ ft}}{1}\cdot\frac{1\text{ mi}}{5280\text{ ft}}=\frac{20000}{5280}\text{ mi}\approx3.8\text{ mi}

As it happens, the first situation became a multiplication problem but the second situation became a division problem. Rather than trying to memorize rules about when you’ll multiply versus when you’ll divide, just set up the conversion ratio so the units will cancel out and then the locations of the numbers will tell you whether you need to multiply or divide them.

Exercises

  1. How many inches are in 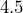4.5 feet?
  2. How many feet make up 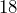18 yards?
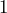  3. 1 yard is equal to how many inches?
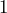  4. 1 mile is equivalent to how many yards?
  5. How many feet is 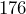176 inches?
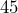  6. 45 feet is what length in yards?
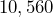  7. Convert 10,560 feet into miles.
  8. How many yards are the same as 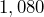1,080 inches?

Notice that Exercises 3 & 4 give us two more conversion ratios that we could add to our list.

U.S. System: Measurements of Weight or Mass

1 pound = 16 ounces

1 ton = 2,000 pounds

The procedure is the same; start with the measurement you know and write it as a fraction over 1. Then write the conversion factor so that the units you don’t want will cancel out.

Exercises

  1. How many ounces are in 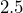2.5 pounds?
  2. How many pounds are equivalent to 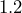1.2 tons?
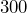  3. Convert 300 ounces to pounds.
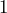  4. 1 ton is equivalent to what number of ounces?

U.S. System: Measurements of Volume or Capacity

1 cup = 8 fluid ounces

1 pint = 2 cups

1 quart = 2 pints

1 gallon = 4 quarts

There are plenty of other conversions that could be provided, such as the number of fluid ounces in a gallon, but let’s keep the list relatively short.

Exercises

  1. How many fluid ounces are in 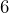6 cups?
  2. How many pints are in 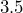3.5 quarts?
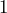  3. 1 gallon is equal to how many pints?
  4. How many cups equal 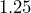1.25 quarts?
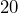  5. Convert 20 cups into gallons.
  6. How many fluid ounces are in one half gallon?

U.S. System: Using Mixed Units of Measurement

Measurements are frequently given with mixed units, such as a person’s height being given as 5 ft 7 in instead of 67 in, or a newborn baby’s weight being given as 8 lb 3 oz instead of 131 oz. This can sometimes make the calculations more complicated, but if you can convert between improper fractions and mixed numbers, you can handle this.

Exercises

  1. A bag of apples weighs 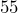55 ounces. What is its weight in pounds and ounces?
  2. A carton of orange juice contains 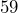59 fluid ounces. Determine its volume in cups and fluid ounces.
  3. A hallway is 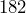182 inches long. Give its length in feet and inches.
  4. The maximum loaded weight of a Ford F-150 pickup truck is 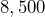8,500 lb. Convert this weight into tons and pounds.

We’ll finish up this module by adding and subtracting with mixed units. Again, it may help to think of them as mixed numbers, with a whole number part and a fractional part.

Exercises

Comet weighs 8 lb 7 oz and Fred weighs 11 lb 9 oz.

  1. Comet and Fred are being put into a cat carrier together. What is their combined weight?
  2. How much heavier is Fred than Comet?

Two tables are 5 ft 3 in long and 3 ft 10 in long.

  1. If the two tables are placed end to end, what is their combined length?
  2. What is the difference in length between the two tables?

Exercise Answers

  1. Want some Wikipedia rabbit holes? Visit https://en.wikipedia.org/wiki/United_States_customary_units and https://en.wikipedia.org/wiki/English_units. ↵
  2. https://en.wikipedia.org/wiki/8_Mile_(film) ↵
  3. https://en.wikipedia.org/wiki/Eight_Miles_High ↵
  4. https://en.wikipedia.org/wiki/Nightmare_at_20,000_Feet ↵

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Technical Mathematics, 2nd Edition Copyright © 2024 by Morgan Chase is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.