3 Decimals

Photo by Christian Collins on flickr.

Decimal notation is based on powers of 10: 0.1 is one tenth, 0.01 is one hundredth, 0.001 is one thousandth, and so on.

thousands hundreds tens ones/units . tenths hundredths thousandths

 

Exercises

Write each number.
  1. ninety and twenty-three hundredths
  2. seven and fifty-six thousandths

Adding & Subtracting Decimals

Before you add or subtract decimals, you must line up the decimal points.

Exercises

Add each pair of numbers.
  1. 3.75+12.8
  2. 71.085+112.93

When subtracting, you may need to add zeros to the first number so you can borrow correctly.

Exercises

Subtract each pair of numbers.
  1. 46.57-38.29
  2. 82.78-67.024

Multiplying Decimals

To multiply decimal numbers:

  1. Temporarily ignore the decimal points.
  2. Multiply the numbers as though they are whole numbers.
  3. Add the total number of decimal digits in the two numbers you multiplied. The result will have that number of digits to the right of the decimal point.

Note: You do NOT need to line up the decimal points when you are multiplying.

Exercises

Multiply each pair of numbers.
  1. 143\cdot29
  2. 143\cdot2.9
  3. 14.3\cdot2.9
  4. 1.43\cdot2.9
  5. 375\cdot175
  6. 375\cdot0.175
  7. 3.75\cdot1.75
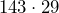
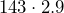
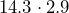
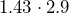
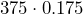
  8. Evie worked 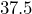37.5 hours at a pay rate of 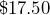\textdollar17.50 per hour. How much did she earn in total?

Dividing Decimals

Let’s review everyone’s favorite topic, long division. The three parts of a division are named as follows: dividend \div divisor = quotient. When this is written with a long division symbol, the dividend is inside the symbol, the divisor is on the left, and the quotient is the answer we create on top.

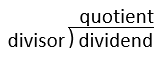
long division symbol with "dividend" inside the symbol, "divisor" on the left, and "quotient" on top

To divide by a decimal:

  1. Write in long division form.
  2. Move the decimal point of the divisor until it is a whole number.
  3. Move the decimal point of the dividend the same number of places to the right.
  4. Place the decimal point in the quotient directly above the decimal point in the dividend.
  5. Divide the numbers as though they are whole numbers.
  6. If necessary, add zeros to the right of the last digit of the dividend to continue.

Exercises

Divide each pair of numbers.
  1. 974\div4
  2. 974\div0.4
  3. 9,740\div0.04
  4. 0.0974\div0.004

Rounding Numbers

It is often necessary to round a number to a specified place value. We will see more specific instructions in Modules 5 & 6, but let’s review the basics of rounding a number.

Rounding a number:

  1. Locate the rounding digit in the place to which you are rounding.
  2. Look at the test digit directly to the right of the rounding digit.
  3. If the test digit is 5 or greater, increase the rounding digit by 1 and drop all digits to its right.
  4. If the test digit is less than 5, keep the rounding digit the same and drop all digits to its right.

Exercises

Round each number to the indicated place value.
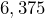  1. 6,375 (thousands)
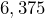  2. 6,375 (tens)
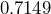  3. 0.7149 (hundredths)
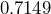  4. 0.7149 (thousandths)

If a decimal answer goes on and on, it may be practical to round it off.

Exercises

  1. A subscription to The Chicago Manual of Style Online costs 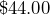\textdollar44.00. Determine the monthly cost, rounded to the nearest cent.
  2. In the summer of 1919, a military convoy (including Lt. Col. Dwight Eisenhower) drove from Washington, D.C. to San Francisco to assess the condition of the nation’s developing highway system. The journal entry for August 1 says “Good dirt roads. Made 82 miles in 11 hrs.”[1] What was the convoy’s effective speed in miles per hour for that day? Round your result to the nearest tenth.

Exercise Answers

  1. Source: https://after-ike.com/logbook-1919-transcontinental-military-convoy/. See https://www.nytimes.com/2019/07/07/opinion/the-most-important-road-trip-in-american-history.html if you're interested in the historical context. ↵

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Technical Mathematics, 2nd Edition Copyright © 2024 by Morgan Chase is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.