Converting Units of Area

Morgan Chase

21 Converting Units of Area

You may use a calculator throughout this module.

When we are converting between units of area, we need to be aware that square units behave differently than linear units. We’ll begin by using our knowledge of linear units to investigate how area conversions are different.

U.S. System: Converting Measurements of Area

Exercises

A hallway’s floor is 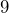$9$ yards long and 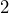$2$ yards wide. Convert each measurement to feet, then determine the area of the floor in square feet.
A hallway’s floor has an area of 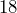$18$ square yards. Determine the area of the floor in square feet.
A tabletop measures 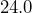$24.0$ inches by 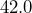$42.0$ inches. Convert each measurement to feet, then determine the area of the tabletop in square feet.
A tabletop has an area of 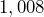$1,008$ square inches. Determine the area of the tabletop in square feet.

It may help to visualize the relationship between square yards and square feet. Consider a square yard; the area of a square with sides $1$ yard long.
a square that has sides 1 yard long

We know that $1$ yard = $3$ feet, so we can divide the square into three sections vertically and three sections horizontally to convert both dimensions of the square from yards to feet.

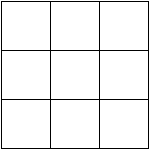
a 3 by 3 grid representing 9 square feet

This forms a $3$ by $3$ grid, which shows us visually that $1$ square yard equals $9$ square feet! Instead of $1$ to $3$ , the conversion ratio for the areas is $1$ to $3^2$ , or $1$ to $9$ .

Here’s another way to think about it without a diagram: $1\text{ yd}=3\text{ ft}$ , so $(1\text{ yd})^2=(3\text{ ft})^2$ . To remove the parentheses, we must square the number and square the units: $(3\text{ ft})^2= 3^2\text{ ft}^2=9\text{ ft}^2$ .

More generally, we need to square the linear conversion factors when converting units of area. If the linear units have a ratio of $1$ to $n$ , the square units will have a ratio of $1$ to $n^2$ .

Here are the conversion ratios for area in the U.S. system. As always, if you discover other conversion ratios that aren’t provided here, it would be a good idea to write them down so you can use them as needed.

$1\text{ ft}^2=144\text{ in}^2$

$1\text{ yd}^2=9\text{ ft}^2$

$1\text{ yd}^2=1,296\text{ in}^2$

$1\text{ acre (ac)}=4,840\text{ yd}^2$

$1\text{ ac}=43,560\text{ ft}^2$

$1\text{ mi}^2=640\text{ ac}$

$1\text{ mi}^2=3,097,600\text{ yd}^2$

$1\text{ mi}^2=27,878,400\text{ ft}^2$

If you’re curious, an acre is defined as the area of a $660$ foot by $66$ foot rectangle. (That’s a furlong by a chain. Why? Because that’s the amount of land that a medieval farmer with a team of eight oxen could plow in one day.)^[1] An acre is defined as a unit of area; it would be wrong to say “acres squared” or put an exponent of $2$ on the units.

Exercises

A rectangular sheet of fabric has an area of 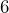$6$ square yards. Find its area in square inches.
A proposed site for an elementary school is 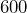$600$ feet by 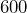$600$ feet. Determine its area in acres, rounded to the nearest tenth.

Metric System: Converting Measurements of Area

Now let’s take a look at converting area using the metric system.

Exercises

A hallway’s floor is 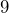$9$ meters long and 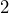$2$ meters wide. Convert each measurement to centimeters, then determine the area of the floor in square centimeters.
A hallway’s floor has an area of 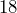$18$ square meters. Determine the area of the floor in square centimeters.
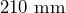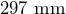A sheet of A4 paper measures $210\text{ mm}$ by $297\text{ mm}$ . Convert each measurement to centimeters, then determine the area in square centimeters.
A sheet of A4 paper has an area of 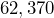$62,370$ square millimeters. Determine the area in square centimeters.

As shown below, the conversions in the metric system are all powers of ten, which means they are all about moving the decimal point.

$1\text{ cm}^2=100\text{ mm}^2$

$1\text{ m}^2=10,000\text{ cm}^2$

$1\text{ m}^2=1,000,000\text{ mm}^2$

$1\text{ hectare (ha)}=10,000\text{ m}^2$

$1\text{ km}^2=1,000,000\text{ m}^2$

$1\text{ km}^2=100\text{ ha}$

A hectare is defined as a square with sides $100$ meters long. Dividing a square kilometer into ten rows and ten columns will make a $10$ by $10$ grid of $100$ hectares. As with acres, it would be wrong to say “hectares squared” or put an exponent of $2$ on the units.

Exercises

A rectangular sheet of fabric has an area of 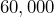$60,000$ square centimeters. Find its area in square meters.
A proposed site for an elementary school is 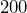$200$ meters by 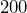$200$ meters. Find its area, in hectares.

Both Systems: Converting Measurements of Area

Converting between the U.S. and metric systems will involve messy decimal values. For example, because $1\text{ in}=2.54\text{ cm}$ , we can square both numbers and find that $(1\text{ in})^2=(2.54\text{ cm})^2=6.4516\text{ cm}^2$ . The conversions are rounded to five significant figures in the table below.

$1\text{ in}^2=6.4516\text{ cm}^2$

$1\text{ m}^2\approx10.764\text{ ft}^2$

$1\text{ m}^2\approx1.1960\text{ yd}^2$

$1\text{ mi}^2\approx2.5900\text{ km}^2$

$1\text{ ha}\approx2.4711\text{ ac}$ or $1\text{ ac}\approx0.40469\text{ ha}$

Exercises

The area of Portland, Oregon is 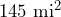$145\text{ mi}^2$ . Convert this area to square kilometers.
How many hectares is a 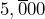$5,\overline{0}00$ acre ranch?
A standard sheet of paper measures 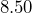$8.50$ inches by 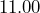$11.00$ inches. What is the area in square centimeters?
A football pitch (soccer field) is 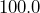$100.0$ meters long and 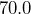$70.0$ meters wide. What is its area in square feet?

Before the Denmark v Germany match, Rotterdam, Women’s Euro 2017.

Areas of Similar Figures

Earlier in this module, it was stated that if the linear units have a ratio of $1$ to $n$ , the square units will have a ratio of $1$ to $n^2$ . This applies to similar figures as well.

If the linear dimensions of two similar figures have a ratio of $1$ to $n$ , then the areas will have a ratio of $1$ to $n^2$ .

This is true for circles, similar triangles, similar rectangles, similar hexagons, you name it. We’ll verify this in the following exercises.

Exercises

A personal pizza has a $7$ -inch diameter. A medium pizza has a diameter twice that of a personal pizza.

Determine the area of the medium pizza.
Determine the area of the personal pizza.
What is the ratio of the areas of the two pizzas?

A right triangle has legs $3\text{ cm}$ and $4\text{ cm}$ long. A larger right triangle has legs triple these dimensions.

Determine the area of the larger triangle.
Determine the area of the smaller triangle.
What is the ratio of the areas of the two triangles?

Exercise Answers

Source: https://en.wikipedia.org/wiki/Acre ↵

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License