Springs

The predictable and repeatable way in which springs stretch in response to applied forces provides a method for measuring weight and other forces. Furthermore, springs can be designed to produce conveniently measurable stretch distances for a wide variety of forces.  For example, if you were pull on each end of a steel wire that had the same diameter as a human hair,  you would not be able to noticeably stretch the wire. However, if that wire were formed into a spring, then you could stretch the spring with your bare hands.

^[1]

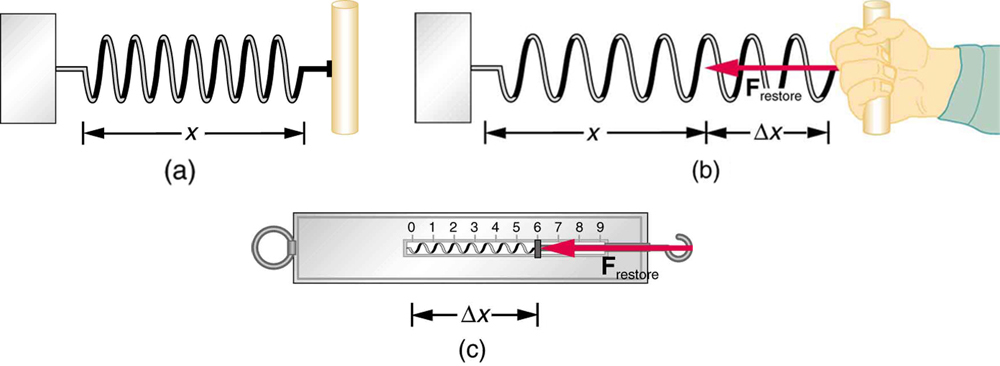
Springs follow Hooke's Law which states that the restoring force, F_R exerted by the spring is equal to the stretch or compression distance, known as the displacement (Δx), multiplied by spring stiffness (k) and the direction of the force is opposite to the direction of the displacement.

(1)  

A higher spring stiffness means the spring shows a greater resistance to stretching or compressing. Spring stiffness is often called the spring constant. The negative sign tells us that the restoring force provided by the spring always points in the opposite direction as the displacement.

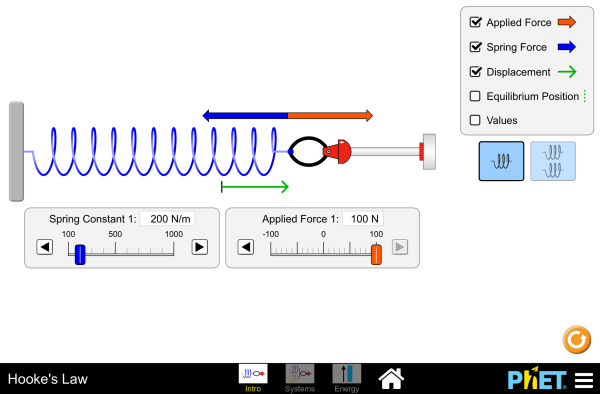
Check out this simulation of Hooke's Law:

Vectors

As we analyze forces we are beginning to see that it’s very important to keep track of their directions in order to know if they are cancelling out or adding together, which is why we represent them with vectors. As we move through the textbook we will encounter a few other quantities that are also vectors and we will need to remember which quantities require keeping track of their direction (vectors) and which don’t (scalars). For example, the displacement of the spring is vector because is has a size that tells us how far it was displaced, and a direction that tells whether it was stretched or compressed that distance. We will make the symbols for vectors bold when writing equations. We should be able to avoid confusion with our bold units by only writing units behind numeric values and not behind symbols. You may have noticed that already started using this bold convention in the equation for the spring above. In some cases we might only be interested the size of a vector, called the magnitude, and then we will not make it bold.

Weight with a Spring Scale

Spring scales are designed to take advantage of Hooke's law to determine the size of the force stretching the spring by measuring the displacement. For example when hanging the object from the spring scale the force of gravity will pull it down and the restoring force in the spring pulls it up, as represented by the free body diagram of the turtle  in the following image:

^[2]

When weighing an object that is not accelerating we know that the restoring force from the scale must perfectly balance the weight. Therefore, if we are careful to make sure the object remains still we can measure the weight by finding the restoring force from the spring, which is determined by the displacement. Typically spring scales will have markings on them which indicate the restoring force for each stretch distance so we can read off the spring force and immediately know the weight, if the object is not accelerating.

You might be wondering how we can know that the spring force and the weight are balanced just because the object is not accelerating (a.k.a. not changing velocity).  This is actually a conclusion based on Newton's First Law of Motion, which tells us that an object will not change velocity unless it experiences an unbalanced force, (but if it does experience an unbalanced force then it will change it’s velocity). When an object is not moving then it’s velocity is zero and not changing so it must have balanced forces and we say that such objects are in static equilibrium.  If the object is moving, but its velocity is constant the we say the object is in dynamic equilibrium. In either case, equilibrium refers to the fact that the forces are balanced. Notice that we could still get a correct reading from the spring scale if we moved it at constant velocity, but that is very hard to do. Instead, we hold the objects still to keep the velocity constant (at zero) and ensure that the forces are balanced so that the scale reading is equal to the weight.

Many analog scales are based on multiple springs or the resistance to deformation by objects other than springs, but they still determine the weight of an object in equilibrium by using measurement of deformation in the scale and a known relation between deformation and force.

Digital Scales

Many modern scales follow the same principle as spring scales, but instead of measuring the deformation directly, they measure an electric voltage created by a material in response to being deformed. Materials that produce voltages in response to deformation are known as  piezoelectrics. As long as the relations between voltage and deformation and between deformation and applied force are both known, the scale can determine your weight by measuring a voltage.

An interesting aspect of the piezoelectric effect is reversibility, meaning that piezoelectric materials not only produce a voltage in response to deformation, they will also deform in response to an applied voltage,  which allows for piezoelectric motors.