Impact Forces

Lawrence Davis

58 Impact Forces

Impulse

In the previous sections analyzed systems that were isolated so we knew that the total momentum of the system could not change. Now we would like to analyze systems that are not isolated, meaning they do feel a net external force. For example, the individual components of the larger systems are just smaller systems themselves, and those smaller systems certainly did experience changes in velocity.

Animated GIF — Sitting in a wheeled chairs, Science Lab Technician Becky Kipperman (left) and Chemistry Professor Sean Breslin (right) push against one another while the author is attached to Sean in another chair, but not touching the floor. This collision causes a leftward change in motion for Becky and a much smaller rightward change in motion for Sean and the author. Overall, the center of mass velocity of the whole system does not change.

When the net external force on a system is not zero, then the system momentum will change according to the Impulse-Momentum Theorem:

(1) $\begin{equation*} \Delta t \bold{F_{ave}} = m\bold{v_f}-m\bold{v_i} \end{equation*}$

The left side of the equation, average force multiplied by the collision time, is known as the impulse (I). The right side of the equation is the initial momentum subtracted from final momentum, also known as the change in momentum. Notice that we have assumed the mass of the system did not change so we did not designate initial and final mass. In that case we could simplify the change-in-momentum side by factoring out the mass and using standard notation for a change

(2) $\begin{equation*} \Delta t \bold{F_{ave}} = m\bold{\Delta v} \end{equation*}$

Either way, we see that changes in momentum require some non-zero net external force to be applied for some non-zero amount of time, which agrees with Newton’s First Law, but now for the first time we can actually analyze the forces on systems that are not in equilibrium.

Fall Speed from Impulse

In the very first unit we used the kinematic equations to find the speed an object reaches after falling for a certain time. Now let’s use the Impulse-Momentum Theorem to calculate the fall speed and check that we get the same result.

Everyday Example: Fall Speed

Neglecting air resistance, what velocity will a person have after falling for 0.5 s when they started at rest?

Starting with the impulse-momentum theorem for an object with constant mass:

(3) $\begin{equation*} \Delta t \bold{F_{ave}} = m \bold{\Delta v} \end{equation*}$

This equation requires that we keep track of direction (it is a vector equation). Let’s choose down as the positive direction so the force of gravity will be positive. Gravity is the only force on the person, so the average net force is $F_{ave} = mg$ . We can also expand the change in velocity to express show the final and initial values:

(4) $\begin{equation*} \Delta t mg = m(\bold{v_f} -\bold{v_i}) \end{equation*}$

We can cancel the masses (by dividing both sides by mass) and the initial velocity was zero because they started at rest:

(5) $\begin{equation*} \Delta t g = \bold{v_f} -0 \end{equation*}$

Notice that this result exactly what we would find if we used the free-fall acceleration in the kinematic equations from the first unit. Entering the values for g and the fall time:

(6) $\begin{equation*} (0.5\,\bold{s})(9.8 \,\bold{m/s/s}) = \bold{v_f} =4.9 \,\bold{m/s} \end{equation*}$

Reinforcement Activity

Reinforcement Exercises

NEt impulse

In cases when multiple forces act on an object during a collision, we need to be sure to calculate the net impulse by calculating the individual impulses from each force and then adding them up. Alternatively we can calculate the the net force first and then use that in the impulse calculation to get net impulse directly.

Everyday Examples: Landing after a Jump

You naturally tend to bend your knees when landing after a jump, rather than keep your knees locked and your legs rigid. The reason is that rigid legs bring you to an abrupt stop, but bending your knees allows you to spread the landing out over a longer time which reduces the average and peak force applied to your legs.

A person steps off a small platform onto a force plate and on one foot with a stiff leg. The same person then steps off again and bends their leg as they land. — Stiff and bent-leg landings that produced the force vs. time data shown below.

The force vs. time graphs allow us to visualize the normal force applied to the person landing on one foot after stepping off from a 0.1 m height as seen in the previous GIF. The graph on the left was the more rigid leg landing (it didn’t feel good) and the graph on the right was a bent-knee landing.

Force vs. time curves: Stiff-leg hard-landing curve starts at zero then spikes to 2000 N for roughly 0.2 s before returning to a constant value near 800 N (bodyweight). Bent-leg, soft-landing starts at zero, jumps to 1000 N, creating a rounded bump roughly 0.4 s wide before returning to roughly 800 N and remaining constant. — Force vs. time data for a stiff-legged landing (red) and crouching landing (blue).

In both cases the force eventually stabilizes at a value equal to the body weight because the body ends up in static equilibrium. In the stiff-legged landing we see that the platform applies a force much larger than body weight for a very short time. In the graph on the right we see that the force was much lower, but was larger than body weight for a longer period of time. We can understand this in terms of the Impulse-Momentum Theorem. The impulse causing the change in momentum can be provided by a large force applied over a short time or a small force applied for a longer time.

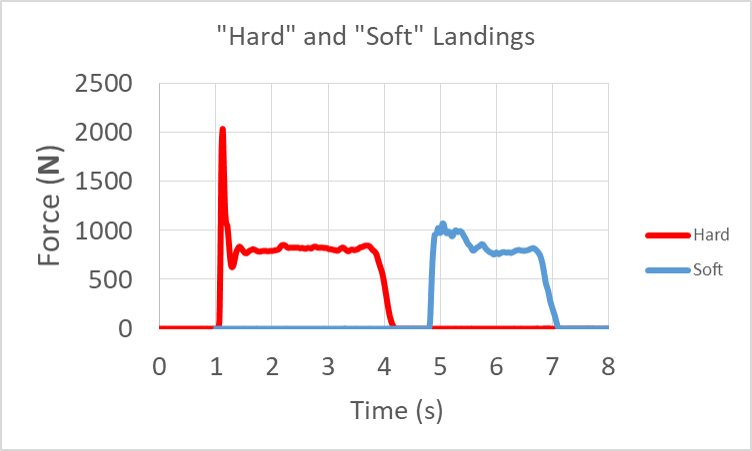
In the previous example we compared the impact forces generated by “hard” and “soft” landings. However, that comparison assumed that the subject in the video had to the same impact velocity in each trial simply because they stepped from the same height. The author might have been sneaky and purposefully changed the impact velocity between the trials by holding the back foot on the platform for longer . We can actually use the Impulse-Momentum Theorem to verify the subject had a similar impact velocity in both trials.

Examples: Impact Velocity

The force vs. time graphs in the previous example allows us to visualize the normal force applied to the person landing on one foot after stepping off from a 0.1 m height. We wan to verify that the person had the same impact velocity in both trials. If both trials had the same impact velocity then the change in momentum was also the same (both ended with zero velocity and the mass did not change between trials). Therefore we can verify the similarity in impact velocities by verifying that the impulse received by the person was the same in both trials. the . Let’s walk through that reasoning step by step, starting with the impulse-momentum theorem:

(7) $\begin{equation*} \Delta t \bold{F_{ave}} = m \bold{\Delta v} \end{equation*}$

We can expand the change in velocity:

(8) $\begin{equation*} \Delta t \bold{F_{ave}} = m (\bold{v_f}-\bold{v_i}) \end{equation*}$

Both trials ended with zero velocity:

(9) $\begin{equation*} \Delta t \bold{F_{ave}} = m(- \bold{v_i}) \end{equation*}$

The negative sign indicates that the net force points in the opposite direction to the impact velocity, as expected because the object slows down on landing. The mass did not change between trials so if we verify that both impacts produced the same impulse then the impact velocity must have been the same for both trials. Let’s start with the hard landing.

The force reading jumps up nearly vertically to 2000 N and then stabilizes to the persons body weight of 750 N over about 0.2 s. We can estimate the upward normal force on the person during the interval as the average of 2000 N and 750 N which is 1375 N. The person’s body weight is acting down while this normal force act upward, so the average net force is actually $1375\bold{N} -750\bold{N} =625\bold{N}$ . The net impulse is then:

(10) $\begin{equation*} \Delta t \bold{F_{ave}} = (0.2\,\bold{s})(625\,\bold{N}) = 125\,\bold{Ns} \end{equation*}$

Now for the soft landing we see a similar initial sharp jump up to 1000 N and then a gradual decrease to 750 N over roughly a whole second (just before 5 s to just before 6 s). The average upward force is 875 N. To get net force we subtract the body weight, $875\bold{N} -750\bold{N} =125\bold{N}$ . Then net impulse is then:

(11) $\begin{equation*} \Delta t \bold{F_{ave}} = (1\,\bold{s})(125\,\bold{N}) = 125\,\bold{Ns} \end{equation*}$

According to our estimates both landings produced the same net impulse of roughly 125 Ns. Therefore, the impact velocities must have been approximately the same yet we saw that the hard landing produced twice the peak force, which is why landing with straight legs is not a good idea.

We can actually use the impulse to calculate the impact velocity for this case if we know the mass. Starting with our equation for impulse in this case of zero final velocity:

(12) $\begin{equation*} \Delta t \bold{F_{ave}} = m(- \bold{v_i}) \end{equation*}$

Divide by mass and by -1 to isolate the impact velocity:

(13) $\begin{equation*} -\frac{\Delta t \bold{F_{ave}}}{m} = \bold{v_i} \end{equation*}$

We know the impulse is 125 Ns, but we still need the mass. We can get the mass by dividing the 750 N body weight by g to get $(750\,\bold{N})/(9.8\,\bold{m/s/s}) = 76.5\,\bold{kg}$ . Entering the impulse and mass values:

(14) $\begin{equation*} -\frac{125\,\bold{Ns}}{76.5\,\bold{kg}} = 1.6\,\bold{m/s} = \bold{v_i} \end{equation*}$

*If you use the kinematic equations to calculate the expected speed for a drop height of 0.1 m you will get 1.4 m/s, which is 13% different from what we found above and very reasonable considering that we estimated our impulse by reading values off the graph.*