Collision Energy

All of the example collisions we have analyzed so far have been inelastic collisions because the kinetic energy of the system changed during the collision between components of the system.  It is very important to recognize that both the momentum and total energy  of an isolated system are still conserved during an inelastic collision, even though the kinetic energy changes to another form.   When objects start connected and separate or start separated and then collide and stick together we say the collision is perfectly inelastic collisions. Those types of collisions are easier to analyze because we know that the two objects either had the same initial velocity or the same final velocity and so we have fewer variables to deal with. Those types of collisions also maximize the dissipation of kinetic energy to thermal energy.

Crumple Zones

Crumple zones built into modern cars also serve the purpose of reducing force by increasing the collision compression distance (and also time) and by minimizing bounce (change in velocity). Crumple zones cause cars to be totaled more often, but replacing cars is possible and replacing people is not.

Notice that the presenter in the previous video mentions absorbing energy. This energy that he is claiming will be absorbed by the crumple zone is the kinetic energy stored in the motion of the car. If you watch the video carefully, you see that the car was moving forward, then for a moment it was stopped and thus had zero kinetic energy, and then it was moving backward (though not as fast), so once again it had kinetic energy.  Some of the original kinetic energy was stored as elastic potential energy within the compressed material, and then released as kinetic energy again as the car bounced, but most was transferred to thermal energy.

The force applied to the materials during the collision caused a stress on the materials. Some materials were stressed above their ultimate strength so they fractured. Some other materials didn’t fracture, but were stressed into their failure region so that they were permanently deformed. In either case, the work done to deform the materials transferred kinetic energy into thermal energy, effectively slowing the car down, but warming it up.

If the car had bounced back at the same speed that it had entering the collision, then the final kinetic energy would be the same as the initial and we would say that kinetic energy had been conserved. Collisions that conserve kinetic energy are known as elastic collisions. The purpose of crumple zones is to minimize bounce by dissipating kinetic energy to thermal energy and to reduce collision force by extending the distance over which that dissipation work is done.

Bounce is Bad

Cars could use springy materials to extend the collision time and distance without causing so much damage to the cars, but that would cause the collisions to be bouncy.  Older model cars were often designed with very strong rigid frames in order to “protect” occupants during a crash. However, the materials were so strong that they did not deform much during accidents. The small deformation caused the collision to happen over a short distance, which increased the average force applied to the occupants. Worse yet, the rigid frames bounce more than crumple zones, which further increases the force on occupants. Even if we designed an elastic car that was able to deform by the same amount as the crumple zone, that elastic car would still apply a higher peak force to the occupants (though the average force would be the same), as we can see from the following example.

Everyday Examples: Collision with Stationary Barrier

Let’s compare the max force applied during perfectly inelastic and elastic collisions between a car and a solid wall that doesn’t move. We will assume the elastic car is designed to deform over the same distance as the inelastic car and apply energy conservation to first half of the collision. Our system will include the car and the barrier.

Elastic and Inelastic Collision Force Comparison

Constant Dissipative Force (Converts KE to TE)	Spring Force (Converts KE to PE and back to KE)
Internal work is done to convert KE to TE. Assume that work is done by a constant force over the total crumple distance, . No energy is stored as PE	Internal work is done to convert KE to PE over the total compression distance, . No energy is converted to TE.
Expand the changes	Expand the changes
Final kinetic energy is zero.	Initial potential energy and final kinetic energy are zero. Split the into
Isolate the force in the previous equation	The force to compress a spring is Make that substitution.
For a constant force, that is the average and the max.	Cancel the 1/2 in each term and isolate the max force. The spring force is proportional to compression distance, so the average force will be half of the max.
	and  \frac{mv_i^2}{2x}$

We see that the average force is the same in both cases, but the peak force is larger for the elastic collision.

Not only do bouncy collisions increase the overall impact force on a system, they also lead to greater impact speeds, and therefore forces, between individual components of the system. For example, if the car bounces then the occupant’s head may still be moving forward while the dashboard is moving backward, which effectively doubles the impact speed between head and dashboard. The same thing can then happen again with your brain inside your skull. Airbags are designed to prevent that.

Everyday Example: Air Bags

If the skull impacts a hard surface, but neither the skull or surface are significantly deformed, then the skull will bounce back. The skull did not stick to the surface so this collision is not perfectly inelastic like those we have analyze up to this point. As the skull bounces back the brain continues to move forward due to inertia and the relative impact speed brain and skull is nearly twice what it would have been if the skull had simply stopped (as it would for a perfectly inelastic collision).

^[1]

After the bounce, as the neck causes the skull to slow down on the way backward, the inertia of the brain may lead to a second impact on the back of the brain, as illustrated in the previous image. Aside from an additional brain tissue injury, the combined swelling of the two opposed injuries will put amplify the pressure on the brain and increase the likelihood of permanent injury. This type of injury is known as a Coup Countrecoup , or translated from French by Google Translate, blow, counter blow.

Check out this video of crash-testing with and without airbags.

During the crash the driver’s head starts out with the same velocity  as the car. The airbag increases the time it takes for the head to come to rest, which will decrease the force on the head. In order make sure the head does actually come to rest instead of bouncing the airbag has vents that allow air to be pushed out during impact so  it deflates instead of staying completely full and acting like a bouncy beach ball.

Coefficient of Restitution

The relative elasticity of collisions is defined by the coefficient of restitution (COR). For a moving object striking a stationary object that doesn’t move, as in the crumple zone video, the COR is calculated as final speed divided by initial speed.

(1)  

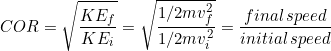
A perfectly elastic collision would have a COR of one.  If any materials are permanently deformed during a collision then you can be sure the collision was not perfectly elastic. In fact, perfectly elastic collisions don’t really occur on a macroscopic scale, but many situations come very close and we can approximate them as perfectly elastic. On the microscopic scale, collisions between atoms and elementary particle can appear perfectly elastic because thermal and kinetic energy are the same thing on a microscopic scale. However, atoms can emit light waves that carries away energy to create inelastic collisions.

Check out this simulation that allows you to visualize different types of collisions.