Tipping

Lawrence Davis

40 Tipping

Torque

When you hold an object in your hand, the weight of the object tends to cause a rotation of the forearm with the elbow joint acting as the pivot. The tension force applied by your biceps tries to counteract this rotation.

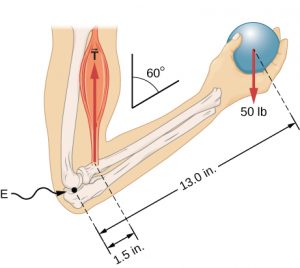
Figure is a schematic drawing of a forearm rotated around the elbow. A 50 pound ball is held in the palm. The distance between the elbow and the ball is 13 inches. The distance between the elbow and the biceps muscle, which causes a torque around the elbow, is 1.5 inches. Forearm forms a 60 degree angle with the upper arm. — The elbow joint flexed to form a 60° angle between the upper arm and forearm while the hand holds a 50 lb ball. The weight of the ball exerts a torque on the forearm *about* the elbow joint. Image Credit: Openstax University Physics

^[1]

When forces applied to an object tend to cause rotation of the object, we say the force is causing a torque. The size of a torque depends on the size of the force, the direction of the force, and the distance from the pivot point to where the force acts.

Reinforcement Activity

Static Equilibrium

We already know that when an object must have no net force in order for its velocity to remain constant, meaning that it’s translational motion did not change. In similar fashion, on object with constant rotational motion must have zero net torque. Therefore, in order for an object to remain still without rotating all the torques must cancel each other out. If the net torque is not zero the the object will begin to rotate rather than remain still. For example, in our example of the forearm holding the ball, the torque due to biceps tension and torque due to ball weight must be equal, but in opposite directions.

Reinforcement Exercises

Tipping Point

When a body’s center of gravity is above the area formed by the support base the normal force can provide the torque necessary to remain in rotational equilibrium.

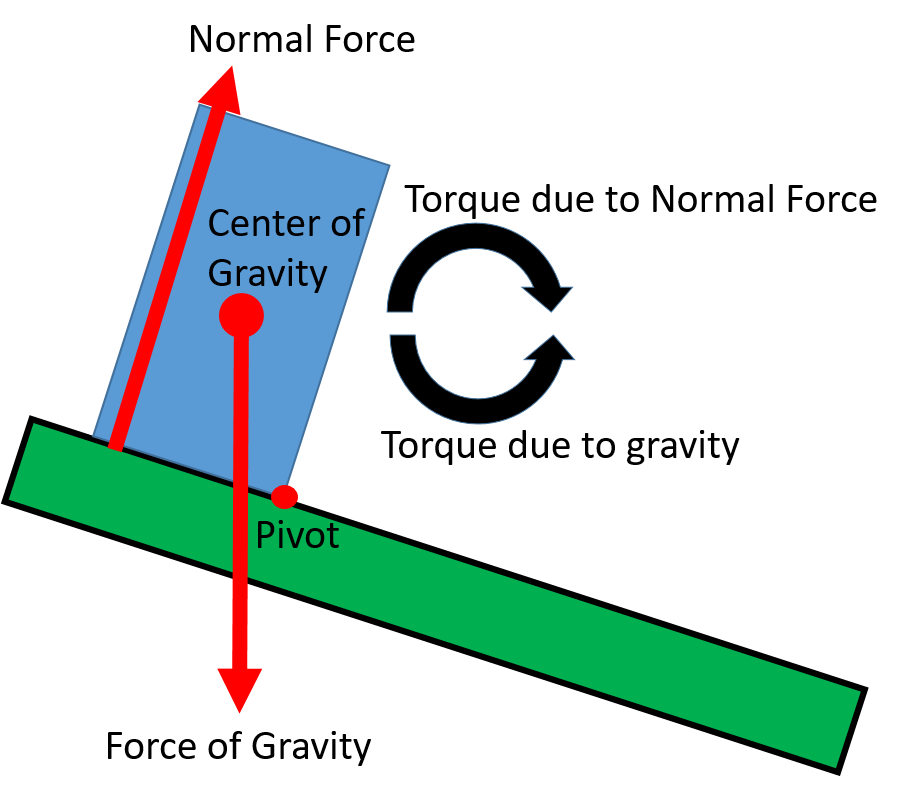
A box sits with its bottom flush against sloping ground. An arrow labeled normal force points upward from bottom of the box on the uphill side. An arrow labeled force of gravity points downward from the center of the box. The downhill bottom corner of the box is labeled as pivot. A rightward curved arrow is labeled torque due to normal force. An equal size, but oppositely curved arrow is labeled torque due to gravity. — An object in rotational equilibrium. The torque from normal force cancels the torque from gravity. In this case friction (not shown) acts on the bottom surface of the object to keep it from sliding downhill.

The critical tipping point is reached when the center of gravity passes outside of the support base. Beyond the tipping point, gravity causes rotation away from the support base, so there is no normal force available to cause the torque needed to cancel out the torque caused by gravity. The normal force acting on the pivot point can help support the object’s weight, but it can’t create a torque because it’s not applied at any distance away from the pivot.

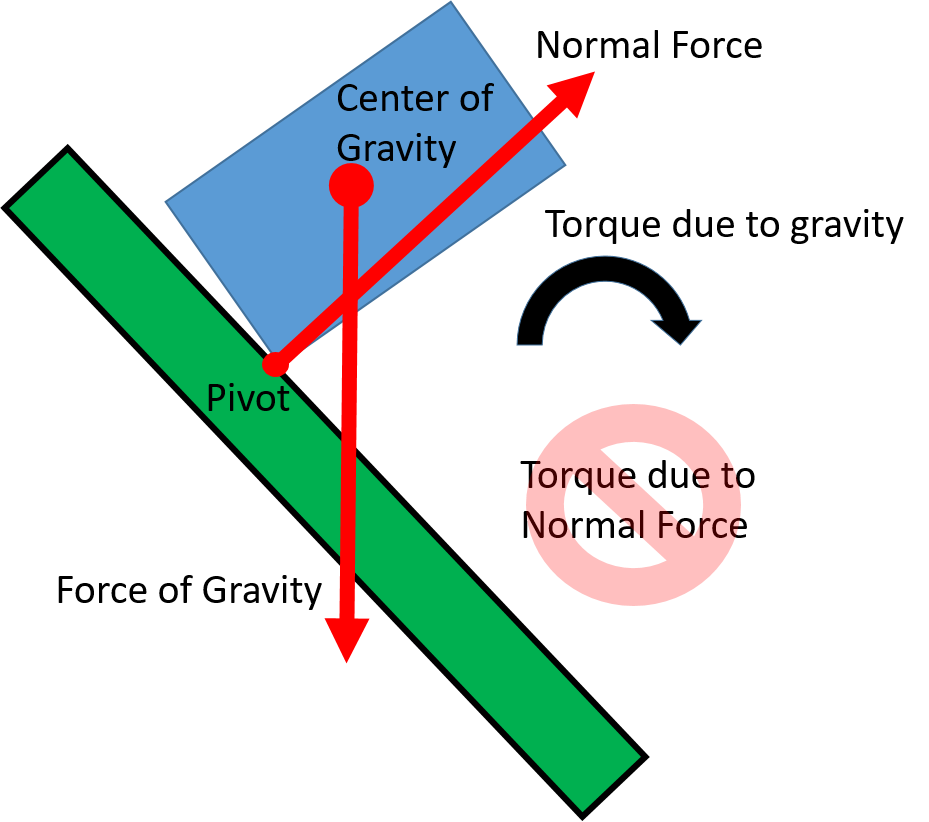
A box is in the process of tipping over on sloping ground. An arrow labeled force of gravity points downward from the center of the box. The downhill bottom corner of the box is labeled as pivot. An arrow labeled normal force points upward from the pivot. A rightward curved arrow is labeled torque due to gravity. Torque due to normal force is slashed through to indicate its absence. — An object out of rotational equilibrium. The normal force acting at the pivot cannot produce a torque to cancel the torque caused by gravity. In this case friction (not shown) acts at the pivot point to keep the object from sliding downhill.

Now with a net torque the object can not be in rotational equilibrium. The object will rotate around the edge of the support base and tip over. We often refer to structures (and bodies) that are relatively resistant to tipping over as having greater stability.

OpenStax University Physics, University Physics Volume 1. OpenStax CNX. Jul 11, 2018 http://cnx.org/contents/d50f6e32-0fda-46ef-a362-9bd36ca7c97d@10.18. ↵

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License