89 Cold Weather Survival Time
| Stage | Core Body Temperature °C | Symptoms |
| Mild Hypothermia | 35°-33° | shivering, poor judgment, amnesia and apathy, increased heart and respiratory rate, cold and/or pale skin |
| Moderate Hypothermia | 32.9°-27° | progressively decreasing levels of consciousness, stupor, shivering stops, decreased heart and respiratory rate, decreased reflex and voluntary motion, paradoxical undressing. |
| Severe Hypothermia | < 26.9° | low blood pressure and bradycardia, no reflex, loss of consciousness, coma, death |
Throughout this unit we have analyzed the rate of heat loss during a cold weather survival situation in which a person is wearing a single layer of thin clothing against an 10 mph wind and a -3 °C air temperature. Our analysis shows that collectively the person would experience a 200 W heat loss rate due to thermal radiation and a 1100 W heat loss rate due to forced convection. We also found that using a space blanket to reduce the wind chill and thermal radiation would leave only 160 W of heat loss rate due to conduction across the clothing. The typical person has a thermal power of 100 W, but shivering can increase that to 250 W.[2] It would be interesting to know, given these values for thermal power and heat loss rate, how quickly body temperature would actually change. In order to answer that question we need to learn about specific heat and heat capacity.
Human Heat Capacity
In the fight to maintain body temperature the human body gets assistance from the fact that the body is primarily made of water. The amount of thermal energy required to change the temperature of the body is relatively high compared to other objects of the same mass because water has a very high specific heat (c). Specific heat is a material property that defines the amount of thermal energy removed from one unit mass of the material when it’s temperature changes by one unit of temperature. For example, water has a specific heat of 4186 J/(kg C°) so 4186 J of thermal energy must be removed from 1 kg of water in order for the temperature to drop by 1 C°. Multiplying the specific heat of a material by the mass of the material gives the heat capacity (C) of the object. For example, the heat capacity for 80 kg of water would be: 4186 J/(kg C°) x 80 kg = 334,880 J/(C°), meaning that 334,880 J must be removed to drop the temperature of 80 kg of water by 1 C°.
Reinforcement Exercises
Now that we know how to calculate heat capacity we are ready to calculate the amount of energy required to change the temperature of the body by a dangerous amount. We just multiply the mass (m) by the specific heat (c) to get heat capacity, which we then we multiply by a dangerous temperature change (
) to get the heat required (Q). This entire process can be summed up by the equation:
(1) 
Notice that if the temperature is dropping then final temperature is less than the initial temperature so 
will be negative, which makes heat negative, indicating that thermal energy is leaving the object. The equation works for heating as well as cooling because in that case and 
will be positive indicating that thermal energy is entering the material.
Reinforcement Exercises
The following chart provides specific heat values for various substances. Notice the relatively high specific heat of water.
| Substances | Specific heat (c) | |
| Solids | J/kg⋅ºC | kcal/kg⋅ºC |
| Aluminum | 900 | 0.215 |
| Asbestos | 800 | 0.19 |
| Concrete, granite (average) | 840 | 0.20 |
| Copper | 387 | 0.0924 |
| Glass | 840 | 0.20 |
| Gold | 129 | 0.0308 |
| Human body (average at 37 °C) | 3500 | 0.83 |
| Ice (average, -50°C to 0°C) | 2090 | 0.50 |
| Iron, steel | 452 | 0.108 |
| Lead | 128 | 0.0305 |
| Silver | 235 | 0.0562 |
| Wood | 1700 | 0.4 |
| Liquids | ||
| Benzene | 1740 | 0.415 |
| Ethanol | 2450 | 0.586 |
| Glycerin | 2410 | 0.576 |
| Mercury | 139 | 0.0333 |
| Water (15.0 °C) | 4186 | 1.000 |
| Gases | ||
| Air (dry) | 721 (1015) | 0.172 (0.242) |
| Ammonia | 1670 (2190) | 0.399 (0.523) |
| Carbon dioxide | 638 (833) | 0.152 (0.199) |
| Nitrogen | 739 (1040) | 0.177 (0.248) |
| Oxygen | 651 (913) | 0.156 (0.218) |
| Steam (100°C) | 1520 (2020) | 0.363 (0.482) |
Everyday Examples: Cold Weather Survival Time
Applying the previous equation to the human body we can estimate how long it would take body temperature to drop from a normal 37 °C down to the edge of moderate hypothermia at 33 °C in the example survival situations discuss so far in this unit. Let’s use relatively common human mass of about 80 kg and the average specific heat of human tissue of 3470 J/(kg C°). [4]First we find the heat loss required for the temperature drop:
We know that in our example of a 10 mph wind and a -3 °C air temperature we found that a person with thin clothing and no space blanket experienced 1100 W of convective heat loss and 200 W of radiative heat loss for a total of 1300 W. If the person was shivering then their thermal power would be roughly 250 W. This person would have a 1150 W thermal power deficit, which means they lose 1150 Joules of thermal energy each second. Dividing the dangerous heat loss we calculated above by the thermal power deficit gives us the time required to lose that much heat:
Dividing the 900 s by 60 (s/min), we see that hypothermia would be reached in only 14 minutes. In reality, the rate of heat loss depends on the temperature difference so the rate of heat loss would not be constant, but instead it would slow a just bit as body temperature decreased. In our example case the 40.9 C° difference between the body temperature and environment temperature changed by only about 3 C° (seven percent). Ignoring this effect gives a reasonable approximation for the time until moderate hypothermia. The next two sections will address this approximation and allow us to calculate the time required for more significant temperature changes.
Rates of Body Temperature Change
The rate at which thermal energy is transferred out of the body depends on the difference in temperature between the body and the environment. As the body cools closer to the environmental temperature the rate will decrease. In the previous example we ignored this reality and assumed that the cooling rate was constant, which was reasonable because we only examined a very small temperature change. For our example situation we found that mild hypothermia would be reached in only twenty minutes. The graph below was produced by calculating the body temperature while accounting for a cooling rate that depends on the temperature difference. This was done using a numerical model:
- calculating a heat transfer rate for the initial body temperature due to both thermal radiation and forced convection
- using that heat transfer rate to calculate the amount of heat transferred over a relatively short time interval
- using the amount of heat transferred to calculate a resulting reduction in body temperature
- calculating a new body temperature by subtracting the reduction in body temperature
- repeat 1-5 until temperature was well beyond survival temperature, keeping track of the temperatures and times to make the graph
We see that the time to mild hypothermia is actually more like 30 mins. We also see that severe hypothermia could set in after less than an hour and the minimum survivable temperature could be reached in under two hours. For the purpose of these calculations we assumed a thermal power of 250 W while shivering, and that shivering stops when the body reaches 30 °C, at which point thermal power returns to 100 W. We also assumed the that thermal power dropped to zero when body temperature reached 21 °C.
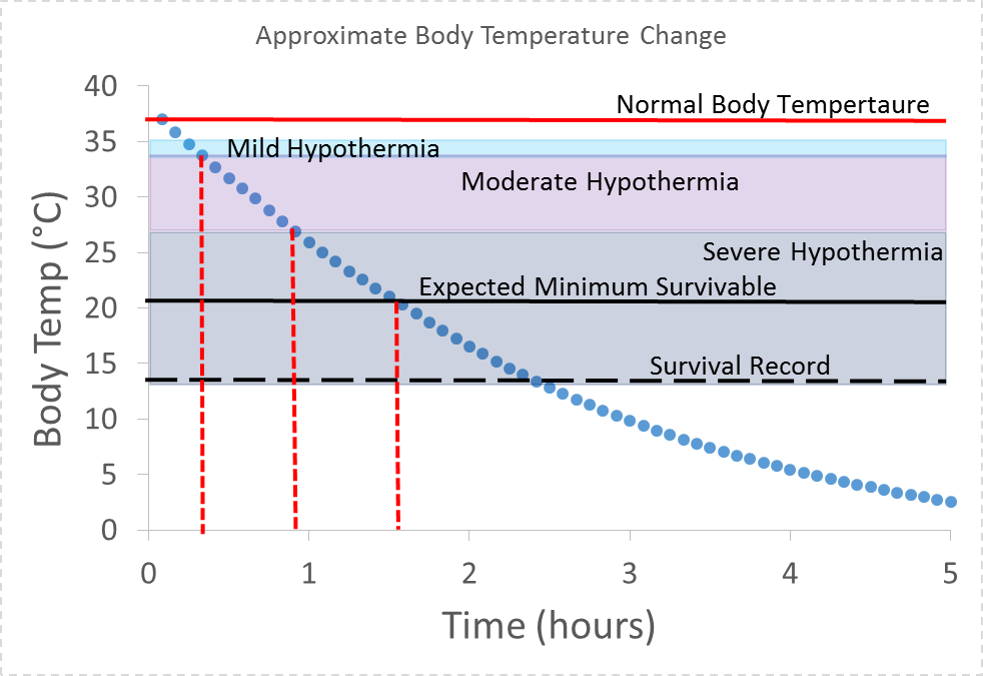
Approximate body temperature vs. time for an 80 kg person in 25 °F air temperature and 10 mph wind (-3 °C , 4.5 m/s). For the purpose of these calculations we assumed a thermal power of 250 W while shivering, that shivering stops at 30 °C at which point thermal power returns to 100 W, and that thermal power dropped to zero below 21 °C. Minimum survivable body temperature and record low body temperature survived were found at “How Cold Can a Body Get” by Ali Venosa, Medical Daily and “Frozen Alive” by Peter Stark, Outside Magazine.
Modeling how body temperature changes with time under different insulation and temperature conditions allows forensic investigators to measure a body’s temperature and work backwards to determine the time at which body temperature started to drop from normal. In this way time of death can be determined (unless of course the person was hypothermic or hyperthermic before death).
- Adapted from "Web-based hypothermia information: a critical assessment of Internet resources and a comparison to peer-reviewed literature" by M Spencer, Jeremy & Sheridan, Scott, Perspectives in public health, 135(2) · February 2014 ↵
- "Nutritional Needs In Cold And In High-Altitude Environments: Applications for Military Personnel in Field Operations" byAndrew J. Young, Michael N. Sawka and Kent B. Pandolf, National Center for Biotechnology Information, National Institutes of Health ↵
- OpenStax, College Physics. OpenStax CNX. Nov 8, 2018 http://cnx.org/contents/031da8d3-b525-429c-80cf-6c8ed997733a@14.4 ↵
- Engineering ToolBox, (2001). [online] Available at: https://www.engineeringtoolbox.com [Accessed 27 1 2019] ↵
The condition of having a body temperature well below the normal range.
Electromagnetic radiation spontaneously emitted by all objects with temperature above absolute zero.
transfer of heat due to the movement of fluid molecules driven by external factors other than thermal expansion.
Increase in rate of heat loss from objects that are warmer than air caused by the flow of air across the object surface.
rate at which chemical potential energy is converted to thermal energy by the body, batteries, or heat engines. Also, rate at which thermal energy is converted to electrical energy by a thermal power plant.
A material property that determines the amount of energy required to raise the temperature one mass unit of the material by one temperature unit.
The amount of energy required to raise the temperature of an object by one temperature unit.
a measurement of the amount of matter in an object made by determining its resistance to changes in motion (inertial mass) or the force of gravity applied to it by another known mass from a known distance (gravitational mass). The gravitational mass and an inertial mass appear equal.
An amount of thermal energy transferred due to a difference in temperature.
a rough value obtained without making a measurement by using prior knowledge and assumptions.
