60 The Laws of Motion
Newton’s Second Law
Early in this unit we found that The Law of Conservation of Momentum is equivalent to Newton’s First Law of Motion. Also, just in the previous chapter we saw that Newton’s Third Law of Motion is a direct result of combining Momentum Conservation + the Impulse Momentum Theorem (or vise versa). It may feel as though we have skipped the Second Law of Motion, but actually we have already been using it in secret. For example, at in the previous chapter we wanted to solve for the force applied to Jolene as she turned around so we started with the Impulse-Momentum Theorem and divided both sides time interval that the force was applied.
(1) ![]()
Stopping there we might have recognized that ![]() is exactly the definition of the average acceleration so we could make the replacement:
is exactly the definition of the average acceleration so we could make the replacement:
(2) ![]()
Written in this form, the impulse-momentum theorem is known as Newton's Second Law of Motion: the net external force on a system is equal to the system mass multiplied by the system acceleration. Notice that for the same net force, a larger mass must experience a smaller acceleration, meaning it will change its motion more slowly. Newton’s 2nd Law allows us to define mass as the measure of how much inertia a system exhibits. Also notice that Newton's First Law of Motion is hiding inside of the Second Law because any non-zero mass must have zero acceleration when the net force is zero.
Reinforcement Activity
Locomotion With Newton’s Laws of Motion
Locomotion can be understood in terms of Newton’s Laws of Motion. A body will move with a constant velocity until it experiences a net force (Newton’s First Law). A change in body motion is achieved by initiating muscle contraction in order to apply a force against another object, such as the floor or the wall. The other object then applies an equal and opposite force against the body (Newton’s Third Law). That equal and opposite force acting on the body adds together with all of the other forces on the body to determine the net force, which then causes an acceleration that depends on the the body mass according to Newton’s Second Law.
Examples
The astronaut in the video above starts out in static equilibrium relative to the space station. Then she pushed against the wall. The resistance of the wall to being deformed caused it to apply a normal force back on her. That unbalanced force destroyed her state of static equilibrium, overcame her inertia, and caused her velocity to change relative to the station. This example is a unique form of locomotion, but all locomotion depends on this same process of pushing on an object in order receive a push back form the object.
Reinforcement Exercises
Reinforcement Exercises
Jumping
Everyday Example: Jumping
When a person stands still on flat ground, they are in static equilibrium and the normal force pushing up from the ground is equal to their weight. In order to jump, the muscles of the leg contract to push down against the floor. This downward push results in an equal upward normal force from the floor, so that now the normal force is greater than body weight a there is an upward net force. Now with an upward net force, the body will experience an upward acceleration. The following graph of the normal force on person was created by jumping and landing on a force plate, which is essentially a extra-tough digital scale that records the normal force that it provides over time.
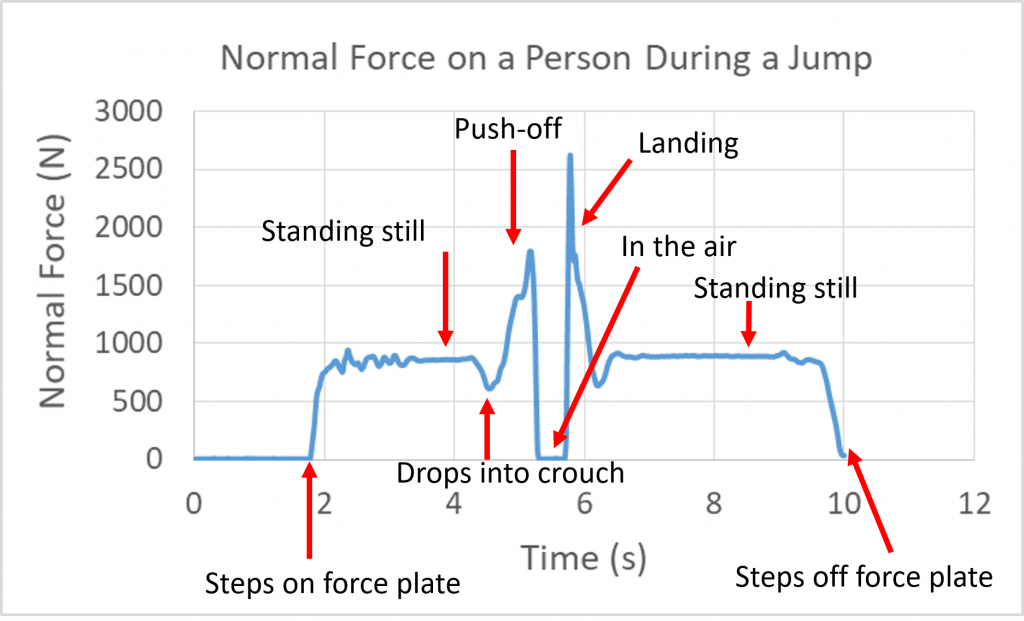
First the jumper steps on the force plate and it reads their weight of about 800 N. Then the plate reading dips a couple hundred Newtons because the upward normal force is reduced as they drop down into a crouch, which makes sense because they must accelerate downward to drop down. Next the force peaks to near 1700 N they push off hard to stop their downward motion and initiate upward motion. Throughout this stage the normal force is greater than the weight in order to create this upward acceleration. The normal force drops to zero as the body leaves contact with the ground. While in the air gravity provides the net downward force so the acceleration is downward, and the body’s upward velocity slows. (After leaving the ground the acceleration is –g= –9.8 m/s/s). The body eventually turns around as the upward velocity reaches zero, and then begins to move back toward the ground. Landing requires an upward acceleration to stop the downward velocity, so a large upward normal force of over 2500 N is produced. The jumper is attempting a “soft landing” and so continues into a crouching position during landing, which causes another couple hundred Newton dip in the normal force at the end of landing. Finally, the normal force equals weight again after landing is complete. Upcoming chapters will talk more about “soft landings” and other methods of injury prevention.
Check out this simulation to see how forces combine to create net forces and accelerations:
the change in momentum experienced by system is equal to the net force on the system multiplied by the amount of time that force is applied
The net force on a system is equal to the system mass multiplied by the acceleration
An object will not change it's motion unless acted upon by an external force.
the total amount of remaining unbalanced force on an object
a measurement of the amount of matter in an object made by determining its resistance to changes in motion (inertial mass) or the force of gravity applied to it by another known mass from a known distance (gravitational mass). The gravitational mass and an inertial mass appear equal.
the state being in equilibrium (no unbalanced forces or torques) and also having no motion
the outward force supplied by an object in response to being compressed from opposite directions, typically in reference to solid objects.
a quantity of speed with a defined direction, the change in speed per unit time, the slope of the position vs. time graph
the force of gravity on on object, typically in reference to the force of gravity caused by Earth or another celestial body
the change in velocity per unit time, the slope of a velocity vs. time graph