77 Dissipation in the Body

Preventing Injury During a Fall

X-Ray image showing a fractured clavicle (collar bone). Though this particular fracture occurred during a car accident, clavicle fractures are a one of the most common injuries resulting from falls. “Falls with serious injury are consistently among the Top 10 sentinel events reported to The Joint Commission’s Sentinel Event database […] with the majority of these falls occurring in hospitals. Every year in the United States, hundreds of thousands of patients fall in hospitals, with 30-50 percent resulting in injury. “Injured patients require additional treatment and sometimes prolonged hospital stays that increase medical costs by an average of 14,000 USD.” [footnote]"Preventing falls and fall-related injuries in health care facilities" by Sentinel Event Alert, The Joint Commission[/footnote] of Image Credit: Clavicle Fracture Left uploaded by Majorkev via Wikimedia Commons

In the previous chapter we learned how energy dissipation caused by the drag force affects the fuel efficiency of people and vehicles. We also learned that dissipation by the drag force makes skydiving safer by limiting the fall speed. In similar fashion, the mechanical efficiency of the body and other machines is limited by dissipation of energy, but those same dissipation mechanisms can be used to prevent injury by reducing impact forces during collisions.

Everyday Examples: Landing after a Jump

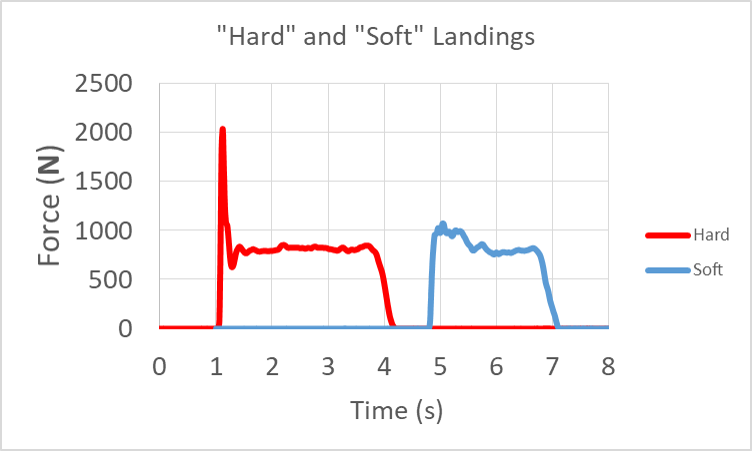
When a person impacts the ground and comes to a stop after a fall, then negative work is done to transfer their kinetic energy into thermal energy, or dissipate the energy. Bending the knees allows that dissipation work to occur within the muscles and and tendons over a long distance.  Landing rigid causes the dissipation to occur over a much shorter distance, and thus higher force, and more of the dissipation occurs within the joints (bones and ligaments). The force vs. time graphs show the normal force applied to a person when landing on one foot after stepping off from a 0.1 m height as seen in the GIF above. The graph on the left was the more rigid leg landing (it didn’t feel good) and the graph on the right was a bent-knee landing. Notice that the stiff-legged “hard” landing nearly doubled the peak force applied to the body.

A person steps off a small platform onto a force plate and on one foot with a stiff leg. The same person then steps off again and bends their leg as they land.
Stiff and bent-leg landings that produced the forces recorded in the graphs below.

 

Force vs. time curves: Stiff-leg hard-landing curve starts at zero then spikes to 2000 N for roughly 0.2 s before returning to a constant value near 800 N (bodyweight). Bent-leg, soft-landing starts at zero, jumps to 1000 N, creating a rounded bump roughly 0.4 s wide before returning to roughly 800 N and remaining constant.
Force vs. time data for a stiff-legged landing (red) and crouching landing (blue).

Dissipation (eccentric) Efficiency

Relatively little chemical potential energy is used to provide eccentric muscle tension (muscle tension while the muscle elongates) necessary for negative work. In fact, the negative work done can be larger than the chemical energy spent, which would produce a dissipation efficiency that was greater than 100%. However, the efficiency would be negative because the work is negative. [1].

In addition to dissipation work done by muscles, the tendons will store kinetic energy as elastic potential energy during impact, but if that energy is not released quickly then it dissipates to thermal energy.  Overall the body works to ensure that the maximum of amount of kinetic energy is dissipated during impact so that the objects stick together instead of bouncing off each other. That type of collision is called perfectly inelastic.  As we will see in the next chapter, bouncy collisions tend to increase the impact forces and likelihood of injury. Therefore, dissipating energy and minimizing bounce are the primary design goals of many safety systems like climbing ropes and crumple zones.

Concentric Efficiency

Compared to their eccentric efficiency, the muscles are much less efficient at performing activities that require concentric work, such as running or walking. During those activities we want collisions between our feet and the ground to be more elastic so that more kinetic energy is conserved rather than transferred to thermal energy. In that case our muscles will use less chemical potential energy to do the concentric work needed to replace the kinetic energy. If your body could somehow conserve 100% of the initial kinetic energy then you would bounce back at the same speed you had before the collision, without any muscle input at all, in which case we would say the collision was elastic. Elastic collisions are not possible in reality, but your body does achieve some bounce while walking or running, so the collisions are not perfectly inelastic either, they are just inelastic.

Everyday Example: Energy transfers in a climbing fall

Climbers define the fall-factor as the ratio of fall distance to rope available for stretch during the catch.  The maximum possible fall factor is 2, which corresponds to the rope being tied directly to the last anchor point so the total free-fall distance is twice the length of rope available. Climbing ropes are made to meet specific safety standards the require the rope to be stretchy, or “dynamic” enough that the force applied to an 80 kg climber will be less than 12,000 N for a fall factor of 2[2]. Keep in mind, that is still about 15x body weight for the 80 kg person!https://youtu.be/BHQ9pWEG9dE?t=55

A 65 kg rock climber is 4 m above their last anchor piece and falls. They will fall a total distance of 8 m before the rope begins to come tight and catch their fall. The rope stretches and springs back so they end up with just 0.5 m of stretch in the rope, sitting 8.5 m below their high point. Overall, how much mechanical energy is dissipated to thermal energy?

Modeling the rope stretch as a spring will require that we find the spring constant. We will do that with Hooke’s Law:

(1)   \begin{equation*} F = kd \end{equation*}

We want to know k so we should divide both sides by d to get

(2)   \begin{equation*} k = \frac{F}{d} \end{equation*}

We know that after the fall the weight of the climber just hanging there maintains 0.5 m of stretch in the rope and the weight of the climber is F_g = mg. Entering these values we can find k:

(3)   \begin{equation*} k = \frac{(65\,\bold{kg})(9.8\,\bold{m/s/s})}{0.5\,\bold{m}} = 1274\,\bold{N/m} \end{equation*}

Now we start with conservation of energy, including the change in elastic potential energy.

(4)   \begin{equation*} 0 = \Delta KE_i + \Delta PE_g + \Delta PE_s + \Delta TE + \Delta PE_c \end{equation*}

The system will include the climber, the earth, and the rope.

  • We will assume the work done by air resistance is negligible.
  • The climber will not be doing any work, so \Delta PE_c =0.
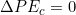  • The climber starts and ends at rest, so \Delta KE_i = 0

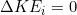
(5)   \begin{equation*} 0 = 0 + \Delta PE_g + \Delta PE_s +\Delta TE \end{equation*}

The change in gravitational potential energy for the final overall height change of -8.5 m can be calculated using \Delta PE_g = mg\Delta h

(6)   \begin{equation*} mg\Delta h = (65\,\bold{kg})(9.8\,\bold{m/s/s})(-8.5\,\bold{m/s/s}) = -5414.5\,\bold{J} \end{equation*}

The change in elastic potential energy for the final overall stretch of 0.5 m can be calculated using \Delta PE_s = \frac{1}{2}k(d)^2.

(7)   \begin{equation*} \frac{1}{2}k(d)^2 = \frac{1}{2}(1274\,\bold{N/m})(0.5 \bold{m})^2 = 159.25\,\bold{J} \end{equation*}

Entering these values into the conservation of energy equation:

(8)   \begin{equation*} 0 = -5414.5\,\bold{J} + 159.25\,\bold{J} +\Delta TE \end{equation*}

Isolating the thermal energy change:

(9)   \begin{equation*} \Delta TE = 5414.5\,\bold{J} - 159.25\,\bold{J} = 5255.25 \,\bold{J} \end{equation*}

The large majority of the energy was converted to thermal energy in the rope, so the rope has a high dissipation efficiency. This conversion does work to reconfigure the internal structure of the rope on a microscopic level, essentially causing microscopic damage that can add up over several falls. For this reason climbing ropes are rated for a certain number of falls before they need to be retired. The dissipation of energy is critical to many types of safety equipment.

The maximum force on the climber from the rope occurs when the rope is maximally stretched. At this moment the climber is momentarily at rest before the rope springs back, so none of the potential energy lost is stored as kinetic energy in that moment. If no energy was converted to thermal energy then all of the energy would become elastic potential energy, requiring a longer stretch distance to store all of the energy, and a longer stretch distance corresponds to a larger peak force applied to the climber by the rope (more force is required to stretch the rope a greater distance).

Additionally, without energy dissipation the rope would act like a spring, effectively making this an elastic collision. In that case the rope would bounce back up, pulling the  person’ back up from the harness with it while their legs, upper body, arms, and head are still moving downward due to inertia. This mismatch direction of motion leads to a greater chance of injury, as we will see in the next chapter.

Check out this simulation that allows you to visualize the transfer of energy in a falling mass caught by a spring. If you choose the energy option, attach the mass to the spring and drop it you will see how energy is transferred between gravitational, kinetic, and elastic energy. If you turn up the damping, which leads to dissipation, you will see how thermal energy increases and how the “bounce” is affected by dissipation.

  1. Menard MR, Penn AM, Lee JW, Dusik LA, Hall LD. Relative metabolic efficiency of concentric and eccentric exercise determined by 31P magnetic resonance spectroscopy. Arch Phys Med Rehabil. 1991 Nov;72(12):976-83. PMID: 1953321 ↵
  2. "UIAA Safety Standards" by UIAA. ↵
definition

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Body Physics 2.0 Copyright © by Lawrence Davis is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.

Share This Book